Проценко Ніна Федорівна, викладач правових дисциплін, спеціаліст вищої категорії Унавчально-методичному посібнику висвітлюються комплексно питання про закон
| Вид материала | Закон |
- Маляренко Світлана Олексіївна, спеціаліст вищої категорії, «старший учитель». «Нестандартні, 102.6kb.
- В. М. Захарова Використання інтерактивних методів навчання на урок, 682.45kb.
- Заступник директора з навчально-виховної роботи, вчитель математики вищої категорії,, 1763.48kb.
- Програма для вищих медичних навчальних закладів І-ІІ рівнів акредитації за спеціальністю, 2244.39kb.
- Вданій роботі подано методичні рекомендації, щодо використання методу проектів у курсі, 231.92kb.
- Програма вступного іспиту на базі освітньо-професійної програми підготовки молодшого, 194.52kb.
- Кияниця Ніна Віталіївна викладач української мови та літератури вищої категорії Тема,, 153.54kb.
- Довідка про підсумки проведення міських предметних олімпіад, 318.23kb.
- Формування ужиткових компетенцій при викладанні хімії Ряшина С.І., викладач вищої категорії,, 2216.75kb.
- Узгоджено: затверджую, 594.17kb.
5.3. Розподільні (диз'юнктивні) судження
Розподільними (диз'юнктивними) судженнями називаються судження, утворені із простих, за допомогою поєднання їх логічним сполучником "або".
Розрізняють два види розподільних суджень: розподільно-виключаючі (судження строгої диз'юнкції) та єднально-розподільні (судження слабкої диз'юнкції).
Розподільно-виключаючим називається таке судження, в якому ознаки, виражені предикатами, виключають один одного. Ці судження виражаються сполучником "або". Позначають цей сполучник знаком
 . Наприклад: "Попереднє розслідування закінчується або припиненням справи, або відданням звинувачуваного під суд".
. Наприклад: "Попереднє розслідування закінчується або припиненням справи, або відданням звинувачуваного під суд".Структура розподільно-виключаючого судження може бути записана так: ,S є Р1 або Р2 ... або Рп, або А
 В.
В.Розподільно-виключаючі судження виражають знання про те, що предмету думки може належати тільки якась із ознак, виражена предикатами, і не можуть належати усі можливі ознаки одночасно.
Розподільно-виключаючі судження будуть істинними тільки тоді, коли одне із суджень, що до нього входить, буде істинне, а решта — хибними. Якщо ж усі вихідні судження істинні або всі хибні, то й розподільно-виключаюче судження хибне.
У вигляді таблиць це записується так:
-
А
В
А В
В
і
і
X
і
X
і
X
і
і
X
X
X
Тут А і В — вихідні судження, а А
 В — складне розподільно-виключаюче судження.
В — складне розподільно-виключаюче судження.Отже, у двох випадках (у 2 і 3-му), складне судження строгої диз'юнкції (A
 В)є істинним , коли одне є істинним ,коли просте судження істинне, а друге хибне, коли обидва вихідні судження істинні, або обидва прості судження хибні.
В)є істинним , коли одне є істинним ,коли просте судження істинне, а друге хибне, коли обидва вихідні судження істинні, або обидва прості судження хибні.Єднально-розподільним судженням називається таке розподільне судження, в якому суб'єкту може належати не тільки один, а й усі перелічені предикати. Ці судження виражаються сполучником "або". Позначають цей сполучник знаком V. Наприклад: "Переховування може виражатися у прихованні злочину, а також засобів та знарядь скоєння злочину, або слідів злочину або предметів, здобутих злочинним шляхом". Сполучник послабленої диз'юнкції "або", за допомогою якого у цьому судженні предикати ("переховування злочинця", "знаряддя та засобів скоєння злочину", "слідів злочину", "предметів, здобутих злочинним шляхом"), означають, що суб'єкту судження ("переховування") може належати тільки якийсь один із цих предикатів, але можуть належати одночасно і всі названі предикати. Переховування може виразитися, наприклад, тільки у переховуванні злочинця, а може полягати у переховуванні злочинця, знаряддя і засобів здійснення злочину, слідів злочину та предметів, здобутих злочинним шляхом, одночасно.
Сполучник "або" і розділяє ознаки предмета, відділяє їх один від одного і допускає можливість поєднання ознак, їх суміщення. Цим єднально-розподільні судження відрізня-ються від розподільно-виключаючих суджень строгої диз'юнкції.
Формула єднально-розподільного судження така: S є Р1, або Р2, ... або Рп, або А V В.
Єднально-розподільне судження буде істинним, коли хоча б одне із простих суджень, які його утворюють, є істинним, а хибним тоді, як усі прості судження, котрі його утворюють, хибні.
Таблиця істинності для цих суджень така:
-
А
В
А V В
і
і
і
і
X
і
X
і
і
X
X
X
Із цієї таблиці видно, що єднально-розподільне судження "А V В" істинне у перших трьох випадках, а саме: 1) коли А і В істинні; 2) коли А істинне, а В хибне; 3) коли А хибне, а В істинне, і є хибним тільки тоді, коли обидва судження, що його утворюють (і А, і В), хибні.
Слід мати на увазі, що граматично єднально-розподільні судження у юридичному законодавстві і правовій науці виражаються не тільки сполучником "або", а й іншими сполучниками і словами — "оскільки", "також", "так", а також за допомогою коми.
5.4. Логічні сполучники та їхнє табличне визначення
5.4.1. Поняття про таблицю істинності
Точний смисл логічних сполучників визначається у логіці висловлювань за допомогою матриць, які називаються таблицями істинності.
Число рядків у таблиці істинності визначається за таким правилом: число рядків таблиці — 2", де п — це число різних пропозиційних змінних, що входять до формули, а 2 — це кількість логічних значень: «істина» й «хиба».
Так, наприклад, якщо формула складається з однієї про-позиційної змінної, то рядків у її таблиці істинності буде
2і = 2.
| №№ | Р |
| 1 | і |
| 2 | X |
Якщо до формули входять дві пропозиційні змінні, то її таблиця істинності буде складатися з 22 = 4 рядків.
| №№ | Р | q |
| 1 | і | і |
| 2 | і | X |
| 3 | X | і |
| 4 | X | X |
До стовпців таблиці істинності входять усі підформули досліджуваної формули. Так, наприклад, таблиця істинності для формули р q повинна мати такий вигляд:
| №№ | Р | Я | р 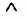 q q |
| 1 | і | і | |
| 2 | і | X | |
| 3 | X | і | |
| 4 | X | X | |
Спираючись на отримані знання, що стосуються побудови таблиць істинності, спробуємо тепер визначити основні логічні сполучники.
5.4.2. Заперечення, його умови істинності
Розглянемо два простих висловлювання:
(1) Київ розташований на Дніпрі.
(2) Невірно, що Київ розташований на Дніпрі.
Позначимо перше висловлювання пропозиційною змінною р, тоді друге висловлювання можна символічно записати як ~ р (читається «Невірно, що p»).
Перше із цих двох висловлювань буде істинним, тобто воно відповідає дійсності. Друге висловлювання навпаки буде хибним, бо в ньому заперечується той факт, який виражено у першому висловлюванні.
Тепер проаналізуємо другу пару простих висловлювань:
(1) Київ розташований на Волзі.
(2) Невірно, що Київ розташований на Волзі.
Перше з цих двох висловлювань буде хибним, бо у дійсності той факт, який у ньому описується, не існує. Якщо перед цим висловлюванням поставити сполучник «невірно, що...», тоді з його допомогою стає можливим заперечити той факт, який у ньому описується. В зв'язку з цим друге висловлювання, в якому було здійснене заперечення, може бути оцінене як істинне.
Таким чином, логічний сполучник «заперечення» творить із істинного висловлю-вання хибне, а із хибного — істинне.
Ці факти виражаються в таблиці істинності заперечення таким чином:
| №№ | А | ~А |
| 1 | і | X |
| 2 | X | і |
У природній мові, в тому числі і в правових контекстах, виразу «~ А», крім «невірно, що А», можуть відповідати також вирази «не-A», «А не має місце», «А хибне» тощо.
Наприклад, у статті 11 «Поняття злочину» Кримінального кодексу України: «Не є злочином дія або бездіяльність, що хоч формально і містить ознаки будь-якого діяння, передбаченого кримінальним законом, але через малозначність не являє суспільної небезпеки» логічний сполучник «заперечення» застосовується двічі. В обох випадках він виражається за допомогою частки «не».
Наприклад:
«Відень — столиця Австрії».
«5x5 = 50».
Вдавшись до операції заперечення, ми перетворимо істинне висловлювання на хибне («Хибно, що Відень — столиця Австрії), а хибне в істинне («Хибно, що 5x5 = 50»).
5.4.3. Кон'юнкція, її умови істинності
Розглянемо таке висловлювання:
«На вулиці холодно і йде дощ».
Це складне висловлювання, яке складається з двох простих:
(1) «На вулиці холодно».
(2) «На вулиці йде дощ».
Його формула може бути записана так: р q (читається «р і q»). Це висловлювання буде істинним лише тоді, коли обидва простих висловлювання, які входять до його складу, будуть істинними, тобто, якщо на вулиці дійсно холодно та йде дощ.
Якщо на вулиці холодно, але дощ не йде, тобто, якщо перше просте висловлювання є істинним, а друге — хибним, тоді їхня кон'юнкція найімовірніше буде оцінена як хибна.
Аналогічно кон'юнкція буде хибною, якщо виявиться, що на вулиці йде дощ, але стоїть тепла погода.
Нарешті, якщо ні перше, ні друге просте висловлювання не відповідатиме дійсності, тоді складне висловлювання також не буде відповідати дійсності і виявиться хибним.
Таким чином, кон'юнкція буде істинною лише в тому випадку, коли всі її складові висловлювання будуть істинними. Вона визначається хибною тоді, коли хоча б одне із складових висловлювань буде хибним.
Ці факти виражаються в таблиці істинності кон'юнкції таким чином:
-
№№
А
В
А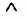 В
В
1
і
і
і
2
і
X
X
3
X
і
X
4
X
X
X
Виразу «А В» у природній мові, а також у юридичному законодавстві та правовій науці, крім «А і В», можуть відповідати також вирази: «А разом із В», «Як А, так і В», «А у той час, як В», «В, хоча і А», «Не лише А, але й В», «А, а також В», «А, В» та інші.
Наприклад, у статті 2 «Підстава кримінальної відповідальності» Кримінального кодексу України: «Ніхто не може бути визнаний винним у вчиненні злочину, а також підданий кримінальному покаранню інакше як за вироком суду й відповідно до закону» логічний сполучник «кон'юнкція» застосовується двічі. У першому випадку він виражається словами «а також», у другому — сполучником «й».
5.4.4. Диз'юнкція, умови істинності
У межах логіки висловлювань розрізняють слабку (не-строгу) диз'юнкцію і сильну (строгу) диз'юнкцію.
Слабка (нестрога) диз'юнкція
Розглянемо таке висловлювання: «Ця людина — юрист або спортсмен». Це складне висловлювання, яке складається з двох простих:
(1) «Ця людина — юрист».
(2) «Ця людина — спортсмен».
Його формула може бути записана як: р V q (читається «р або q»).
Це висловлювання може бути оцінене як істинне лише у тих випадках, коли:
• ця людина є і юристом, і спортсменом;
• ця людина є юристом, але не є спортсменом;
• ця людина не є юристом, але є спортсменом. Хибним це складне висловлювання буде лише тоді, якщо ця людина не є ні юристом, ні спортсменом.
Узагальнюючи вищенаведені випадки, можна зробити висновок про те, що диз'юнкція буде істинною лише тоді, коли хоча б одне із складових висловлювань буде істинним. Вона визнається хибною, якщо всі висловлювання, які до неї включаються, будуть хибними.
Ці факти можуть бути представлені в таблиці істинності слабкої (нестрогої) диз'юнкції таким чином:
-
№№
А
В
АVВ
1
і
і
і
2
і
X
і
3
X
і
і
4
X
X
X
З цієї таблиці видно, що сполучник «або» вживається тут у нестрого розмежувальному смислі — «А або В, чи обидва разом». Тому він і має назву — «слабка (нестрога) диз'юнкція».
Виразу «А V В» у природній мові та правових контекстах, крім звичайного «А або В», відповідають також вирази: «А чи В, або обидва разом», «А і/чи В», «А, якщо не В» тощо. Наприклад, у статті 19 «Осудність» Кримінального кодексу України: «Не підлягає кримінальній відповідальності особа, яка під час вчинення суспільно небезпечного діяння була в стані неосудності, тобто, не могла усвідомлювати своїх дій або керувати ними внаслідок хронічної душевної хвороби, тимчасового розладу душевної діяльності, слабоумства чи іншого хворобливого стану» диз'юнкція вживається чотири рази. У першому випадку вона представлена сполучником «або», у другому та третьому — за допомогою коми, у четвертому — сполучником «чи».
Сильна (строга) диз'юнкція
На відміну від слабкої (нестрогої) диз'юнкції сильна (строга) диз'юнкція передбачає використання сполучника «або» в строго розмежувальному смислі — «А або В, але не обидва разом». Для неї в логіці висловлювань вводиться новий символ — «
 ».
».Розглянемо таке висловлювання:
«Ця людина народилася в Києві або Львові».
Це складне висловлювання, складається з двох простих:
(1) «Ця людина народилася в Києві».
(2) «Ця людина народилася у Львові».
Його формула може бути записана як: р
 q (читається «або Р, або q»).
q (читається «або Р, або q»).Це висловлювання може бути оцінено як істинне тільки в тому випадку, якщо одне з простих висловлювань буде істинним, а друге — хибним.
Якщо ж обидва простих висловлювання виявляться одночасно істинними, тоді їхня диз'юнкція з необхідністю буде оцінена як хибна, бо неможливо одночасно народитися в двох містах.
Хибною строга диз'юнкція буде й у тому випадку, коли всі прості висловлювання, які її складають, виявляться хибними, тобто, якщо людина, про яку йдеться у складному висловлюванні, не народилася ні в Києві, ні у Львові.
Таким чином, сильна (строга) диз'юнкція буде істинною лише в тому випадку, коли логічні значення висловлювань, які входять до її складу, не збігаються, тобто, якщо одне з висловлювань є істинним, тоді друге — повинне бути хибним. Хибною строга диз'юнкція буде у тих випадках, коли логічні значення висловлювань, які входять до її складу, збігаються: вони або є істинними, або є хибними.
Ці факти можуть бути представлені в таблиці істинності сильної (строгої) диз'юнкції таким чином:
-
№№
А
В
А В
В
1
і
і
X
2
і
X
і
3
X
і
і
4
X
X
X
Виразу «А
 В» у природній мові та в правових контекстах можуть відповідати вирази: «А або В, але не обидва разом», «або А, або В», «чи А, чи В», «А, крім випадку, якщо В», «іноді А, В» та інші.
В» у природній мові та в правових контекстах можуть відповідати вирази: «А або В, але не обидва разом», «або А, або В», «чи А, чи В», «А, крім випадку, якщо В», «іноді А, В» та інші.Наприклад, у висловлюванні: «Злочин може бути здійснений або умисно, або з необережності» логічний сполучник «сильна (строга) диз'юнкція» виражається словами «або..., або...».
