Методика вивчення нумерації І арифметичних дій в 3-му класі. Методика вивчення табличного множення І ділення
| Вид материала | Книга |
СодержаниеПисьмові прийоми додавання і віднімання в концентрі “Тисяча”. |
- Лекція №11. Тема: Методика вивчення багатоцифрових чисел, 89.49kb.
- План Причини виділення першого десятка в окремий концентр. Підготовчий період до вивчення, 81kb.
- Уроків математики у 4 класі, 308.95kb.
- Зміст та методика вивчення кінематики гармонічних коливань, 233.3kb.
- Методика вивчення художньої культури північноамериканського культурного регіону, 527.82kb.
- Методика діагностики рівня інтелекту (впровадження психолого-педагогічної системи диференційованого, 19.44kb.
- Презентація навчального посібника «Література модернізму: художній стиль, методика, 42.75kb.
- Методичні рекомендації щодо вивчення географії у 9 класі 12-тирічної школи, 138.88kb.
- Методика проведення позакласних занять з математики. Методика розв’язування задач, 28.16kb.
- Відбулась Всеукраїнська нарада «Вивчення художньої культури та естетики в 11 класі, 19.1kb.
Для того, щоб дізнатися про загальну кількість десятків в числі, треба закрити в ньому 1 цифру справа.
| Число | Всього | ||
| | сотень | десятків | одиниць |
| 400 | 4 | 40 | 400 |
| 530 | 5 | 53 | 530 |
| 378 | 3 | 37 | 378 |
Для того, щоб дізнатися загальне число сотень в числі, треба справа закрити 2 цифри.
Далі учні знайомляться з випадками віднімання на підставі десяткового складу числа: 345 – 300, 345 – 40, 345 – 5.
Пам’ятка
Додавання і віднімання на підставі десяткового складу числа.
- Визначаю десятковий склад
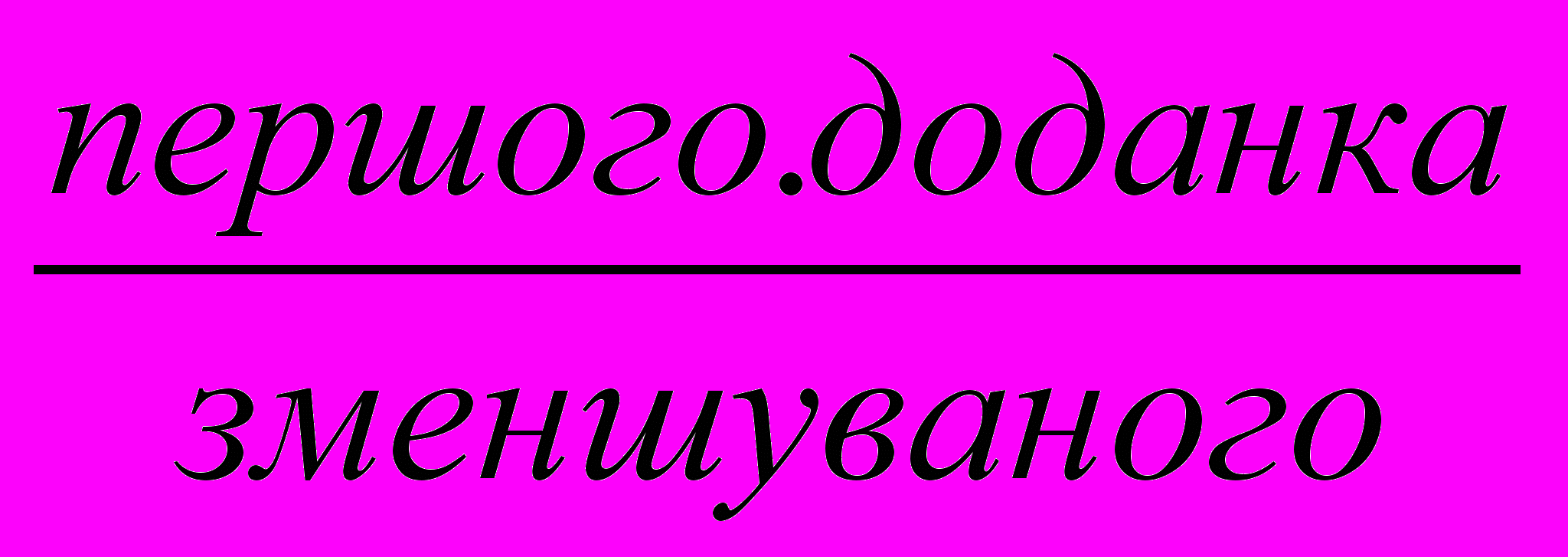 .
.
- Визначаю десятковий склад
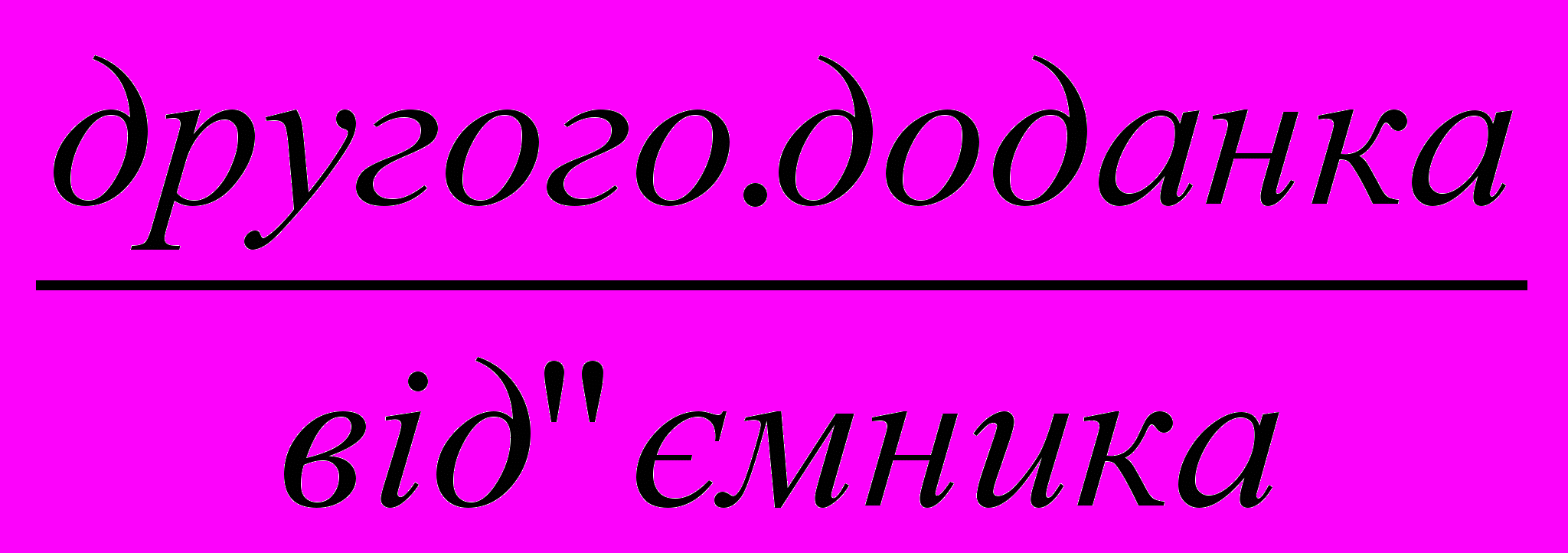 .
.
- Читаю приклад з словами “було”, “
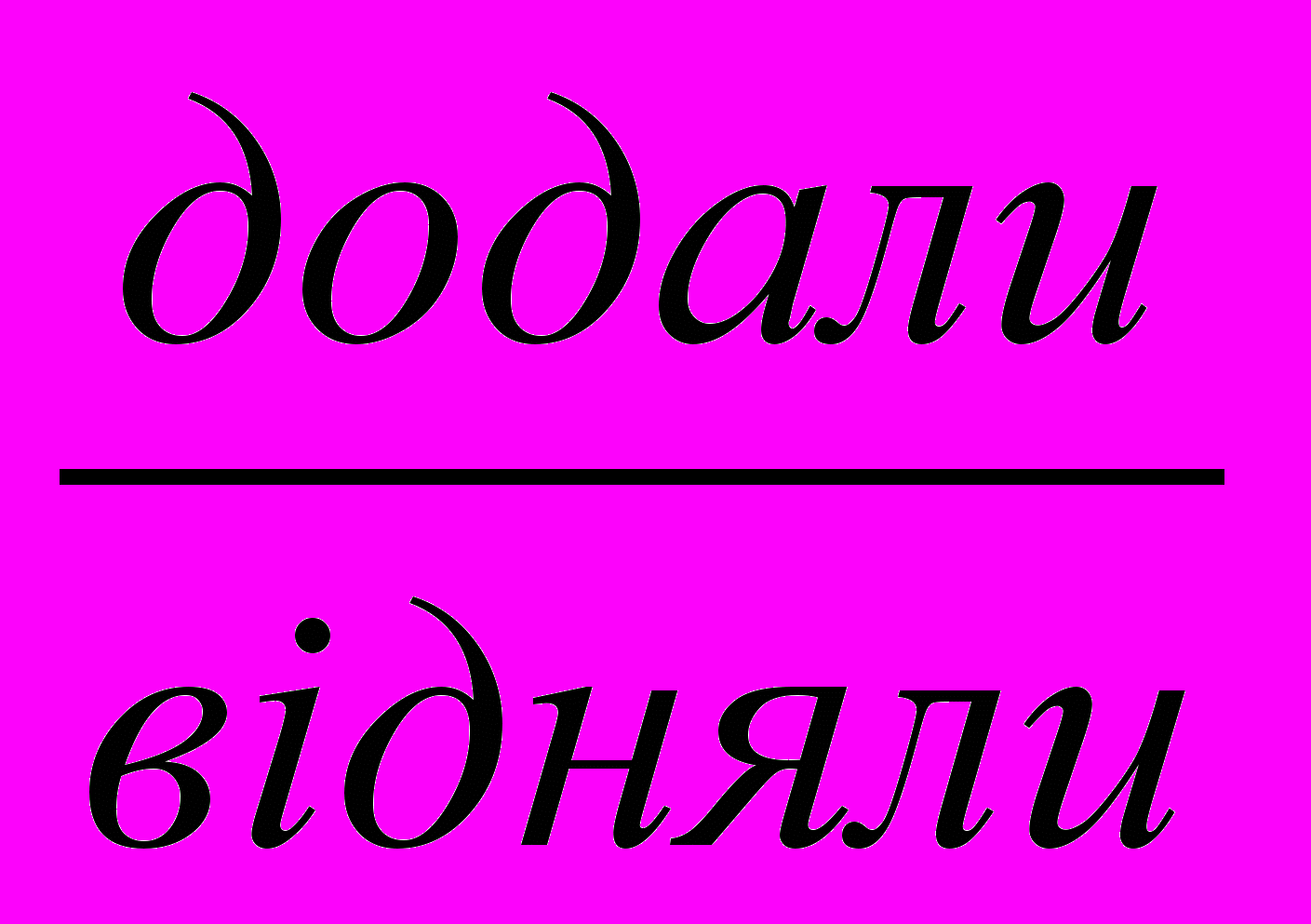 ”, “Отримали”.
”, “Отримали”.
- Записую ( читаю) відповідь.
Наприклад, 853 – 50:
- 853 – це 8 сотень, 5десятків та 3 одиниці;
- 50 – це 5 десятків.
- Було 8 сотень 5 десятків та 3 одиниці , відняли 5 десятків, отримали 8 сотень і 3 одиниці – це число 803.
- 8
 53 – 50 = 803.
53 – 50 = 803.
Знання з нумерації чисел в межах 1000 закріплюються і систематизуються при вивченні теми “Міри довжини і маси”.
Методика вивчення додавання і віднімання в межах 1000.
Усні прийми додавання і віднімання в межах тисячі.
Прийоми обчислювань, починаючи з концентру “Сотня” поділили на усні і письмові. Ці прийоми схожі тим, що їх запис повинен здійснюватися письмово. Але усні прийоми записуються в рядок і починаються обчислення з найвищого розряду, а письмові записуються у стовпчик і починаються обчислення з нижчого розряду. Методичною помилкою є запис у рядок, а обчислення у стовпчик і навпаки.
В результаті вивчення усних прийомів додавання і віднімання учні повинні вірно виконувати ці дії в межах 100, робити їх перевірку; усно виконувати додавання і віднімання в межах 1000 у тих випадках, які призводяться до дій в межах 100.
Таким чином, при вивченні додавання і віднімання трицифрових чисел ведеться також й робота по формуванню навиків усних обчислювань в межах 100.
Розглядання усних приймів додавання і віднімання в межах 1000 починається з розглядання цих дій з круглими числами на підставі відомого дітям способу укрупнення розрядних одиниць:
200 + 700 = 2 с. + 7 с. = 9с. = 900 800 – 300 = 8с. – 3 с. = 5 с. = 500
Спочатку розглядаються випадки без переходу через розряд, а потім й з переходом через розряд:
60 + 90 = 6д. + 9д. = 15д.=150 120 – 30 = 12д. – 3д. = 9д. = 900
Далі діти виконують додавання круглих трицифрових чисел способом порозрядного додавання без переходу через розряд:

 520 + 340 = 500 + 20 + 300 + 40 = 800 + 60 = 860
520 + 340 = 500 + 20 + 300 + 40 = 800 + 60 = 860500+20 300+40
 470 - 320 = 400 + 70 – 300 – 20 = 100 + 50 = 150
470 - 320 = 400 + 70 – 300 – 20 = 100 + 50 = 150



400+70 300+20
Висновок: сотні

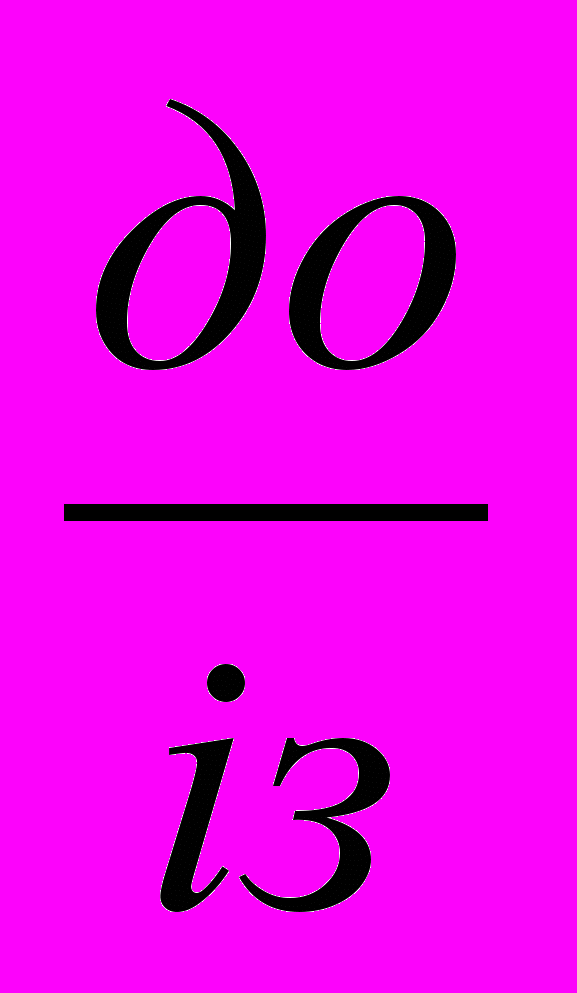 сотень, а десятки
сотень, а десятки  десятків.
десятків.  Розглядаються випадки додавання і віднімання до круглого трицифрового числа круглих сотень і круглих десятків, способом порозрядного додавання і віднімання:
Розглядаються випадки додавання і віднімання до круглого трицифрового числа круглих сотень і круглих десятків, способом порозрядного додавання і віднімання:430 + 500 = 400 + 30 + 500 = 900 + 30 = 930


400+30
 430 + 50 = 400 + 30 + 50 = 400 + 80 = 480
430 + 50 = 400 + 30 + 50 = 400 + 80 = 480
4
 00+30
00+30
 760 – 400 = 700 + 60 – 400 + 300 + 60 = 760
760 – 400 = 700 + 60 – 400 + 300 + 60 = 760700+60
 760 – 40 = 700 + 60 – 40 = 700 + 20 = 720
760 – 40 = 700 + 60 – 40 = 700 + 20 = 720700+60
Обчислення суми і різниці круглих трицифрових чисел пропонується рахувати чотирма способами:
1 спосіб – порозрядне додавання без переходу через розряд:


 560 + 230 = = 500 + 60 + 200 + 30 = 700 + 90 = 790
560 + 230 = = 500 + 60 + 200 + 30 = 700 + 90 = 790500+60 200+30
2 спосіб – додавання по частинах:
5
 60 + 230 = 560 + 200 + 30 = 760 + 30 = 790
60 + 230 = 560 + 200 + 30 = 760 + 30 = 790
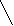
200+30
3 спосіб – укрупнення розрядних одиниць:
560 + 230 = 56д. + 23д. = 79д. = 790
4 спосіб – округлення:
560 + 230 = 600 + 230 – 40 = 830 – 40 = 790
1 спосіб – порозрядне віднімання без переходу через розряд:
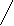
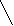
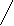
 870 - 260 = 800 + 70 – 200 – 60 = 600 + 10 = 610
870 - 260 = 800 + 70 – 200 – 60 = 600 + 10 = 610800+70 200+60
2 спосіб – віднімання по частинах:
8
 70 - 260 = 870 – 200 – 60 = 670 – 60 = 610
70 - 260 = 870 – 200 – 60 = 670 – 60 = 610

200+60
3 спосіб – укрупнення розрядних одиниць:
870 – 260 = 87д. – 26д. = 61д. = 610
4 спосіб – округлення:
870 – 260 = 870 – 300 + 40 = 570 + 40 = 610
У подальшому навчанні спочатку розглядаються випадки додавання до круглого трицифрового числа розрядного числа десятків, в результаті чого отримаємо розрядне число сотень:

 230 + 70 = 200 + 30 + 70 = 200 + 100 = 300
230 + 70 = 200 + 30 + 70 = 200 + 100 = 300200+30
А також розглядається віднімання з розрядного числа сотень розрядне число десятків:

 200 – 60 = 100 + 100 – 60 = 100 + 40 = 140
200 – 60 = 100 + 100 – 60 = 100 + 40 = 140100+100
Потім вивчається порозрядне додавання з переходом через розряд:
 380 + 590 = 300 + 80 + 500 + 90 = 800 + 170 = 970
380 + 590 = 300 + 80 + 500 + 90 = 800 + 170 = 970300+80 500+90
Далі вивчається віднімання з переходом через розряд з трицифрового круглого числа розрядного числа десятків двома способами:
1 спосіб – порозрядне віднімання з переходом через розряд:
 420 – 70 = 300 + 120 – 70 = 300 + 50 = 350
420 – 70 = 300 + 120 – 70 = 300 + 50 = 350

400+20
2 спосіб – віднімання по частинах:
4

 20 – 70 = 420 – 20 – 50 = 400 – 50 = 350
20 – 70 = 420 – 20 – 50 = 400 – 50 = 35020+50
Після цього вводиться віднімання круглих цифрових чисел з переходом через розряд способом віднімання по частинах:
6
 50 – 290 = 650 – 200 – 90 = 450 – 90 = 360
50 – 290 = 650 – 200 – 90 = 450 – 90 = 360200+90
6
 00 – 270 = 600 – 200 – 70 = 400 – 70 = 330
00 – 270 = 600 – 200 – 70 = 400 – 70 = 330200+70
Таким чином, всі усні способи обчислення, які були введені в концентрі “Сотня” реалізуються й в концентрі “Тисяча”. Зазначимо, що підготовча робота до вивчення способів обчислення в концентрі “Тисяча” здійснюється на аналогічних прикладах в межах 100.
Письмові прийоми додавання і віднімання в концентрі “Тисяча”.
Письмове додавання і віднімання спирається на знання розрядного складу чисел, засвоєння співвідношення розрядних одиниць, прочні знання табличних випадків додавання і віднімання в межах 10 та 20. Тому, перелічені знання і уміння повинні актуалізуватися на етапі підготовчої роботи до введення письмового прийму.
Зазначимо, що з письмовим прийомом додавання і віднімання учні познайомилися в межах 100, але в методиці математики передбачено мотивацію введення письмового прийому додавання і віднімання в межах 1000.
Для мотивації введення письмового прийму додавання трицифрових чисел пропонуємо учням для усного обчислення суми: 427 + 358 .До речі, такі випадки для усних обчислень учні не розглядали. Для визначення способу міркування користуємося аналогією ( користуємося відомим у дидактиці правилом-орієнтиром прийому аналогії):
- поставити мету міркування : визначити спосіб обчислення суми чисел 427 та 358;
- розглянути відомі властивості вивчає мого об’єкту: обидва доданки трицифрові числа, кожне трицифрове число можна подати у вигляді суми розрядних доданків, де окремо подані сотні, десятки та одиниці: 427 = 400 + 20 + 7, 358 = 300 + 50 + 8;
- згадати чи не зустрічався раніш схожий об’єкт: раніше ми додавали лише двоцифрові числа, кожне із яких подавалося у вигляді суми двох розрядних доданків;
- якщо зустрічається схожий об’єкт, то загадати всі його властивості: при додаванні двоцифрових чисел десятки додавалися до десятків, а одиниці до одиниць, а потім додавалися отримані суми; числа додавалися порозрядно, починаючи з найвищого розряду - десятків;
- порівняти властивості першого об’єкту і другого: двоцифрові числа містять лише два розряди – десятки і одиниці, а трицифрові числа містять три розряди: сотні, десятки та одиниці, при чому найвищій розряд - сотні.
- зробити висновок про наявність цих властивостей у першого предмету: двоцифрові числа додають порозрядно, тому трицифрові числа також можна додавати порозрядно, починаючи з найвищого розряду сотень: сотні додають до сотень, десятки – до десятків, одиниці – до одиниць, а потім додають отримані суми.
427 + 358 = ( 400 + 20 + 7) + ( 300 + 50 + 8) = ( 400 + 300) + ( 20 + 50) + ( 7 + 8) = 700 + 70 + 15 = 785
Таким чином, ми визначили спосіб обчислення суми трицифрових чисел, міркуючи за аналогією.
Учні з’ясовують, що таке міркування є дуже довге, і вчитель пропонує інший запис – стовпчиком і письмовий прийом міркування:
Пам’ятка
