Зміст та методика вивчення кінематики гармонічних коливань

Вид материала

Документы

Содержание Аналіз останніх досліджень та публікацій. Постановка завдання. Мета T секунд (див. рис.2), можна одержати іще один вираз для ω Перспективи подальших досліджень Зміст та методика вивчення кінематики гармонічних коливань Содержание и методика изучения кинематики гармонических колебаний

Подобный материал:

• Методика вивчення нумерації І арифметичних дій в 3-му класі. Методика вивчення табличного, 7801.16kb.
• Вплив звуків на живі організми. Розв’язування задач. 8 клас, 45.76kb.
• Лекція №11. Тема: Методика вивчення багатоцифрових чисел, 89.49kb.
• В. О., Марченко Т. М. Застосування задачного підходу до вивчення дисципліни “теорія, 99.83kb.
• Актуальні проблеми економічних коливань в україні. Анотація, 133.75kb.
• Методика діагностики рівня інтелекту (впровадження психолого-педагогічної системи диференційованого, 19.44kb.
• Презентація навчального посібника «Література модернізму: художній стиль, методика, 42.75kb.
• План Причини виділення першого десятка в окремий концентр. Підготовчий період до вивчення, 81kb.
• П/п Зміст заходів, 39.93kb.
• Зміст, 1336.5kb.

УДК 378.14

© 2005

Губін М. С., Фролова А. Ю.

ЗМІСТ ТА МЕТОДИКА ВИВЧЕННЯ КІНЕМАТИКИ ГАРМОНІЧНИХ КОЛИВАНЬ

Постановка проблеми. В процесі вивчення фізики майбутні інженери-педагоги оволодівають як базовими знаннями, так і навичками педагогічної майстерності. Тому для підготовки спеціалістів високого рівня потрібно удосконалювати не тільки зміст курсу фізики, а й методику його викладання, виділяти головне з великого обсягу навчального матеріалу, усувати формалізм. У цій статті йдеться про удосконалення змісту і методики вивчення кінематики механічних коливань, яка є основою для подальшого вивчення важливих розділів фізики та інженерних дисциплін.

Аналіз останніх досліджень та публікацій. Кінематику гармонічних коливань прийнято пояснювати на прикладі коливального руху проекції точки, яка рівномірно обертається по колу. На цій основі виникло невірне трактування кутової характеристики коливань ω. У коловому русі ω є кутовою швидкістю точки. При перенесенні цієї величини в рівняння гармонічних коливань їй надають нового змісту, визначаючи як “число коливань за 2π секунд”, що суперечить розмірності ω. Проте це визначення увійшло до багатьох посібників з фізики [1–3]. Крім того, для ω запроваджено три назви, дві з яких - “колова частота” і “циклічна частота” - не відображають суті цієї величини. Існуючі недоліки, на наш погляд, стали можливими через штучність методу, на основі якого було введено кутові характеристики коливань.

Постановка завдання. Мета статті – запропонувати методику вивчення кінематики гармонічних коливань, яка ґрунтується на результатах дослідів, проведених безпосередньо з тілами, що коливаються. Ця методика дає можливість легко усунути згадані непорозуміння і глибше та ясніше виявити фізичний зміст величин, якими характеризуються гармонічні коливання.

Досліди проводяться зі звичайним набором коливальних систем, при цьому обов'язково записують розгортку коливань, наприклад, за допомогою маятника з пісочницею (рис.1).

Р
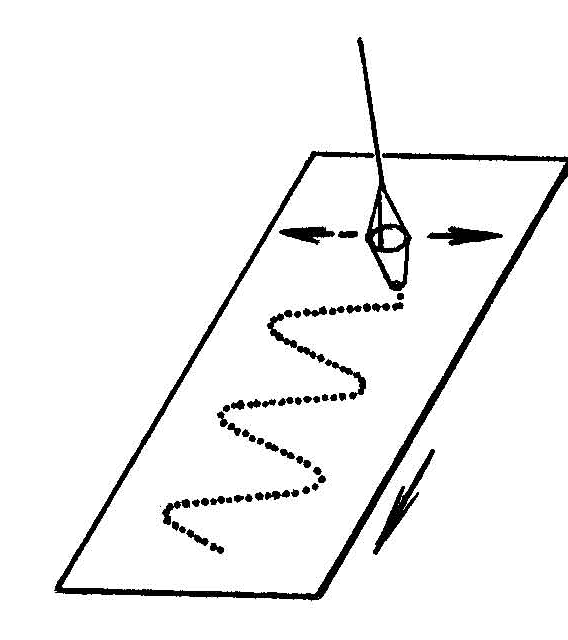
ис. 1. Схема одержання розгортки коливань маятника

Із дослідів можна зробити такі висновки:

• характерною ознакою коливальних рухів є їх повторення;
  
• повторення коливань відбувається через рівні проміжки часу;
  
• графік коливань має вигляд синусоїди.
  

Після цього з'ясовують, що повторюється у ході коливань. Під час руху тіла змінюються його зміщення x від положення рівноваги та напрям руху. Зміщення і напрям руху вкупі визначають миттєвий механічний стан коливного тіла. При цьому зміщення характеризується не тільки величиною, а й знаком. У ході коливань тіло проходить через неперервний ряд станів, періодично повертаючись до початкового. Отже, при коливаннях повторюються механічні стани тіла. Послідовність станів, після проходження яких тіло повертається в початковий стан, утворюють одне повне коливання або цикл (слово цикл у перекладі із грецької означає круг, круговорот). На графіку (рис.1) одному циклу відповідає одна хвиля кривої, тобто горб і западина.

Максимальне зміщення тіла від положення рівноваги називається амплітудою коливань А. Стани максимального зміщення візуально легко фіксуються, оскільки в них тіло на мить зупиняється, змінюючи напрям руху. Рух від одного стану максимального зміщення до другого і назад до першого є прикладом одного повного коливання (циклу). Зрозуміло, що початок відліку коливань можна вибрати від будь-якого іншого стану. Шлях, який проходить тіло у процесі одного повного коливання, дорівнює чотирьом амплітудам. Час одного повного коливання називається періодом коливань Т. Кількість коливань (або циклів), які тіло здійснює за одну секунду, називається частотою коливань ν .

Нехай за час t тіло здійснило N повних коливань. Тоді

T = t/N, (1)

ν = Ν/t, (2)

звідси випливає, що

T = 1/ν і ν = 1/T, (4)

тобто період і частота обернені одна по відношенні до другої величини.

Частота вільних коливань визначається властивостями коливної системи, в той час як амплітуда залежить тільки від початкових умов. Найпростішими коливання стають при малих амплітудах (причина цього з'ясовується при вивченні динаміки коливальних рухів); у подальшому розглядатимуться саме такі прості коливання.

Нашою задачею є знаходження залежності зміщення від часу. Рівняння, яке виражає цю залежність, називається кінематичним рівнянням коливань.

Із дослідів випливає, що для математичного опису коливань потрібна знакозмінна функція, вигляд якої зображається рис. 1. Звичайно, не кожна крива, що схожа на синусоїду, є синусоїдою. Але очевидно, що найпростіші коливання будуть описуватись і найпростішою функцією, тобто синусоїдою.

Н
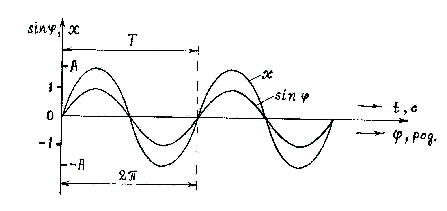
а рис.2 для порівняння наведено два графіки – графік залежності зміщення x від часу t для коливного тіла, наприклад, маятника (побудувати цей графік можна за даними розгортки коливань), і графік функції sinφ.

Рис. 2. Графік коливань і графік синусоїди

Оскільки цикл змін зміщення x повинен співпадати з циклом змін значення синуса, то масштаби на осі абсцис для часу t і для аргументу φ вибрано так, щоб період коливань тіла T секунд і кутовий період синуса 2π радіан співпадали. Як видно із рисунка, зміщення тіла змінюються пропорційно до змін синуса, тобто x ~ sinφ, а значення аргументу φ збільшується пропорційно до часу t, тобто φ ~ t. Оскільки при нульовому значенні синуса зміщення дорівнює нулю, при максимальному значенні синуса, що дорівнює одиниці, зміщення також стає максимальним і рівним А, а при sinφ = -1 зміщення x_max= -А, то очевидно, що у будь-який момент часу зміщення дорівнює добутку амплітуди і значення синуса:

x = Аsinφ. (5)

Позначивши коефіцієнт пропорційності між аргументом φ і часом t буквою ω, одержимо

φ = ωt. (6)

Величина ω, як видно із цього рівняння, дорівнює приросту аргументу φ за одну секунду і вимірюється в радіанах за секунду. Оскільки за одну секунду здійснюється ν коливань, яким на графіку відповідає така ж кількість кутових періодів 2π, то приріст аргументу за секунду, тобто ω, виразиться формулою

ω = 2πν. (7)

Величина ω, яка дорівнює добутку кута 2π і частоти коливань ν, називається кутовою частотою коливань.

Знаючи, що приріст аргументу φ на 2π радіан відбувається за T секунд (див. рис.2), можна одержати іще один вираз для ω:

ω = 2π/T. (8)

Коливання, що описуються функцією синуса, називають гармонічними коливаннями. На основі (5) і (6) рівняння гармонічних коливань записується у вигляді

x = Аsinωt. (9)

Із (9) випливає, що в початковий момент часу t = 0 зміщення тіла x = 0, тобто відлік часу починається від моменту проходження тілом положення рівноваги. Проте відлік часу приходиться починати і від інших моментів, наприклад, від моменту проходження тілом зміщення x₀, якому відповідає аргумент φ₀. Це значить, що аргумент синуса у загальному випадку слід записувати у вигляді суми чи різниці ωt і φ₀:

φ = ωt ± φ₀ . (10)

Якщо, наприклад, в початковий момент часу зміщення x₀ = А, то у відповідності з рівняннями (5) і (10) φ₀ = π/2, φ = ωt + π/2, і рівняння коливань набуває вигляду:

x = Аsin(ωt + π/2 ) = Аcosωt. (11)

Із цього прикладу випливає, що коливання описуються функцією косинуса тоді, коли відлік часу ведеться від моменту максимального зміщення тіла від положення рівноваги.

Рівняння гармонічних коливань дозволяє за відомим у даний момент станом тіла визначити аргумент φ і, навпаки, за відомим аргументом визначити миттєвий стан тіла, що коливається.

При порівнянні коливань двох однакових коливальних систем, наприклад, маятників, можливі такі ситуації:

• рухаючись в одному напрямку, маятники проходять через однакові стани одночасно, тобто їхні коливальні рухи нічим не відрізняються;
  
• при русі один із маятників раніше ніж другий проходить через положення рівноваги, через стан максимального зміщення і т.д., другий маятник, рухаючись за першим , ті ж стани проходить пізніше;
  
• у кожен момент часу маятники рухаються у протилежних напрямках – свої положення рівноваги вони проходять одночасно, але в протилежних напрямках, максимальні зміщення вони досягають одночасно, але ці зміщення протилежні за знаком і т.д.
  

Виразимо ці три фізичні ситуації математично:

x₁ = Аsinωt, x₂ = Аsinωt;

x₁ = Аsinωt, x₂ = Аsin(ωt – φ₀);

x₁ = Аsinωt, x₂ = -Аsinωt = Аsin(-ωt) = Аsin(ωt - π),

де x₁- зміщення першого маятника, а x₂ -другого.

Як бачимо, відмінності в коливаннях відображаються в рівняннях відмінностями тільки в аргументах синуса. В теорії гармонічних коливань за аргументом синуса закріпились назви: “фазовий кут”, “фаза”. Короткий термін “фаза” зручний, наприклад, тим, що дозволяє в лаконічній формі прокоментувати ситуації, описані вище трьома парами рівнянь, а саме: 1) коливання маятників за фазою співпадають; 2) коливання другого маятника за фазою відстають від коливань першого на φ₀; 3) коливання маятників за фазою протилежні (дійсно, аргументи синуса мають протилежні знаки). У цьому випадку можна також сказати, що коливання другого маятника за фазою відстають від коливань першого на π радіан.

Висновки. Найпростіші коливальні рухи характеризуються такими фізичними величинами, як зміщення x, амплітуда А, період T, частота ν. При вільних незатухаючих коливаннях із цих величин тільки зміщення змінюється з часом. Залежність зміщення від часу математично описується функцією синуса, із-за чого коливання називають гармонічними, при цьому до перелічених фізичних величин додаються іще і кутові величини - кутовий період 2π, кутова частота ω і фаза φ ( початковий кут φ₀ називають початковою фазою). Тепер очевидно, що термін “колова частота”, який нерідко застосовують до величини ω, є зайвим, а термін “циклічна частота” логічно було б застосувати не до кутової величини ω, а до частоти ν, яка показує скільки циклів (або коливань) здійснює коливне тіло за кожну секунду [4]. Проте досить залишити за величиною ω одну назву “кутова частота”, а ν називати просто частотою, як це зараз і прийнято.

На практиці доводиться мати справу з коливаннями різного ступеню складності, які не є гармонічними. Але і в цих випадках знання про гармонічні коливання необхідні, оскільки будь-які складні коливання математично можна виразити сумою певного набору гармонічних коливань. На цій основі успішно вирішуються як теоретичні, так і практичні задачі, пов'язані з коливальними процесами.

Перспективи подальших досліджень – застосування запропонованого вище підходу до вивчення фізики поширення гармонічних коливань в пружних середовищах.

Література

1. Сивухін Д.В. Общий курс физики. Т. I. Механика. -М.: Физматчит. МФТИ, 2002. -560 с.
   
2. Савельев И.В. Курс общей физики. Кн. 1. Механика.-М.: Астрель, АСТ, 2003.-336 с.
   
3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики. Т. 1. Механіка. Молекулярна фізика і термодинаміка.- К.: Техніка. 1999.- 536 с.
   
4. Хайкин С.Э. Физические основы механики. -М.: Физматиз, 1962. -772 с.
   

Губін М.С., Фролова А.Ю.

Зміст та методика вивчення кінематики гармонічних коливань

У статті запропоновано новий підхід до вивчення кінематики коливального руху, який дозволяє глибше розкрити фізичний зміст характеристики гармонічних коливань і усунути недоліки, що виникли на основі традиційного методу.


Губин Н.С., Фролова А.Ю.

Содержание и методика изучения кинематики гармонических колебаний

В статье предложен новый подход к изучению кинематики колебательного движения, позволяющий глубже раскрыть физический смысл характеристик гармонических колебаний и устранить недостатки, допущенные на основе традиционного метода.

N.S.Gubin, A.Y.Frolova

Content and methods of investigation of harmonic oscillations kinematics

In the paper there is suggested to study kinematics of oscillary motion that enables to reveal the physical notion of harmonic oscillations characteristics deeply and to eliminate the drawbacks of the traditional method.


Стаття надійшла до редакції 31.10.2005р.