Лекція №11. Тема: Методика вивчення багатоцифрових чисел

Вид материала

Лекція

Содержание Наприклад: 4256 4256 4256 4256 4256 4256 3 1254 - вивчається алгоритм (послідовність) дії множення. х42300 6 64 245 + 348 + 4360 - неповний добуток 522 Наприклад: х421 х316

Подобный материал:

• Нумерація багатоцифрових чисел. Множення І ділення багатоцифрових чисел на одноцифрове, 100.59kb.
• 31. 01. 2012 р. 2-а клас, 131.17kb.
• План Причини виділення першого десятка в окремий концентр. Підготовчий період до вивчення, 81kb.
• Програми для середньої загальноосвітньої школи. К.: Початкова школа, 2006 Богданович, 80.06kb.
• Лекція №1 Тема: Індоєвропейські мови. Техніка лінгвістичної реконструкції. Індоєвропейська, 365.7kb.
• Методика вивчення нумерації І арифметичних дій в 3-му класі. Методика вивчення табличного, 7801.16kb.
• Лекція 1 хф (лекція) Тема Загальні властивості неметалів, 1201.72kb.
• Зміст та методика вивчення кінематики гармонічних коливань, 233.3kb.
• Тема: Додавання та віднімання чисел у межах 10. Закріплення нумерації чисел у межах, 81.57kb.
• Вопросы к экзамену по курсу «Вычислительные системы, сети и телекоммуникации», 51.75kb.

Лекція № 11.

Тема: Методика вивчення багатоцифрових чисел.

Мета вивчення: навчити студентів методики вивчення нумерації невід'ємних чисел і арифметичних дій над ними у концентрі багатоцифрові числа

Література: Бантова М.О. та ін. Методика викладання математики у початкових класах. - К., 1989.

Богданович М.В. Методика вивчення нумерації і арифметичних дій в початковій школі. - К, 1990.

Клименченко Д.В. Збірник вправ з математики для початкових класів -К, 1987.

План

1. Зміст концентру багатоцифрових чисел.

2. Нумерація багатоцифрових чисел.

3. Додавання та віднімання багатоцифрових чисел.

4. Множення багатоцифрових чисел.

5. Ділення багатоцифрових чисел.

Опрацювання лекцій та додаткової методичної літератури.

1. Нумерацію багатоцифрових чисел і дії над ними виділено в окремий концентр тому, що нумерація чисел за межами 1000 (тисячі) має свої особливості: багатоцифрові числа утворюють, називають, записують, виходячи з поняття не тільки розряду, а й класу. Треба розкрити це найважливіше поняття нашої системи числення (десяткової). Арифметичні дії над багатоцифровими числами виконують з використанням як усних, так і письмових прийомів обчислення.

2. Основні завдання вчителя під час вивчення цієї теми:

• Сформувати поняття про нову лічильну одиницю - 1000 (тисячу), як одиницю 2 класу;
  
• Виходячи з поняття класу, навчити утворювати читати і записувати багатоцифрові числа;
  
• Узагальнити знання дітей про нумерацію цілих невід'ємних чисел.
  

1 етап. На підготовчому етапі до вивчення цієї теми треба закріпити знання дітей про співвідношення відомих їм розрядних одиниць, про десятковий склад трицифрових чисел, про натуральну послідовність чисел у межах 1000, про принципи записування трицифрових чисел. Наступний етап - це етап вивчення багатоцифрових чисел.

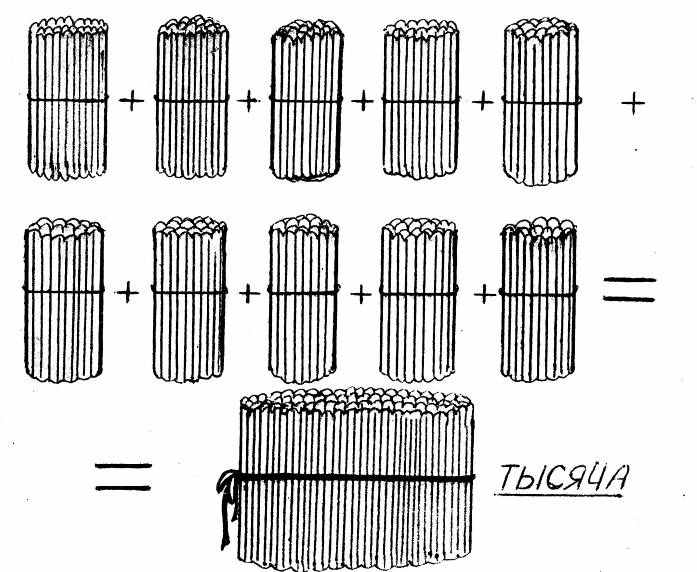
Вчитель пояснює, що 1000 можна лічити як прості одиниці (Ітис. 2 тис.) і групувати їх у десятки і сотні. Використовуючи рахівницю, лічать одиниці тисяч (відкладаючи їх на 4 дротинці знизу) до 10 тисяч, які замінюють одним десятком тисяч (відкладаючи на 5 дротині знизу), потім лічать десятки тисяч і, діставши десять десятків тисяч, замінюють їх 1 сотнею тисяч (відкладають на 6 дротині знизу), нарешті лічать сотні тисяч до 10 і замінюють 10 сотень тисяч 1 мільйоном (відкладаючи на 7 дротині знизу).

Утворення нових розрядних одиниць зафіксовують в записі: 10 од. тис = 1 дес. тис, 10 дес. тис. = 1 сот. тис, 10 сотень тисяч = 1 мільйону. Це допоможе дітям побачити схожість в утворені і назвах розрядних одиниць. Потім працюють з нумераційною таблицею, в якій позначено назви всіх розрядних одиниць і класів (перші 3 розряди - одиниці. десятки і сотні - утворюють 1 клас - клас одиниць; слідуючи 3 розряди - одиниці тисяч, десятки тисяч, сотні тисяч-утворюють 2 клас - клас тисяч: слідуючи 3 розряди - розряд одиниці мільйонів, десятки мільйонів, сотень; мільйонів утворюють 3 клас - клас мільйонів.....).

Так учні підходять до розміщення нескінченності натурального ряду чисел.

На наступному етапі переходять до закріплення знань і умінь учнів за допомогою різних тренувальних вправ.

3. Основне завдання вчителя під час вивчення цієї теми - узагальнити і систематизувати знання учнів про дії додавання і віднімання, закріпити навички усного +, -, виробити свідомі і міцні навички письмових обчислень + і -.

Підготовча робота до вивчення цієї теми починається ще при вивчені нумерації багатоцифрових чисел. Для цього насамперед повторюють усні прийоми + і - і властивості дій, на які вони спираються:

Наприклад: 8400 + 600 = 9000; 9800 - 700 = 9100 і т.д.

Потім повторюють письмові прийоми + і - трицифрових чисел 752

+ 246

переходячи на + і - багатоцифрових чисел 4652

+ 3246 і т.д.

Розв'язавши такі приклади, учні самостійно роблять висновки про те, що письмове + і - багатоцифрових чисел виконують так само, як і письмове + і - трицифрових чисел.

Далі вводять складніші випадки + і - , поступово збільшується кількість переходів через розрядну одиницю, включаються випадки -, коли у зменшуваному є нулі; потім додавання кількох додатків, а також + і - іменованих чисел

Наприклад: 4256 4256 4256 4256 4256 4256

⁺ 4123 ⁺4125 ⁺4145 ^-3123 ^-3196 ^-3127

_- 47450 _- 97000

6329 63254

Це все супроводжується поясненнями: + одиниці; + десятки; + сотні і т.д. (алгоритм + і -). Вивчаючи + і - багатоцифрових чисел приступають до вивчання + і - складених іменованих чисел, виражених метричними мірами, оскільки прийоми цих обчислень схожі. Є два способи + і - іменованих чисел.

1 спосіб: 12 т 647 кг 13 км 086 м

+ 5 т 384 кг - 8 км 265 м

17 т 1031 кг 4 км 821 м

18т 031кг

Цей спосіб економний щодо запису, добре ілюструє аналогію дій над абстрактними та іменованими числами, але деякою мірою важкий для дітей (пояснити чому).

2 спосіб обчислення над іменованими числами значно простіший , хоч і громоздкіший щодо запису.

Наприклад: 124 крб. - 78 крб. 50 коп. = 45 крб. 50 коп.

1крб. - 1000коп. 124 крб. = 12400 коп.

78 крб. 50 коп. = 7850 коп.(перетворення можна робити усно).

12400

7850

4550(коп.)


В кінці другого півріччя 4 класу вивчають + і - іменованих чисел, виражених мірами часу. Ці обчислення значно складніші, бо одиниці часу визначаються не десятковими численнями. На це спеціально звертають увагу дітей.

Наприклад: 13 год. 54 хв. 12 год. 34 хв.

+ 6 год. 46 хв. - 8 год. 56 хв.

19 год. 100 хв. 3 год. 38 хв. (шісткова

20 год. 40 хв. система числення)

Вправи на + і - іменованих чисел, виражених одиницями часу, з

невеликими числами треба виконувати усно, не записуючи обчислення стовпчиком.

4. Прийоми множення і ділення багатоцифрових чисел дуже різні і значно складніші, ніж прийоми + і - багатоцифрових чисел. Тому прийоми множення і ділення б/ц чисел вводяться по черзі, при цьому виділяють 3 етапи.

1 етап. Множення і ділення на одноцифрове число;

2 етап. Множення і ділення на двозначні, тризначні розрядні числа;

3 етап. Множення і ділення на двоцифрове і трицифрове число.

На кожному з етапі спочатку вивчають множення, а потім ділення. Поряд із множенням, ділення абстрактних чисел вивчають множення і ділення відповідних іменних чисел

Розглянемо спочатку перший етап множення. На підготовчому етапі повторюють:

1. Випадки множення з 1 і 0; 1•а = а; а • 1 = а; а • 0 = 0; 0 • а =0;

2. Розглядають множення розрядних чисел на одноцифрове 40 • 2; 400 • 2; 4000 • 2; 4 сот. • 2;

3. Множення двоцифрового числа на одноцифрове (на основі властивості множення суми на число).

13 • 4 = 40 + 12 = 52 , або (5+5+3)•4=52

Для ознайомлення учнів з письмовим множенням краще взяти такі приклади: 418 • 3 = 1254, або

_х 418

___ 3

1254

- вивчається алгоритм (послідовність) дії множення.

_х42300

6

253800

Після вивчення множення на одноцифрове число абстрактних чисел розглядають множення складених іменованих чисел, виражених метричними мірами.

Наприклад: 9 т 438 кг • 3 = 28 т 314 кг, або

_х9 т 438 кг _х9438

3 3

28 т 314 кг 28314 (кг)

2 етап - це множення на розрядні числа.

Це множення на 10, 100, 1000, а потім 40, 400, 4000 тут використовують властивості множення числа на добуток.

Наприклад: 14 • 60 = 14•(6 • 10) = 84 • 10 = 840.

Після усного множення на розрядні числа вводять письмове множення на ці числа.

Наприклад: 546 • 30; _х546

30

16380, і вивчають алгоритм множення.

Особливої уваги заслуговують приклади, у яких обидва множники закінчуються нулями.

Наприклад: 20 • 30 = 600; 400•50 = 20000; 8000•70 = 560000

_х7800 _х1320

10 4000

3 етап - це множення на 2 цифрове і трицифрове число.

Роботу починають з усного множення.

Наприклад: 16 • 12 = 16 • (10 + 2) = 160 + 32 = 192 (множення суми на число)

Потім пропонують важчий випадок.

87•64 = 87•(60 + 4) = 5568

1) ₊87 2) ₊ 87 3) ₊5220

60 4 348

5220 348 5568, після розв'язку вчитель показує коротший запис і дає відповідне пояснення (алгоритми).

_х87 _х872

64 245

+ 348 + 4360 - неповний добуток

522 3488

5568 1544

193.640 - повний добуток

Після розгляду загальних випадків множення на двоцифрове і трицифрове число вводяться окремо випадки: множення чисел, у записі яких на кінці і в середині є нулі.

Наприклад: _х421 _х316

305 240

₊2105 ₊1264

1263 632

128405 75.840

При множенні складених іменованих чисел йде заміна на прості іменовані числа і виконується дія, як над абстрактними числами, (натуральними)

Наприклад: 7 м 64 см • 37 = 282м268 см

_х764

37

₊ 5348

2292

28268 (см)

5. Ділення багатоцифрових чисел. Як було вже сказано ділення б/ц чисел вивчають паралельно з множенням в 3 етапи. Після вивчення множення на одноцифрове число розглядають ділення на одноцифрове число (1 етап), потім після вивчення множення на розрядні числа вивчають ділення на розрядні числа (2 етап), далі після вивчення множення на двозначні, трьохзначні розрядні числа число вивчають ділення на 2 цифрове і 3 цифрове число (3 етап). Письмове ділення на одноцифрове число починають вивчати з повторення випадків ділення з 1 і нулями.

• А : а = 1; а : 1 = а; 0 : а = 0; ( а: 0 не можливості ділення на нуль.).
  
• повторення ділення з остачею: 25 : 3 = 8 (ост. 1).
  
• У процесі вивчення письмового ділення використовують властивість ділення суми на число 38 : 2 = (10 + 20 + 8): 2 = 19
  

3963 : 3 = (3000 + 900 + 60 + 3) :3 (якщо ділимо кожен розряд).

На 1 етапі: письмове ділення починають з ділення на 1 цифрове число.

(25 дес. перше неповне ділене) (8дес.) і 1 одиниця у остачі

25 3

24 8

1(ост.)

2916 6 1) перше неповне ділене 29 сотень....

- 24 486 2) ділимо сотні.....

51 3) перевіряємо....

- 48 4) ділимо десятки....

36 5) перевіряємо....

- 36 6) ділимо одиниці...

0 7) перевіряємо...



12282 6

12 2047 Випадок коли у частці "нуль"

_-
Дві сотні на 6 не діляться, так, щоб у частці були сотні. Тому у частку записуємо “0” (нуль)
28

24

_-42

42

0

Далі розглядаємо ділення на круглі десятки.

2 етап.

Наприклад: 12750 30

12 425 1 неповне ділене 127 сот.

75

60

150

150

0

3 етап - це ділення на 2 цифрове число і 3 цифрове число.

552 23 315 63

46 24 315 5

_92 0

92

0 цифру у частці знаходять у наслідок проб

300 : 60 = 5 раз.

Прийоми ділення на трицифрове число аналогічні прийомам ділення на двоцифрове число.

37294 643

3215 58

_ 5144

5144

0

Алгоритм.

1) називаємо компоненти ділене 37.294, дільник 643

2) 1 неповне ділене 3729 - у частці буде 2 цифри

3) шукаємо перше число 37 : 6, пробуємо 6 - багато, беремо по 5 = 30

4) шукаємо 2 цифру 51:6 пробуємо по 8 приблизно 48

5) частка 58.

На цьому етапі вивчають прийоми ділення іменованих чисел, виражених у метричних мірах. Ділення зводиться до заміни іменованого числа простим і до виконання дії над відповідними абстрактними числами.

28 грн.: 35 = 80 коп. 57 грн. 60 коп.: 48 коп. = 120

2800 135 5760 1 48

280 80 (коп.) 48 120

0 96

96

0




Запитання і завдання до теми:

1. В чому полягає підготовка до вивчення багатоцифрових чисел?
   
2. Система, методи і прийоми вивчення нумерації багатоцифрових чисел.
   
3. Місце, зміст та методика запровадження елементів алгебраїчної пропедевтики при вивченні багатоцифрових чисел.
   
4. Методичні особливості вивчення додавання і віднімання багатоцифрових чисел.
   
5. Методика вивчення додавання і віднімання іменованих чисел.
   
6. Послідовність і методика вивчення множення та ділення багатоцифрових чисел (абстрактних та іменованих).
   
7. Особливості додавання і віднімання іменованих чисел, виражених мірами часу.
   

8. Розглянути публікації з журналів та газети “Початкова школа”, “Начальная школа”, “Розкажи онуку”, “Освіта” (висвітлення актуальних проблем заданої теми). Форма роботи – обговорення повідомлень.