Освоивших образовательные программы основного общего образования, организуемой территориальными экзаменационными комиссиями Калининградской области в 2008-2009 учебном году Калининград
| Вид материала | Методические рекомендации |
- Администрация владимирской области департамент образования прика, 401.39kb.
- Прика з, 165.18kb.
- Калужская область, 207.13kb.
- Приказ 23. 09. 2010 №2447 г. Саратов, 2042.38kb.
- Аналитическая справка по итогам проведения государственной (итоговой) аттестации обучающихся,, 1088.56kb.
- Верховного Совета Российской Федерации, 1992, n 30, ст. 1797; Собрание закон, 85.26kb.
- Инструктивно-методическое письмо «О преподавании русского языка в общеобразовательных, 2788.3kb.
- Публичный доклад, 1564.51kb.
- Целевая программа калининградской области «Содействие занятости населения Калининградской, 635.09kb.
- Программа подготовки выпускников 9-х классов моу «Октябрьская средняя общеобразовательная, 421.48kb.
56,35% девятиклассников подтвердили свою годовую отметку, 3,17% повысили, 40,48% - понизили. Этот факт говорит о том, что хотя данная форма экзаменационной работы еще не опробирована массово в регионе, но объективное оценивание достижений учащихся преобладает.
Структура вариантов экзаменационной работы
Таблица 5
| | Часть 1 | Часть 2 | Часть 3 |
| Общее число заданий – 15 | 8 (53 %) | 5 (33%) | 2 (13%) |
| Тип заданий и форма ответа | №1-№4 с выбором ответа; №5- №8 с кратким ответом | № 9- № 12 с кратким ответом; № 13 с развернутым ответом | №14, №15 с развернутым ответом |
| Уровень сложности | Базовый | Повышенный | Высокий |
| Предполагаемый процент верных ответов | 50-90% | 20-50% | Менее 20% |
В части 1 работы проверялись умения решать типичные задачи, применяя 1-2 геометрических факта и несложные вычисления. В частности, в ходе решения задач использовались:
- теорема Пифагора; формула площади треугольника;
- соотношение между величинами соответствующих центрального и вписанного углов.
- свойства отрезков касательных, проведенных из одной точки к данной окружности;
- свойства углов ромба;
- определение и свойство средней линии треугольника;
- признаки подобия треугольников и пропорциональность сторон треугольников;
- формула площади параллелограмма;
- определение и свойства равнобедренной трапеции;
Все задания базового уровня были представлены достаточно простыми задачами с решением в два шага, один из которых был весьма тривиальным. При выполнении заданий этой части работы учащиеся показали достаточно высокие результаты. Следует отметить, что задания с выбором ответа оказались легче, чем задания с кратким ответом. Только задача (№ 6) на подобие треугольников оказалась для 58 % учащихся, имеющих годовую отметку «удовлетворительно» и 30 % учащихся, имеющих отметку «хорошо» более трудной, несмотря на то, что она была дана в самой простой постановке. Этот материал традиционно хуже усваивается слабыми учащимися.
По задаче на нахождение площади параллелограмма (№ 7) в целом получен неплохой результат. Но 29,17% «троечников» и 33,8% «хорошистов» не знают формулу нахождения площади параллелограмма с использованием синуса угла между его сторонами.
В части 2 работы проверялись умения решать несколько более трудные задачи, чем задачи базового уровня, как правило, требующие применения 1-2 геометрических фактов в измененной ситуации. В ходе решения этих задач проверялись умения применять следующие геометрические факты:
- равносторонний треугольник и его свойства;
- определение медианы, биссектрисы угла треугольника;
- теорема Пифагора;
- теорема косинусов;
- площадь круга;
- определение и свойства параллелограмма;
- признаки параллельности прямых и свойства углов при параллельных прямых и секущей;
- признаки подобия треугольников и пропорциональность сторон треугольников;
- определение и свойства правильного многоугольника;
- скалярное произведение векторов.
Лучше всего учащиеся справились с задачей № 12, где необходимо было установить, какими из перечисленных свойств обладает параллелограмм и его виды. Это задание на знание и понимание изученных геометрических фактов позволяет проверить умение проводить рассуждение при решении задачи, обнаруживая возможности для их использования.
Несколько ниже, но тоже неплохие результаты получены по заданиям на скалярное произведение векторов (№9) и умение использовать свойства правильных многоугольников (№10) при решении задач. В задаче на векторы (с кратким ответом) требовалось найти скалярное произведение двух векторов с общим началом. Начало и конец одного вектора совпадали с вершинами равностороннего треугольника, а второй являлся либо медианой, либо биссектрисой треугольника. Только четверть девятиклассников, имеющих в году «удовлетворительно» и половина «четверочников» успешно решили эту задачу. Тема «Векторы» часто вызывает затруднения у учащихся, особенно, если речь идет не о прямом применении сведений о векторах. Заметим, что демоверсия экзаменационной работы содержала подобное задание, впрочем, как и задачу № 10.
Хуже всего девятиклассники справились с решением практико-ориентированной задачи (№ 11). Она была дана в нетипичной для школьного курса постановке и предполагала работу с текстом, связанным с измерениями на местности. Данные в этих задачах содержали десятичные дроби, причем в том случае, когда десятичных дробей в процессе решения появлялось больше, результаты выполнения задания были заметно ниже, что, видимо, связано с вычислительными ошибками. 91,33% учеников, успевающих на «три» и 76,01 % «хорошистов» не смогли правильно решить эту задачу. В то время как 100 % «отличников» выполнили ее верно.
Решение остальных задач повышенного уровня вызвало определенные трудности у многих учащихся.
В задаче на доказательство (с развернутым ответом) требовалось доказать два утверждения. Верное доказательство каждого из них оценивалось одним баллом. Для решения задач нужно было использовать свойства углов при параллельных прямых и секущей, признаки подобия треугольников и признак равнобедренного треугольника. Необходимо было грамотно записать доказательные рассуждения. 41,66% «троечников», 64,79% «четверочников» и 38,71 % «отличников» сумели доказать только одно утверждение, в то время как 61,28 % «пятерочников» выполнили задание полностью.
Это говорит о том, что задачи, в решении которых нужно применить несколько геометрических фактов и приемов в незнакомой ситуации, посильны только самым подготовленным и способным учащимся. Так 14 задачу группа «хорошистов» выполнила на 24 % хуже «отличников», хотя подобная задача присутствовала в демоверсии.
Последняя задача (ее полное и верное решение оценивалась тремя баллами) была ориентирована на проверку творческих возможностей выпускников основной школы. Ее решение требует поиска способа решения, состоящего из достаточно большого числа шагов, при этом необходимо проведение дополнительных построений и рассмотрение комбинации геометрических фигур.
«Через точку О пересечения продолжений боковых сторон трапеции ABCD проведена прямая, параллельная основаниям AB и CD. Эта прямая пресекает продолжения диагоналей DB и AC трапеции в точках M и N соответственно. Найдите площадь трапеции AMND , если площадь треугольника BOC равна 4, а площадь трапеции ABCD равна 96.»
С задачей не справились 100% учащихся. Это говорит о том, что даже для сильных учащихся задачи, требующие очень хорошей ориентации в свойствах геометрических фигур и большой самостоятельности мышления, представляют значительную трудность.
Диаграмма качества выполнения учащимися экзаменационной работы
Диаграмма 2
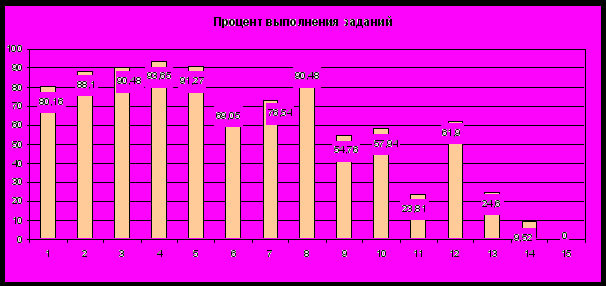
На оси абсцисс отмечены номера заданий, на оси ординат – выполнение соответствующего задания в процентах.
Как было сказано выше, учащиеся в целом показывают хорошие результаты при выполнении заданий базового уровня. С задачей № 6 справилось подавляющее большинство учащихся, получивших экзаменационную отметку «хорошо». Что касается решения практико-ориентированной задачи (№ 11) на вычисление числа саженцев цветов определенного вида на клумбе круглой формы, то у 66,07% учащихся, продемонстрировавших при выполнении всей работы хороший уровень математической подготовки, ее решение вызвало серьезные трудности. В числе причин неуспеха в ее решении можно выделить две основных.
Во-первых, подобных задач в учебниках и во многих дидактических материалах очень мало. Поэтому при выборе дидактических пособий (задачников, рабочих тетрадей, карточек и т.п.) следует обращать внимание на их наличие. Целесообразно также увеличить и общее число рассматриваемых на уроке задач, эффективно используя прием устного решения задач по готовым чертежам.
Во-вторых, для решения задач повышенного уровня нужно применить небольшое число геометрических фактов, но в такой ситуации, которую обычно называют измененной, т. е. в ситуации, не всегда отрабатываемой на уроках геометрии. Часть учащихся, даже усвоивших определенные элементы содержания, «не узнает» в представленной постановке задачи возможность применения этих элементов.
Выполнение заданий по вариантам (в %).
Таблица 6
| № задания | Уровень сложности | 945 | 946 | 947 | 948 | 953 | 954 | 955 | 956 |
| 1 | базовый | 80,76 | 83,33 | 73,08 | 85,19 | 85,71 | 80 | 60 | 83,33 |
| 2 | 88,45 | 87,5 | 96,15 | 81,48 | 100 | 80 | 80 | 83,33 | |
| 3 | 96,15 | 87,5 | 88,46 | 88,89 | 100 | 80 | 80 | 100 | |
| 4 | 88,46 | 100 | 96,15 | 96,30 | 100 | 60 | 80 | 100 | |
| 5 | 92,31 | 95,83 | 92,31 | 88,89 | 85,71 | 100 | 80 | 83,33 | |
| 6 | 69,23 | 79,17 | 50 | 85,19 | 57,14 | 60 | 40 | 83,33 | |
| 7 | 69,23 | 70,83 | 88,46 | 59,26 | 85,71 | 100 | 40 | 83,33 | |
| 8 | 92,31 | 87,5 | 92,31 | 88,89 | 71,43 | 100 | 100 | 100 | |
| 9 | повышенный | 53,85 | 54,17 | 69,23 | 51,85 | 57,14 | 60 | 20 | 33,33 |
| 10 | 69,23 | 54,17 | 46,15 | 70,37 | 42,86 | 60 | 60 | 33,33 | |
| 11 | 26,92 | 16,67 | 15,38 | 18,52 | 57,14 | 20 | 40 | 50 | |
| 12 | 76,92 | 66,67 | 50 | 51,85 | 100 | 40 | 40 | 66,67 | |
| 13 | высокий | 26,92 | 37,5 | 11,54 | 14,81 | 57,14 | 20 | 20 | 33,33 |
| 14 | 11,54 | 12,5 | 7,7 | 14,81 | 0 | 0 | 0 | 0 | |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Кол-во учащихся | 24 | 26 | 26 | 27 | 7 | 5 | 5 | 6 | |
Анализ выполнения частей работы по восьми вариантам показал значительный разброс в полученных результатах. Так, в варианте 953 с заданием 12 справились 100% учащихся, в вариантах 954-955 это же задание выполнили 40%.
Следующая таблица содержит данные о среднем балле учащихся, выполнивших работу.
Изменение результатов экзамена по отношению к годовой отметке, в зависимости от выполненного варианта
Таблица 7
| № варианта | Средний балл | «3» | «4» | «5» | Повыс. | Подтв. | Пониз. |
| 945 | 4,12 | 11,54 | 65,38 | 23,08 | 7,69 | 57,69 | 34,62 |
| 946 | 4 | 25 | 50 | 25 | 4,17 | 62,50 | 33,33 |
| 947 | 3,85 | 34,62 | 46,15 | 19,23 | 3,85 | 61,54 | 34,62 |
| 948 | 4,3 | 7,41 | 55,56 | 37,04 | 0 | 44,44 | 55,56 |
| 953 | 4,14 | 14,29 | 57,14 | 28,57 | 0 | 57,14 | 42,86 |
| 954 | 4 | 20 | 60 | 20 | 0 | 60,00 | 40,00 |
| 955 | 3,8 | 40 | 40 | 20 | 0 | 40,00 | 60,00 |
| 956 | 4 | 0 | 100 | 0 | 0 | 66,67 | 33,33 |
Неравномерное распределение результатов, не говорит о неравносильности заданий, размноженных в вариантах, а скорее подчеркивает, то, что тот или иной вариант выполняли более сильные учащиеся.
Распределение обучающихся по баллам
Таблица 8
| Всего: 126 чел. | ||||||||
| Баллы | 0-5 | 6-8 | 9-10 | 11-12 | 13-14 | 15-16 | 17 | 18-20 |
| Кол-во учащихся | 2 | 23 | 32 | 27 | 29 | 12 | 5 | 0 |
| (%) | 1,5 | 18,2 | 25,3 | 21,43 | 23,01 | 9,52 | 3,96 | 0 |
При получении учащимся 11-12 баллов за работу можно говорить о наличии у него достаточной подготовки для продолжения обучения на базовом уровне; 13-14 - на профильном (при соответствующей корректировке знаний), свыше 15 баллов - в профильных классах.
Методические рекомендации по подготовке к государственной (итоговой) аттестации выпускников IX классов общеобразовательных учреждений
(в новой форме) по геометрии
В ходе обучения геометрии необходимо обратить самое серьезное внимание на обеспечение усвоения всеми учащимися минимума содержания на базовом уровне.
Для решения этой проблемы следует в процессе обучения ставить посильные учебные задачи и добиваться их выполнения от всех учащихся. Понятно, что этап формирования базовых умений у менее подготовленных школьников займет больше времени, чем потребуется более подготовленным учащимся для усвоения материала на базовом уровне. Поэтому в арсенале учителя должны быть средства и методы, позволяющие обеспечить дифференцированный подход к учащимся, организовать для слабых учащихся возможность более длительной отработки умений в ходе решения простых задач, а для более сильных – достаточно быстрый переход к решению задач повышенного уровня.
Желательно при изучении каждой темы ознакомить учащихся с требованиями к обязательному уровню подготовки. Например, указать, какие задачи (в учебнике, дидактическом пособии) они должны уметь решать для получения удовлетворительной оценки. Можно предложить учащимся список таких задач, например, в качестве заданий для самопроверки достижения обязательной подготовки по теме.
Для того чтобы быстро и успешно справляться с решением задач повышенного уровня, необходимо помнить, что учащийся за короткое время должен проанализировать предлагаемую в задаче фигуру, распознать в ней опорную конфигурацию, установить связи между ее элементами: их взаимное расположение, метрические соотношения. Это возможно, если, выполняется ряд условий:
- формируются представления об опорных конфигурациях на протяжении всего процесса изучения курса геометрии;
- обращается внимание учащихся на такие конфигурации, решаются задачи на доказательство свойств соответствующих фигур, а также задачи на применение доказанных свойств;
- КИМы содержат такие задачи повышенного уровня, процент решения которых действительно соответствует предполагаемому диапазону решения. Если ни один из способных учащихся не смог решить задачу, хотя бы на один балл из трех возможных, то видимо, либо задача слишком сложная, либо недостаточное количество времени отводится на обдумывание решения.
Задачи высокого уровня сложности, как правило, в общеобразовательных классах на уроках решаются редко. Во-первых, самостоятельно найти путь решения для большинства учащихся – непосильная задача, а во-вторых, решение таких задач требует значительных временных затрат. Поэтому для наиболее сильных учащихся необходимо предусмотреть индивидуальные задания на дом или для работы в классе, которые выполняются по желанию ученика и поощряются оценками. Иногда сложные задачи можно рассматривать на уроке в качестве фронтальной работы с классом. В таком случае более сильные ученики должны быть заняты поиском решения, составлением плана решения задачи, а менее подготовленные учащиеся – выполнением и обоснованием отдельных шагов решения. При таком подходе пользу получат все ученики.
Большую роль в приобретении умений решать задачи, в которых применяются факты из разных разделов курса геометрии, играет обобщающее повторение, на которое выделяется учебное время в конце учебного года. Материал следует повторять «классифицировано», за основу классификации целесообразно принять вид фигуры (треугольники, четырехугольники, окружность и т.п.). При этом для каждого вида фигур рассматриваются все изученные в курсе способы вычислений (теорема Пифагора, теоремы синусов и косинусов, решение пропорций в подобных треугольниках, формулы площади и т.п.). В такую схему повторения естественным образом вписывается обобщающее рассмотрение свойств опорных конфигураций.
При проведении различных форм текущего контроля следует использовать задания, аналогичные заданиям ГИА-9.
Учителям математики следует внимательнее знакомиться с нормативными документами, определяющими экзамен в новой форме, обращать внимание не только на демонстрационный вариант, содержание спецификации и кодификатора, но и на методические письма ФИПИ об использовании результатов экзаменов в 2008 - 2009 г.г.
Методическую помощь учителю, обязательно принимаемую к сведению, могут оказать следующие материалы, размещенные на сайте ФИПИ:
- документы, регламентирующие разработку КИМ для ГИА по геометрии 2009 г. (кодификатор элементов содержания, спецификация и демонстрационный вариант экзаменационной работы);
- учебно-методические материалы для членов и председателей региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ выпускников 9-х классов 2009 г.;
- перечень учебных изданий, рекомендуемых ФИПИ для подготовки к экзамену.
ИСТОРИЯ
Анализ выполнения экзаменационной работы по истории в 2008/2009 учебном году
Экзаменационную работу по истории писали 47 учащихся из 9 муниципалитетов области и одного образовательного учреждения регионального подчинения (Таблица 1).
Таблица 1.
| № | Муниципальное образование | Кол-во писавших работу |
| | Гвардейский район | 6 |
| | ГО «Г. Калининград» | 26 |
| | Гурьевский МР | 2 |
| | Зеленоградский район | 3 |
| | Неманский МР | 1 |
| | Полесский ГО | 2 |
| | Советский ГО | 1 |
| | Светловский ГО | 1 |
| | Черняховский МР | 3 |
| | Регион | 2 |
| | Итого | 47 |
Характеристика экзаменационных материалов.
Общее число заданий в работе 33. Работа состояла из 3-х частей.
Часть 1 (А) содержит 20 заданий с выбором ответа (один верный из четырех предложенных). С их помощью проверяется базовый уровень подготовки выпускников. Часть 2 (В) состоит из 7 заданий повышенного уровня сложности с кратким ответом. Часть 3 (С) включает задания высокого уровня сложности – задания для работы с документом и задание с открытым развернутым ответом.
Общи итоги контрольной работы.
Средний балл по итогам выполнения учащимися контрольной работы составил 3,39, что свидетельствует о достаточном уровне знаний учащихся по истории (Таблица 2).
Итоги по муниципалитетам
Таблица 2
| № | Муниципальное образование | Средний балл | % качества знаний | Подтвер-дили | Повы-сили | Пони-зили | % выполнения работы |
| | Гвардейский район | 2,5 | 0 | 16,7 | 0 | 83,3 | 33 |
| | ГО «Г. Калининград» | 3 | 15,4 | 27 | 4 | 69 | 44,4 |
| | Гурьевский МР | 3,5 | 50 | 0 | 0 | 100 | 55 |
| | Зеленоградский район | 4,3 | 100 | 33 | 0 | 67 | 44 |
| | Неманский МР | 4 | 100 | 0 | 0 | 100 | 52 |
| | Полесский ГО | 3 | 0 | 0 | 0 | 100 | 54 |
| | Светловский ГО | 4 | 100 | 0 | 100 | 0 | 68 |
| | Советский ГО | 4 | 100 | 0 | 0 | 100 | 58 |
| | Черняховский МР | 3,6 | 33 | 33,3 | 66,7 | 0 | 63 |
| | Регион | 2 | 0 | 0 | 0 | 100 | 18 |
| | В среднем | 3,39 | 50 | 11 | 17 | 72 | 50 |
