Магистерская диссертация

Вид материала

Диссертация

Содержание Вывод формулы.

Подобный материал:

• Название: Магистерская диссертация. Методика написания, правила оформления и процедура, 1519.29kb.
• Магистерская программа «Государственные и муниципальные финансы» Кафедра государственного, 867.91kb.
• Магистерская программа Прикладная экономика Кафедра магистерская диссертация роль лизинга, 822.73kb.
• Магистерская программа «Государственные и муниципальные финансы» Кафедра государственного, 470.54kb.
• Борис никольский (3/15 октября 1870, Санкт-Петербург — начало лета 1919, Петроград), 241.17kb.
• Магистерская диссертация, 1281.12kb.
• Магистерская диссертация, 1462.15kb.
• Правительстве Российской Федерации Высшая школа финансового менеджмента Магистерская, 1925.58kb.
• Новосибирский Государственный Университет Экономический факультет Кафедра теоретической, 1603.03kb.
• М. В. Ломоносова Экономический факультет Кафедра «Финансы и кредит» Магистерская диссертация, 895.77kb.

Приложения

В Приложении 1 приведено доказательство модели Пэддока, Сигела и Смита для нефтяного сектора.

В Приложениях 2 и 3 продемонстрированы результаты расчетов по инвестиционному проекту биномиальным методом для двух случаев: без заимствования и случая с привлечением сторонних инвесторов. Использован интерфейс программы DerivaGem для Microsoft Excel, разработанной Халлом [11].


Приложение 1. Вывод уравнения в частичных дифференциалах для модели Пэддока, Сигела и Смита

Условные обозначения:

• F : удельная стоимость неразработанного резерва ($/баррель). F (V, t);
  
• V : то же для разработанного резерва ($/баррель). Функция цены;
  
•  : прибыль (за вычетом налогов) от производства и продажи барреля нефти (функция времени);
  
• B : оставшийся запас нефти (баррели) (функция времени);
  
• : доля запаса (падает по экспоненте), добываемая за год;
  
• R : поступления собственнику запаса ($/год);
  
• D : издержки инвестирования в расчете на баррель нефти;
  
• r : реальная безрисковая процентная ставка;
  
• : волатильность разработанного резерва (стандартное отклонение величины dV/V) (% в год);
  
• : корректированная с учетом риска доходность от единицы разработанного резерва (% в год);
  
• : дивидендный доход на единицу разработанного резерва (% в год);
  
• dz : винеровский дифференциал (случайный дифференциал).
  

Вывод формулы.

Экспоненциально затухающий процесс, применяемый в отрасли в качестве оценки продуктивности месторождения:

dB = -Bdt (1)

Доходность разработанного резерва = доход от добычи (дивиденд) + оценка оставшегося запаса (доход от капитала):

Rdt = Bdt + d(BV) (2)

П
олный дифференциал:


Используя выражение (1):

d(BV) = BdV - VBdt

Подставляем в (2):

Rdt = Bdt + Bdv - VBdt (3)

Д

(4)
ля модели, в которой ставка доходности разработанного резерва подчиняется геометрическому броуновскому движению:


Подставим (3) в (4) и проведем преобразования:





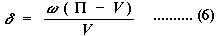
Дивидендный доход:

Лемма Ито для F (V, t ):





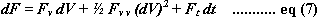
где нижние индексы обозначают частные производные.

Возводим в квадрат стохастическое уравнение (5); dt – бесконечно малая, можно игнорировать элементы где степень dt больше единицы:

(dV)² = ²V²dt (8)

dF = F_VdV + 1/2²V²F_VVdt + F_tdt (9)

Ценность безрискового портфеля:

Ф = F – nV = F - F_VV

Количество акций n, необходимое для безрискового портфеля, является производной опциона, поскольку обнуляет случайный элемент dz в уравнении доходности.

Портфельный доход в расчете на баррель:

RФdt = r(F – F_VV)dt (10)

Также его можно выразить как:

• Длинная позиция: dF (только доход от капитала);
  
• Короткая позиция (выражение (3), но в расчете на баррель):
  

F_V(dt + dV -Vdt)

Получим

dF - F_V(dt + dV -Vdt)

Приравняем к (10) и подставим dF в выражение (9):





Упростим (заметим, что элементы с dt исключаются):





Наконец, подставив дивидендный доход (6), получим уравнение в частичных дифференциалах по t и V:

1/2²V²F_VV + (r - )VF_V – rF = -F_t (11).

Приложение 2. Результаты подсчетов биномиальным методом в программе DerivaGem (без заимствования)

Underlying Data

Graph Results

Underlying Type:

Time

Dividend

Vertical Axis:

Horizontal Axis:

Stock Price:

623,00

Volatility (% per year):

9,00%

Risk-Free Rate (% per year):

4,00%

Minimum X value

498,4

Maximum X value

747,6

Option Data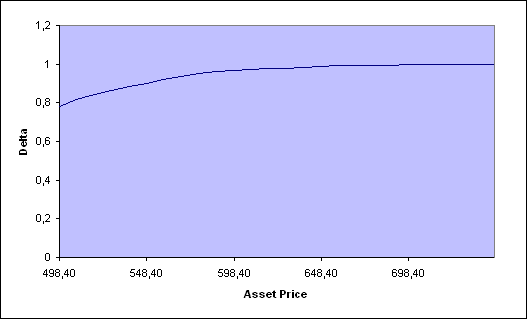

Option Type:

Time to Expiration:

3,9200

Exercise Price:

512,00

Tree Steps:

8

Price:

186,2042

Delta (per $):

0,977661

Gamma (per $ per $):

0,00055

Vega (per %):

0,707458

Theta (per day):

-0,04941

Rho (per %):

16,37827