Магистерская диссертация
| Вид материала | Диссертация |
- Название: Магистерская диссертация. Методика написания, правила оформления и процедура, 1519.29kb.
- Магистерская программа «Государственные и муниципальные финансы» Кафедра государственного, 867.91kb.
- Магистерская программа Прикладная экономика Кафедра магистерская диссертация роль лизинга, 822.73kb.
- Магистерская программа «Государственные и муниципальные финансы» Кафедра государственного, 470.54kb.
- Борис никольский (3/15 октября 1870, Санкт-Петербург — начало лета 1919, Петроград), 241.17kb.
- Магистерская диссертация, 1281.12kb.
- Магистерская диссертация, 1462.15kb.
- Правительстве Российской Федерации Высшая школа финансового менеджмента Магистерская, 1925.58kb.
- Новосибирский Государственный Университет Экономический факультет Кафедра теоретической, 1603.03kb.
- М. В. Ломоносова Экономический факультет Кафедра «Финансы и кредит» Магистерская диссертация, 895.77kb.
§ 2.3 Основные характеристики модели Блэка-Шоулза и биномиальной модели.
Приведем вкратце основные концепции моделей, которые будут использованы автором при проведении расчетов.
Для математических моделей ценообразования опционов существует ряд основных положений.
- Изменение цены актива – случайный процесс, в теории характеризующийся логнормальным (логарифмически нормальным) распределением. Это связано с тем, что кривая такого распределения не имеет отрицательных значений и указывает на большую вероятность увеличения случайной величины, нежели ее падения (что лучше соответствует поведению цен, чем нормальное распределение) [2].
П
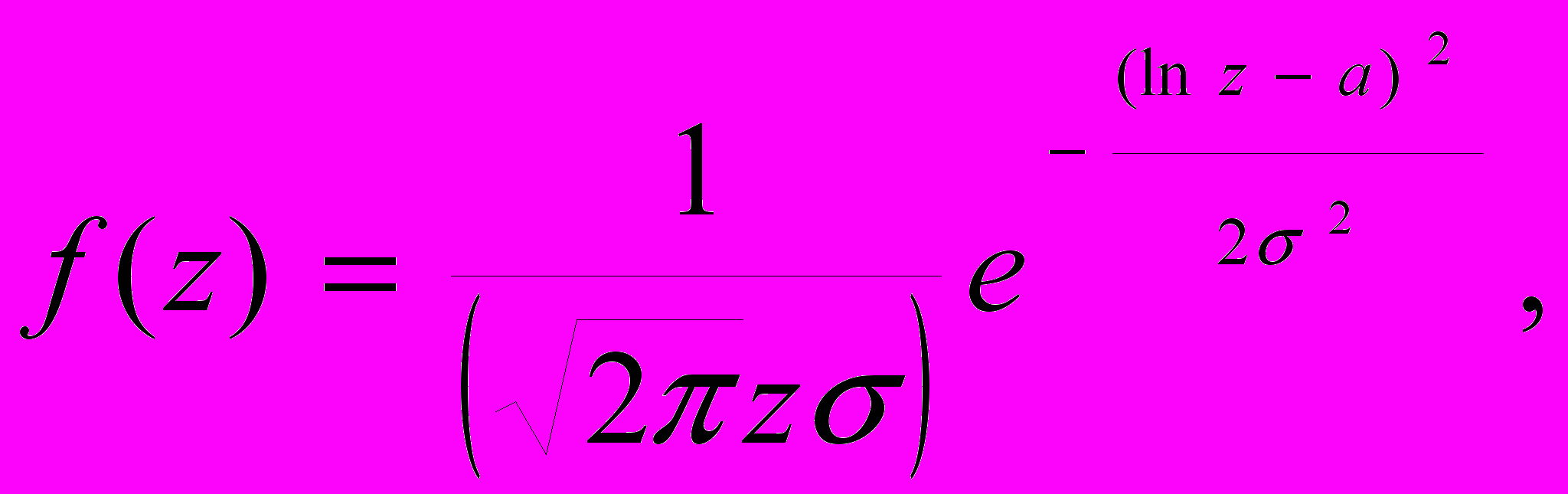
лотность логнормально распределенной случайной величины z = ex записывается следующим образом:
где a – мат. ожидание нормально распределенной величины x, а 2 – ее дисперсия.
- Е
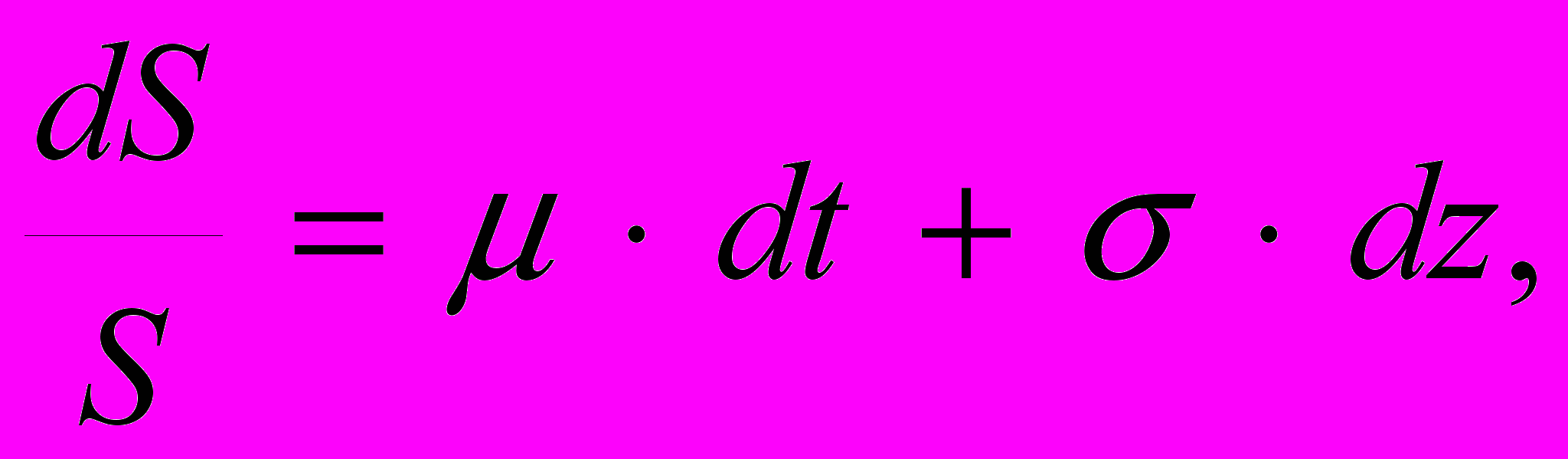
сли S(t) - спот-цена актива в момент t, то изменение цены описывается стохастическим процессом Ито, выражающимся уравнением
где z – винеровский процесс, - ожидаемая доходность актива, - отклонение цены от ожидаемого изменения.
В
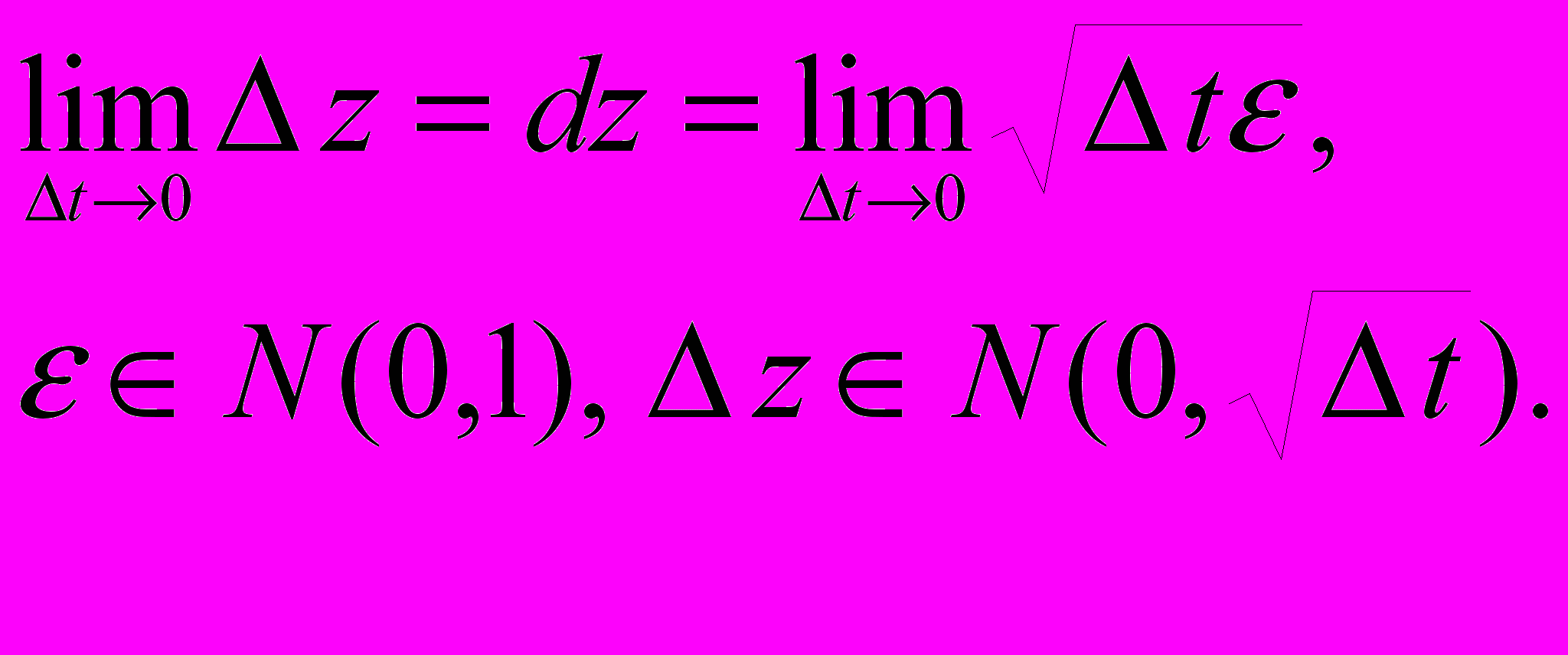
инеровский случайный процесс - процесс X(t), 0
- В моделях рассматривается непрерывное начисление процента.
- Выполняются гипотезы Блэка – Шоулза: эффективность рынка, отсутствие возможности арбитража, нулевые трансакционные издержки.
В начале 1970-х гг. Блэк и Шоулз создали модель оценки премии европейских опционов (впервые опубликованную в статье F. Black, and M. Scholes, “The Pricing of Options and Corporate Liabilities”, Journal of Economics (May 1973)).
Выплаты в день истечения европейского колл-опциона равны
max (ST-X, 0).
Текущая цена европейского колл-опциона равна
c = e-r(T-t)E(max (ST-X, 0)),
где Е(x) – ожидание величины x:
E(x) =
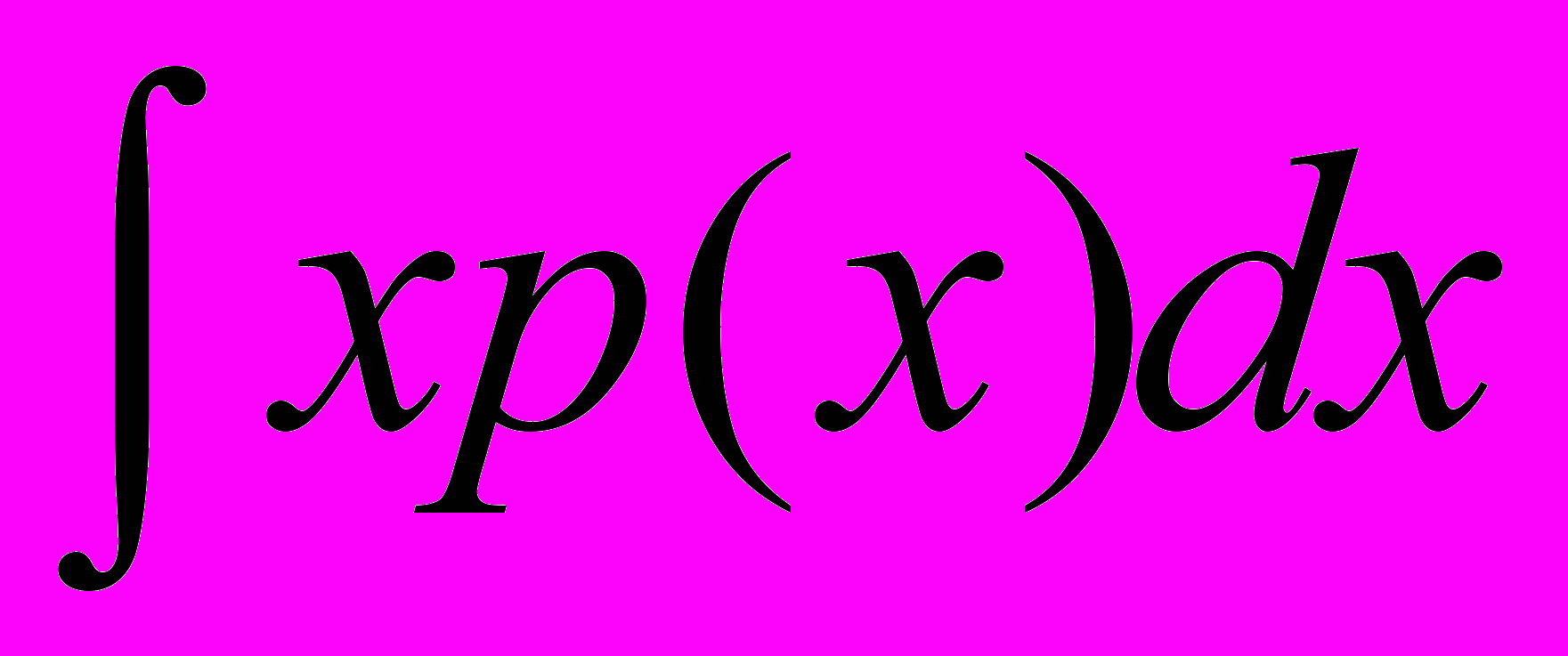,p(x) – вероятность достижения величиной x этого значения.
Предположим, что цена базового актива распределена логнормально:
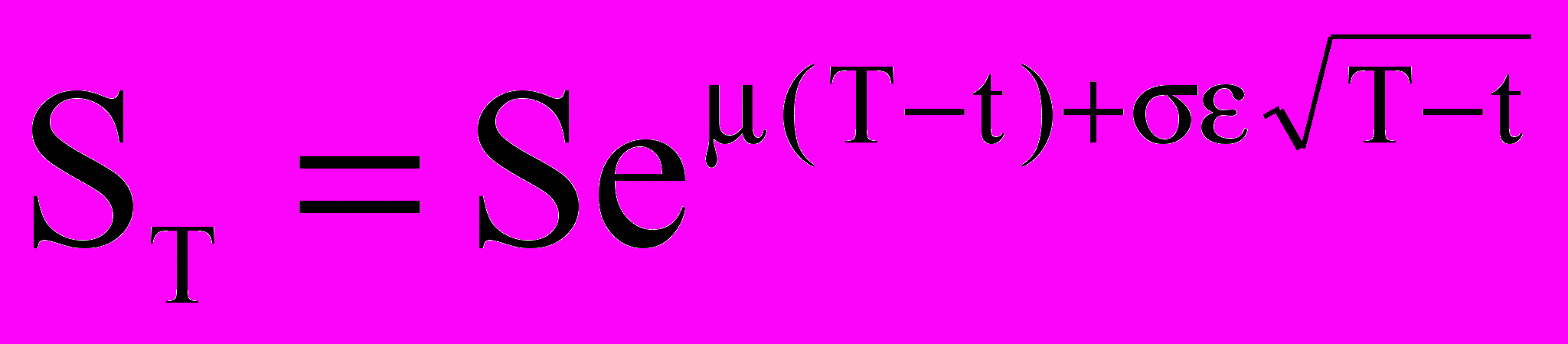, где μ = r – σ2/2. Следовательно,
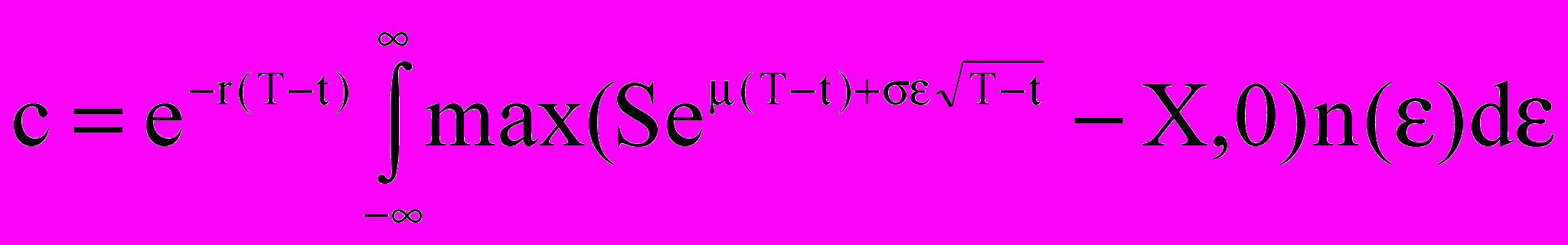, где n(x) =
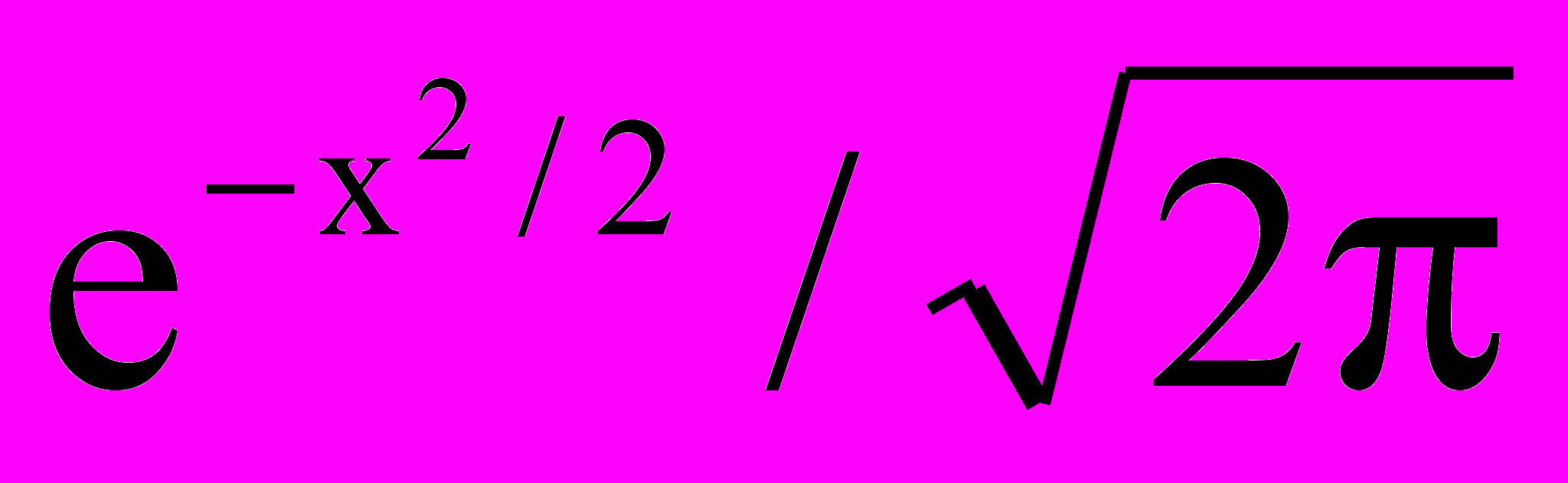- функция нормального распределения. Поскольку подынтегральное выражение обращается в ноль при значениях ε, меньших величины
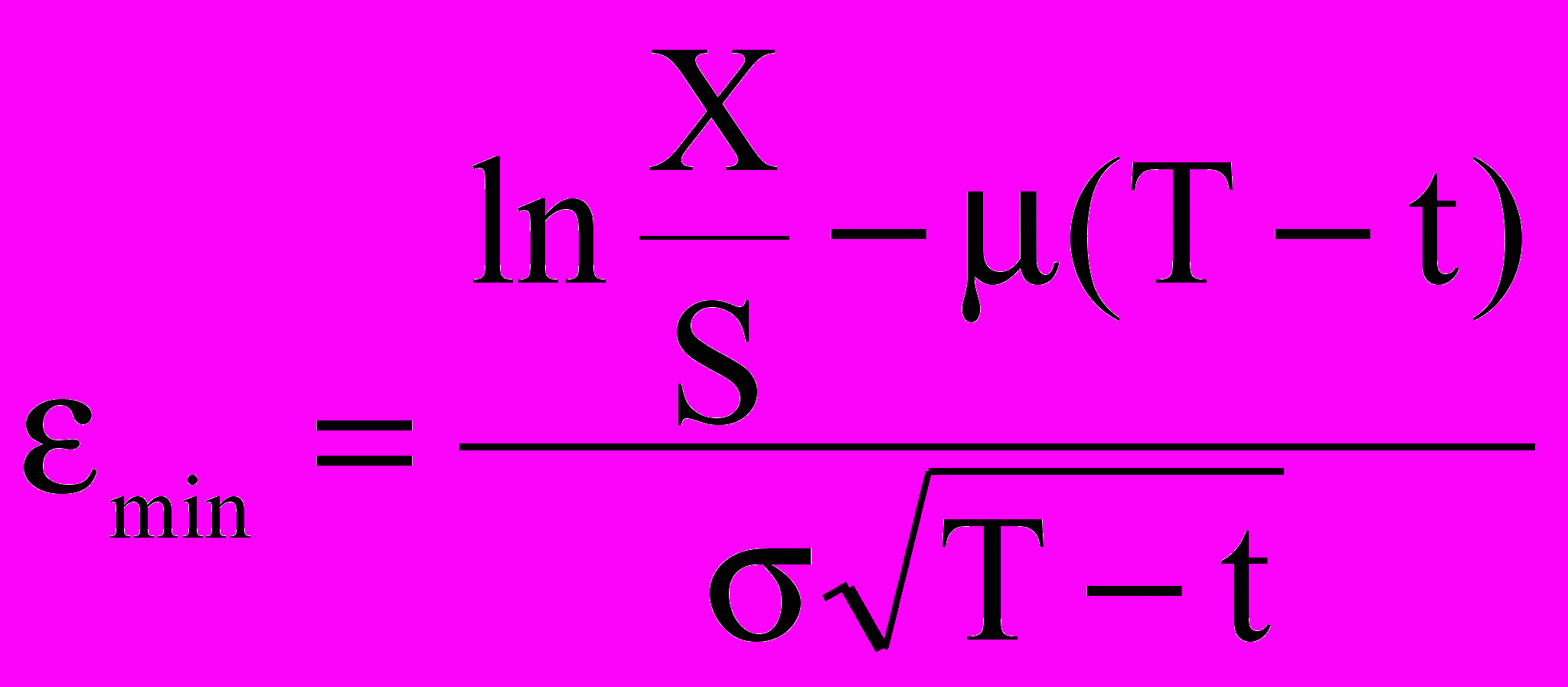,то
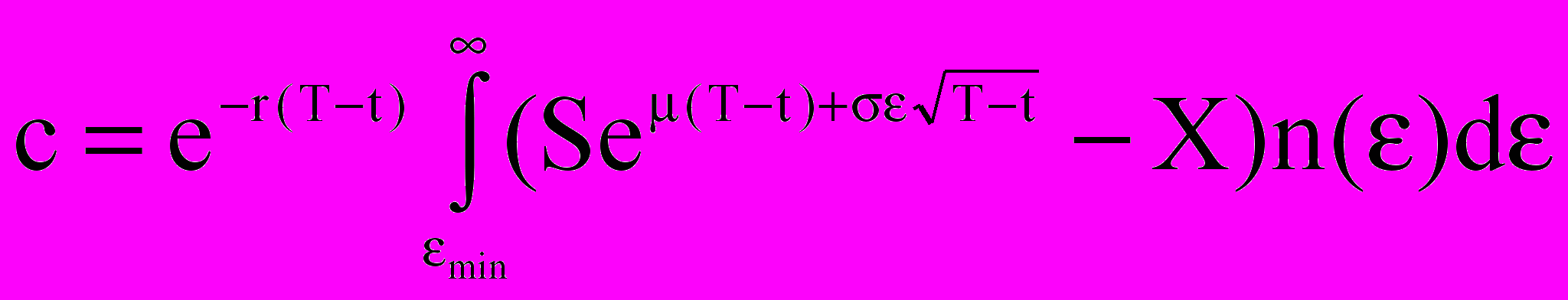.Вычисления интегралов позволяют получить формулу Блэка-Шоулза:
c = SN(d1) – e-r(T-t)XN(d2),
где
N(x) =
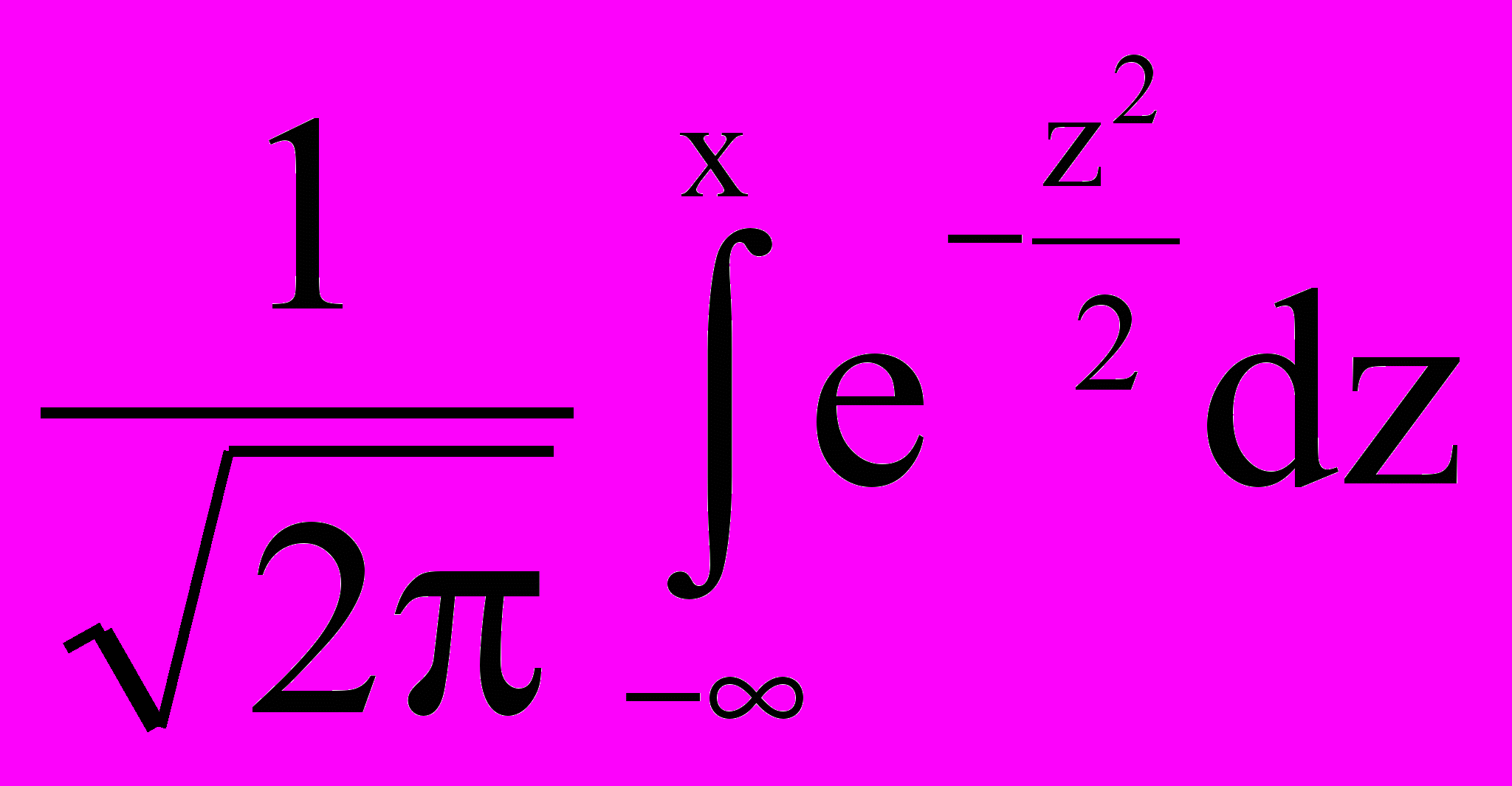- функция стандартного нормального распределения, d1 =
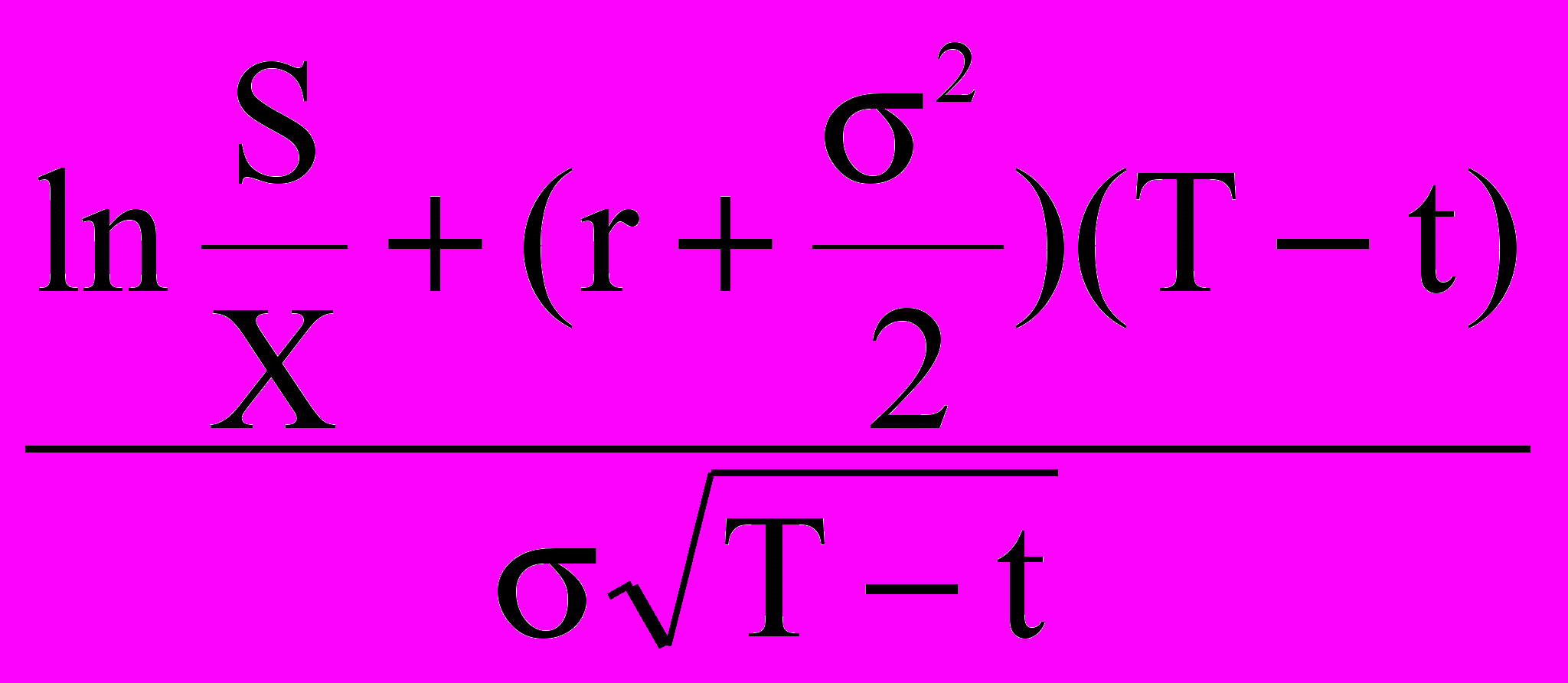, d2 = 
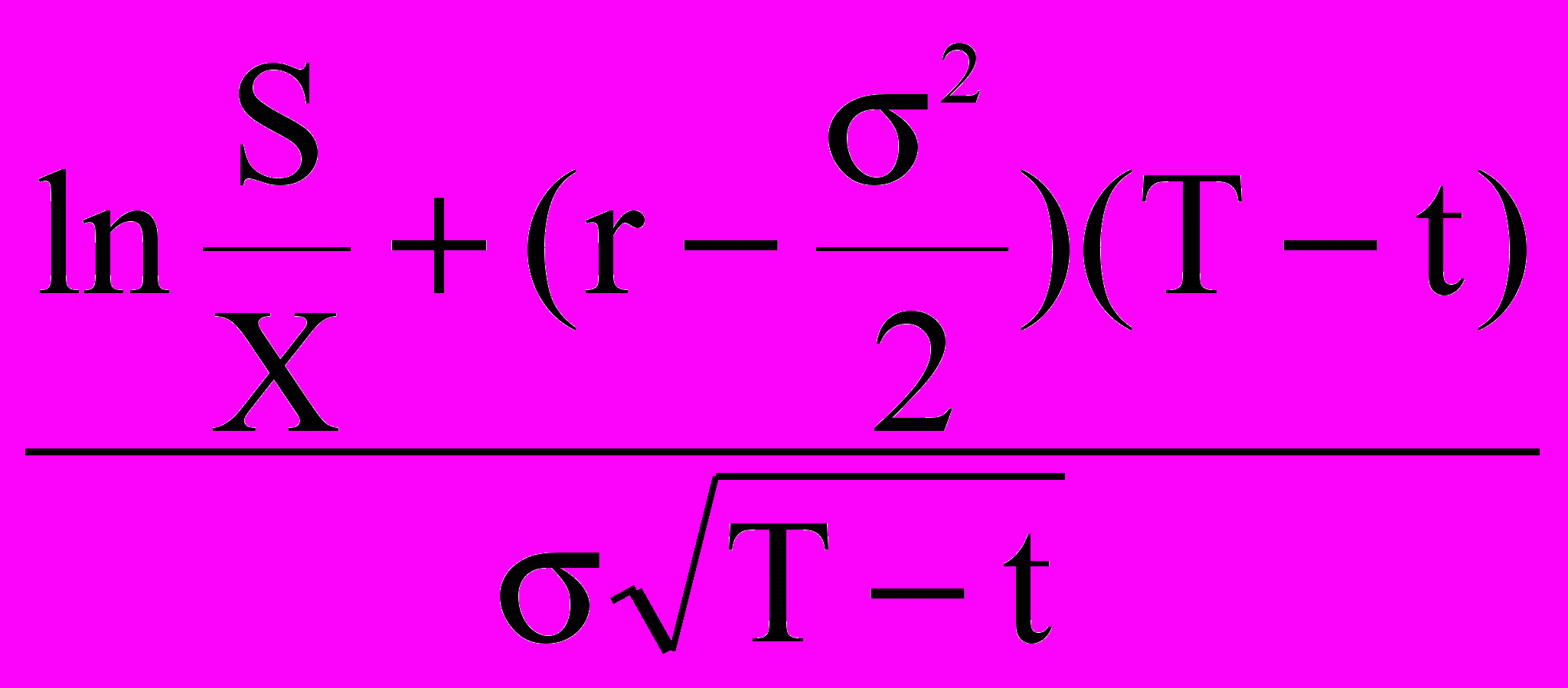.Текущая цена европейского пут-опциона равна
p = e-r(T-t)E(max(X-ST, 0).
Проводя аналогичные вычисления, получаем формулу
p = e-r(T-t)XN(-d2) – SN(-d1).
(разумеется, последнюю формулу можно получить и с помощью пут-колл паритета) [2].
Биномиальные модели предполагают, что основная случайная переменная характеризуется биномиальным распределением. Применение биномиальных моделей к ценообразованию опционов подразумевает моделирование цены актива, лежащего в основе опциона как биномиального процесса, будь то цена ценной бумаги, обменный курс или процентная ставка, для определения распределения этой переменной на момент исполнения. Затем с использованием ограничивающих условий определяется будущая стоимость опциона и дисконтируется к настоящей, определяя таким образом текущую цену на опцион.
Биномиальная модель допускает возможность создания безрискового портфеля посредством хеджирования длинной позиции по активу короткой позицией по ряду справедливо оцененных опционов по покупке этого актива. Следовательно, только безрисковая процентная ставка должна быть использована для дисконтирования, поскольку предполагается, что если портфель захеджирован наилучшим образом, он будет безрисковым и, следовательно, должен характеризоваться безрисковой процентной ставкой.
Основные подходы – это построение биномиальной решетки (или дерева), а также использование биномиальной алгебры для получения суммы текущих стоимостей каждой вероятностно взвешенной будущей стоимости опциона.
Построение решетки проходит просто. В каждом конкретном периоде цена может расти либо падать, u – коэффициент движения вверх цены актива (1 + относительный прирост цены), а d – коэффициент движения вниз цены актива (1 - относительное падение цены). Необходимо также условие d < (1+r) < u, поскольку если d и u меньше, чем безрисковая ставка, безрисковый актив всегда будет иметь более высокие доходы, чем рисковый актив, что вступает, конечно же, в противоречие с финансовой теорией.
Биномиальный подход может быть обобщен таким образом, что срок действия опциона может быть разделен на любое количество временных периодов или биномиальных испыытаний. В самом деле, если временной интервал между периодами становится бесконечно малым, то есть торговля происходит непрерывно, биномиальная модель становится моделью Блэка-Шоулза.
Величины u и d, которые относятся к волатильности актива, должны быть определены на основе рыночной информации и скорректированы в соответствии с количеством биномиальных испытаний. Кокс в 1979 году показал, что u и d соотносятся со средним квадратическим отклонением следующим образом:
u =
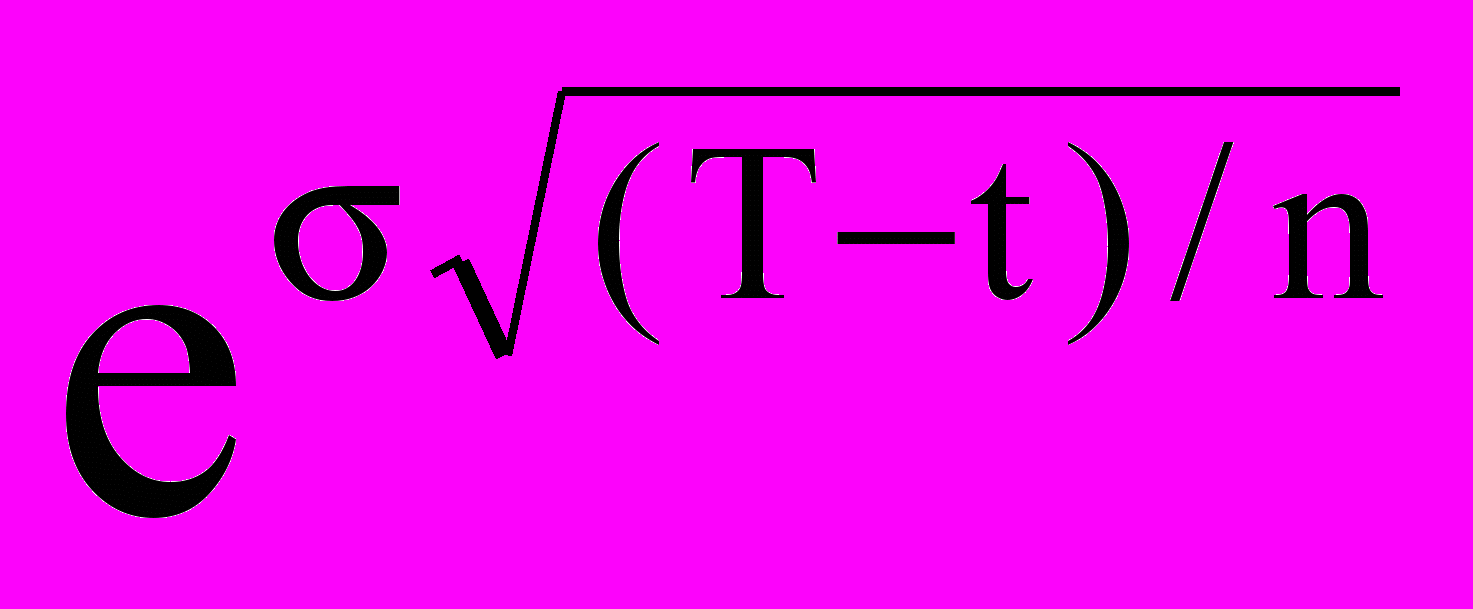, d =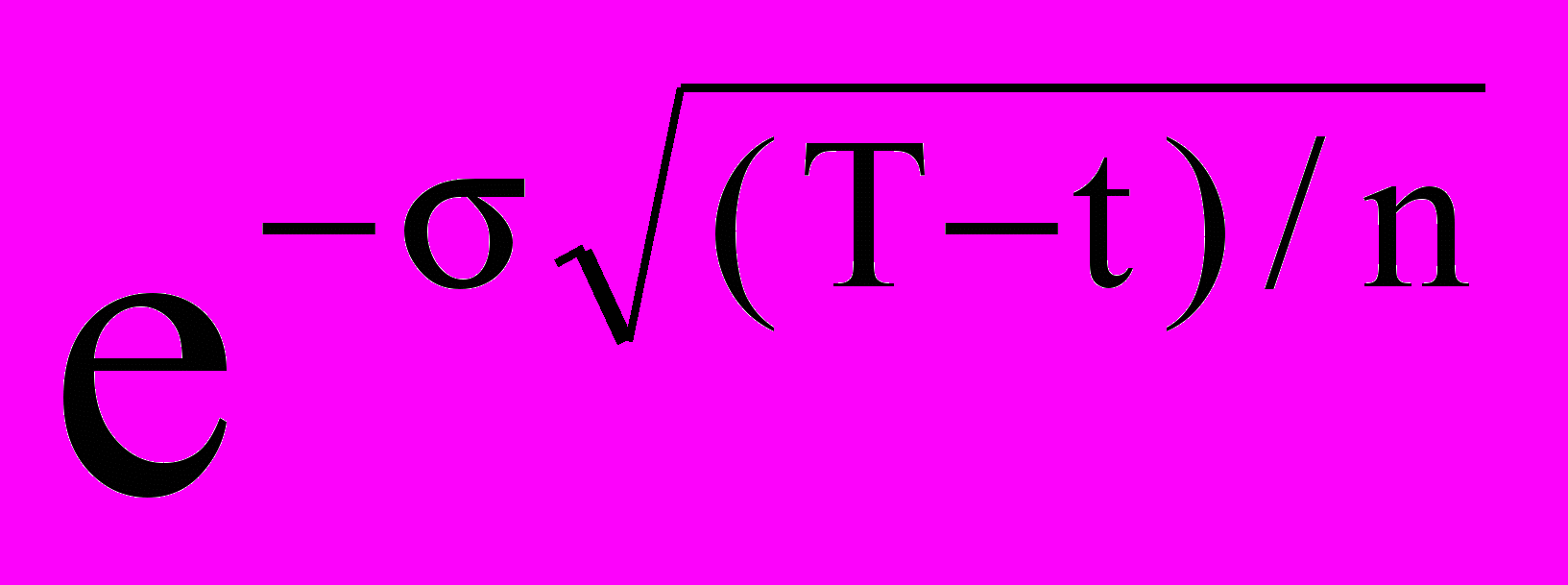 
,где (T-t) – срок действия опциона в годах или долях лет, а n – количество биномиальных испытаний.
Обычно также требуется, чтобы u = 1/d, благодаря чему движение цены вверх с последующим движением вниз равнозначно движению вниз с последующим движением вверх. В этом случае видоизмененное биномиальное дерево называется биномиальной решеткой. Следовательно, движение вверх и вниз определяется изменчивостью переменной, средним квадратическим отклонением натурального логарифма отношений цен активов, т.е. средним квадратическим отклонением непрерывно наращенного дохода.
С помощью решетки мы можем рассчитать различные стоимости основного актива к финальному периоду, а также потенциально возможные стоимости опциона на момент исполнения. Далее находятся потенциальные стоимости опциона на предыдущий период, и так до начального момента, что и дает нам премию опциона. В главе 3 автором будет продемонстрирована конкретная биномиальная решетка для подсчетов по проекту.
Приведем также общую биномиальную формулу для оценки опциона.
Для опциона на покупку:
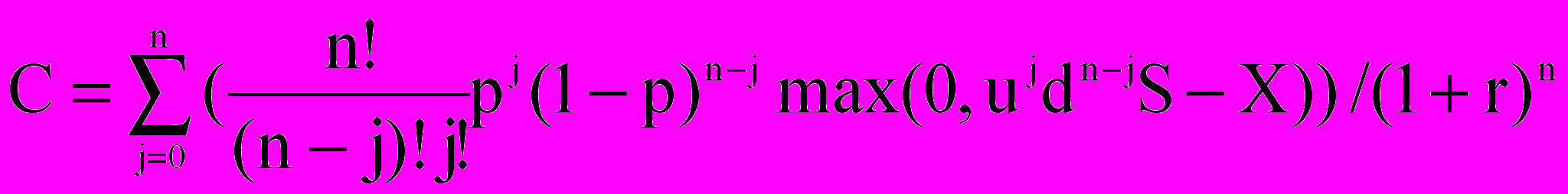.Для опциона на продажу:
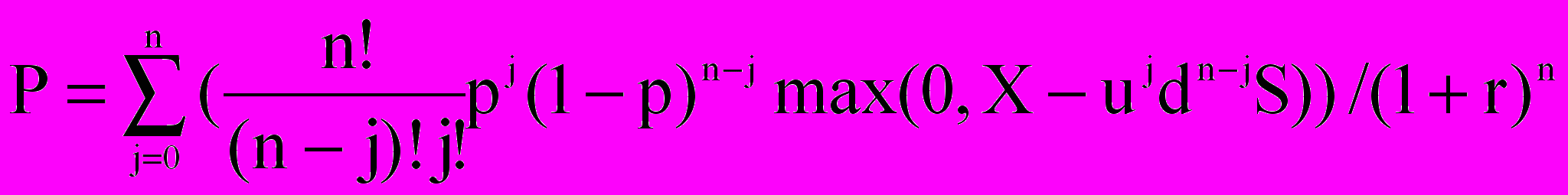,где j – количество произошедших движений вверх, а n-j – количество произошедших движений вниз [2].
Теперь, когда выполнены все предпосылки к проведению расчетов, можно приступать к рассмотрению конкретного инвестиционного проекта и выполнению необходимых аналитических выкладок. Это станет предметом рассмотрения в третьей главе.