Методика экспертизы программ основных и специальных курсов 6 Аналитическая справка 15
| Вид материала | Бюллетень |
СодержаниеФормулы для оценки заданий с несколькими правильными ответами Формула (1) Эталон ответа Формула (2) Формула (2') Формула (3) Формула (4) Зарипов В.Н. |
- Алгоритм разработки программы учебного курса, 651.27kb.
- Учебно-тематический план программы курсов повышения квалификации «Модернизация систем, 22.98kb.
- Предоставление информации о реализации в образовательных муниципальных учреждениях, 6.85kb.
- Информационно-аналитическая справка по результатам деятельности муниципальной межшкольной, 622.44kb.
- Обзор специальных инструментальных средств и оболочек для создания курсов, 322.86kb.
- Судебно-экономические экспертизы по делам о криминальном банкротстве м. Г. Порохов,, 102.54kb.
- Ипкро ра рмк управления по образованию, спорту и молодежной политике мо «Усть-Канский, 177.48kb.
- Аналитическая справка Тузовой, 16.79kb.
- Методические рекомендации по проведению внутренней экспертизы деятельности университета, 1788.52kb.
- Методика расчёта трудоёмкости основных образовательных программ высшего профессионального, 13.8kb.
Формулы для оценки заданий с несколькими правильными ответами
При составлении теста чаще всего используются задания с выбором ответа. Если среди предлагаемых для выбора вариантов ответов правильным является только один, то оценивать задание очень легко: балл за выполнение такого задания равен 1, если задание выполнено верно, или 0, если задание выполнено неверно. В данной статье предлагаются формулы для оценки заданий с выбором правильного ответа в случае, когда таковых может быть несколько.
Пусть в задании с множественным выбором предлагается l вариантов для выбора, причем среди них имеется c правильных ответов. Пусть испытуемый при ответе сделал a правильных выборов и b неправильных. Как в этом случае выставить балл за выполнение этого задания?
Формула (1):
Очевидно, вес правильного ответа равен 1/c. Назначим для испытуемого, допустившего ошибки, "коэффициент наказания" (на который будем умножать вес ответа) в размере
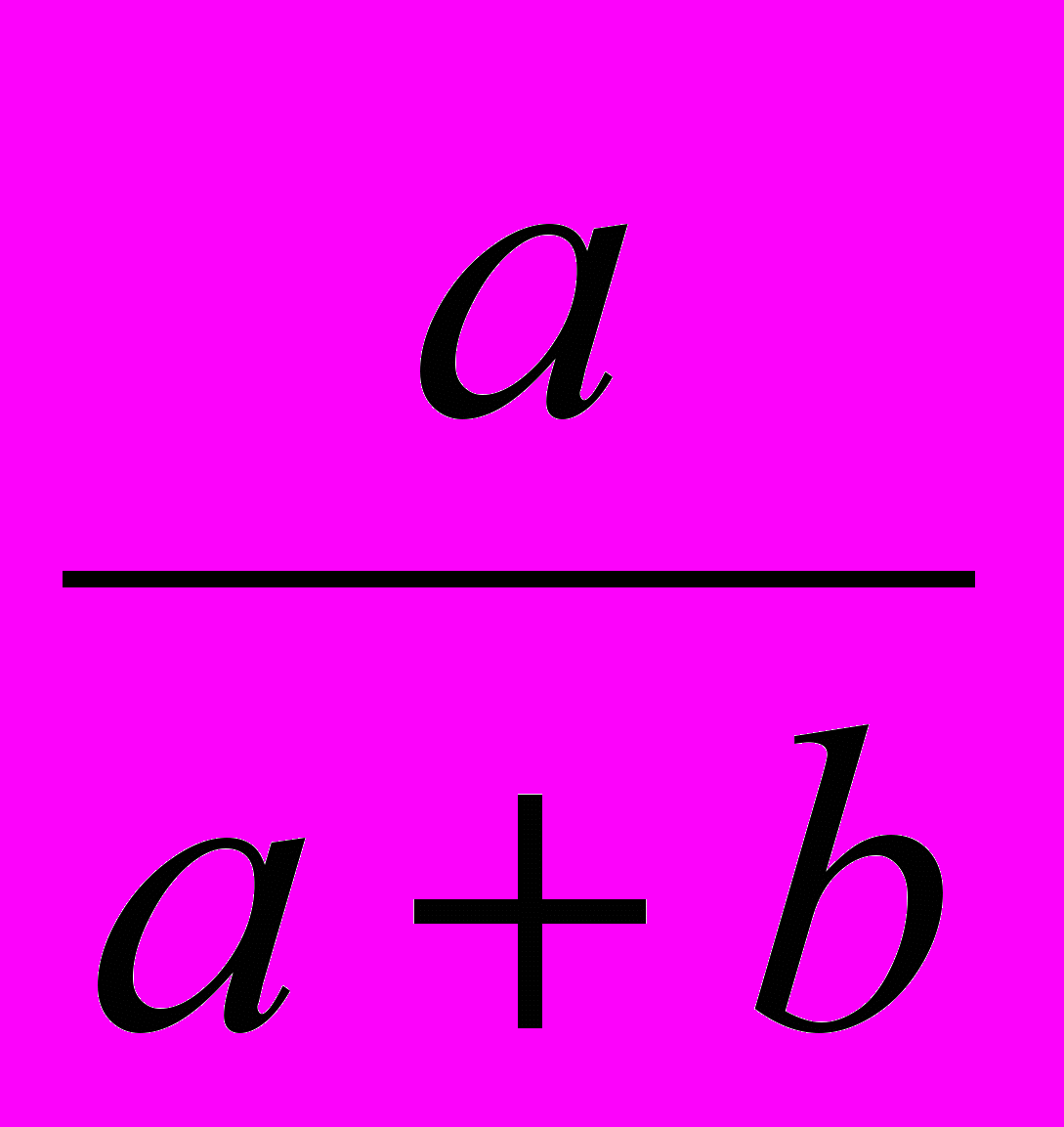 . Эта дробь представляет собой относительный вес правильных ответов в ответе испытуемого. Если испытуемый не допустил ни одной ошибки, то этот коэффициент равен единице и не меняет веса правильного ответа. В противном случае значимость правильного ответа снижается. Таким образом, окончательный вес правильного ответа равен
. Эта дробь представляет собой относительный вес правильных ответов в ответе испытуемого. Если испытуемый не допустил ни одной ошибки, то этот коэффициент равен единице и не меняет веса правильного ответа. В противном случае значимость правильного ответа снижается. Таким образом, окончательный вес правильного ответа равен 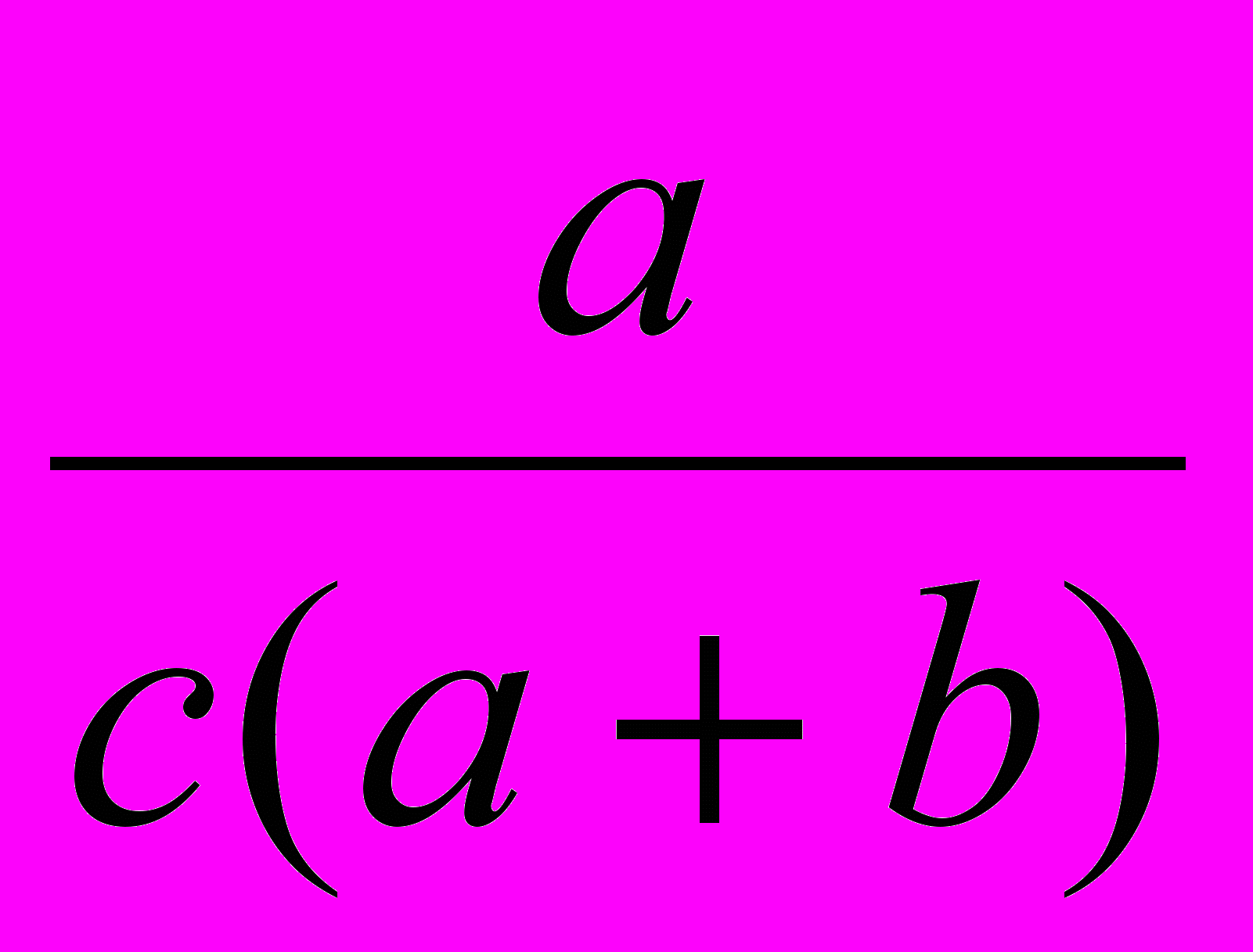 . Умножая вес правильного ответа на количество правильных ответов, получаем формулу:
. Умножая вес правильного ответа на количество правильных ответов, получаем формулу: 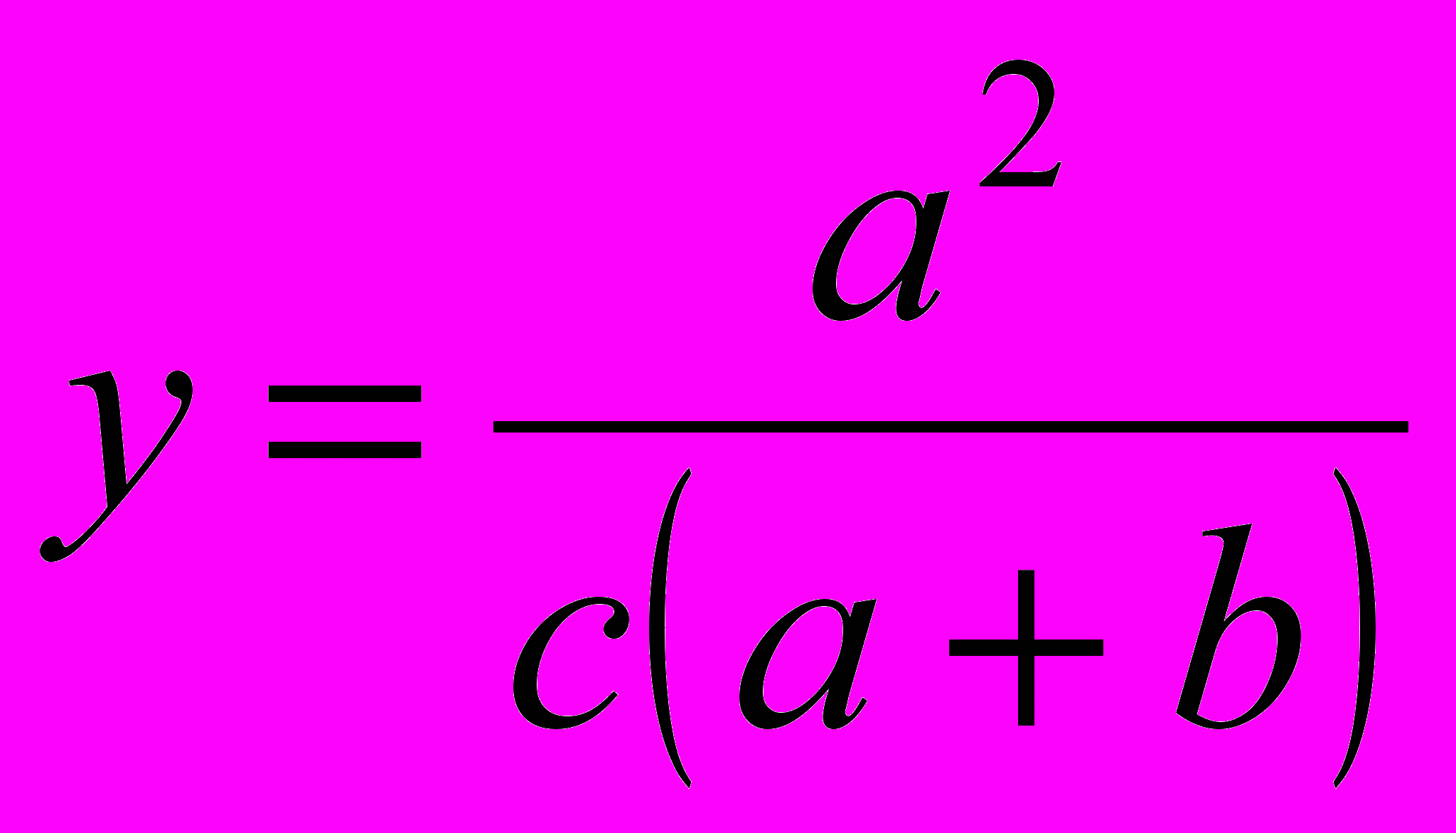 .
. Максимальный балл – единица – получается в случае, когда все выбранные варианты правильные (нет ни одного неправильного ответа). Минимальное значение, равное нулю, получается в случае, когда испытуемый не дал ни одного правильного ответа (при любом количестве неправильных ответов).
Эта формула обладает двумя недостатками. Первый заключается в проблеме нулевого знаменателя в случае, когда задание испытуемым пропущено (разумеется, в этом случае можно назначать ноль баллов, но это не будет результатом применения формулы). Второй недостаток – отсутствие дифференцирующего эффекта. Заметим, что ноль по этой формуле получается при отсутствии правильных ответов и любом количестве неправильных выборов. Тем самым одинаковый балл назначается испытуемому, пропустившему задание (возможно, ему просто не хватило времени), и всем испытуемым, не давшим верного ответа (хотя в каком-то смысле испытуемый, сделавший два неверных выбора, хуже испытуемого, допустившего лишь одну ошибку). Можно показать, что одинаковый балл возможен и в других ситуациях. Пусть, например, первый испытуемый дал a1 правильных ответов (но не все), а второй испытуемый дал a2 правильных (a2 > a1) и b неправильных ответов. Если
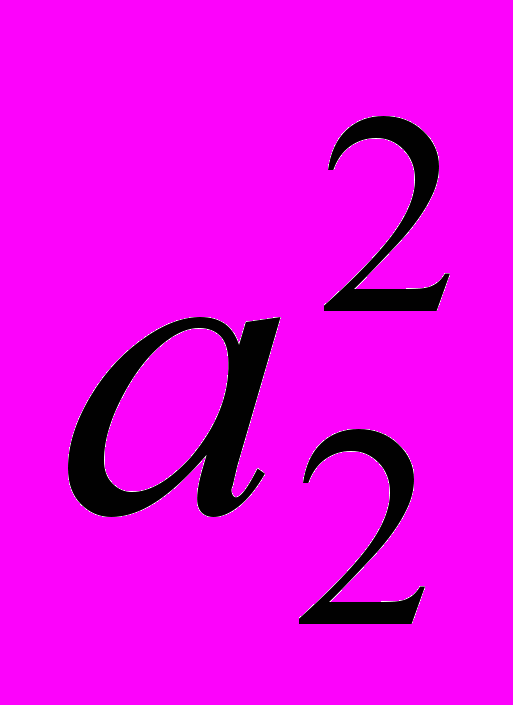 делится нацело на a1, то балл у испытуемых будет одинаков при количестве ошибок
делится нацело на a1, то балл у испытуемых будет одинаков при количестве ошибок 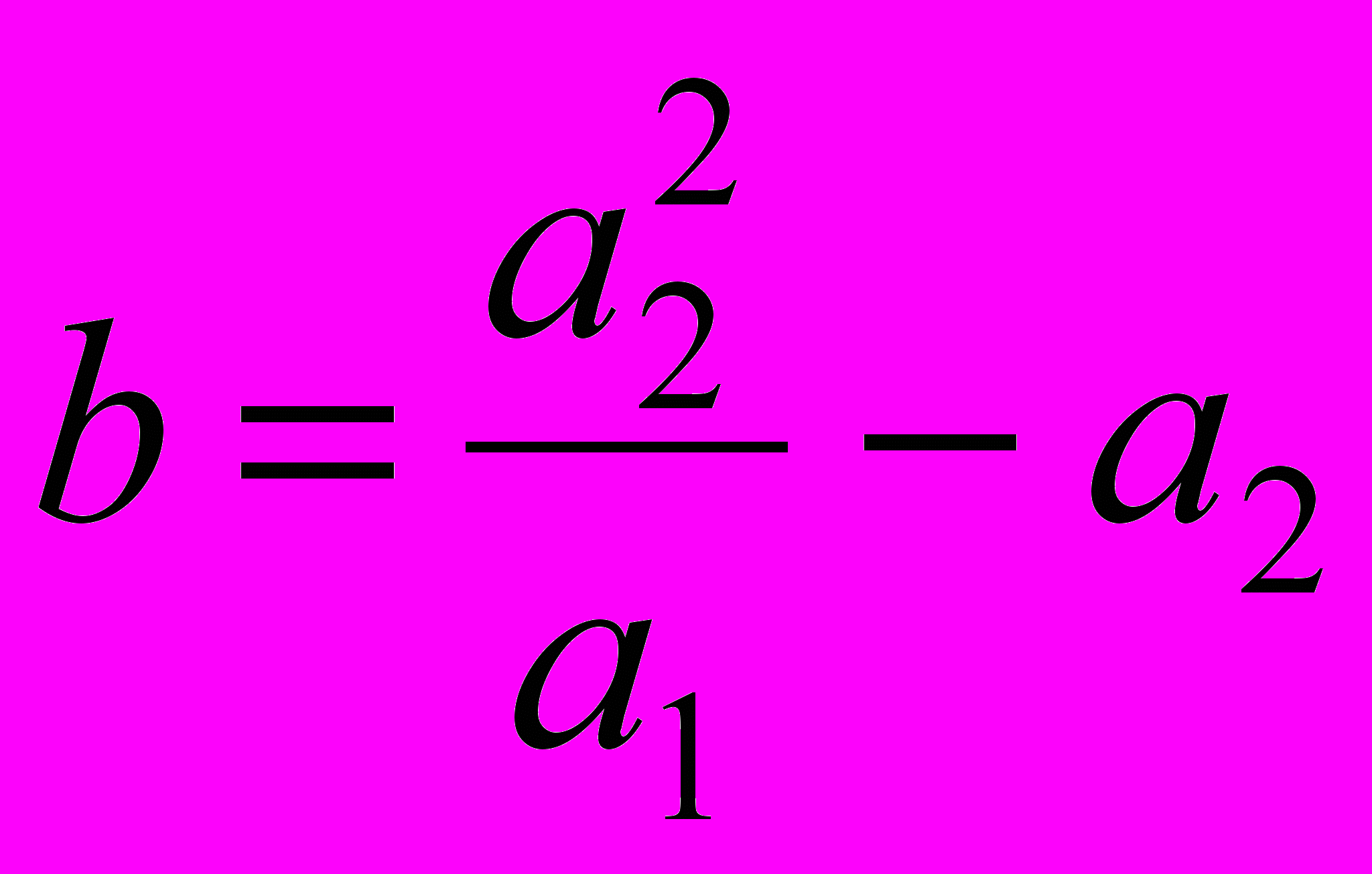 . В примере, приведенном ниже, именно такая ситуация складывается для третьего и десятого испытуемого. Все это позволяет рекомендовать использование данной формулы при критериально-ориентированном подходе, но не в нормативно-ориентированном тесте.
. В примере, приведенном ниже, именно такая ситуация складывается для третьего и десятого испытуемого. Все это позволяет рекомендовать использование данной формулы при критериально-ориентированном подходе, но не в нормативно-ориентированном тесте.Пример.
Пусть в задании с пятью вариантами для выбора три являются правильными. Рассмотрим все возможные варианты ответов испытуемых (см. табл. 1). В последнем столбце таблицы содержится результат расчетов по формуле (1). Ноль для четвертого испытуемого помечен звездочкой для того, чтобы подчеркнуть, что это результат договоренности, а не применения формулы.
Таблица 1
| № испыт | Эталон ответа | a | b | y | ||||
| х | х | х | | | ||||
| 1 | х | х | х | | | 3 | 0 | 1 |
| 2 | х | х | | | | 2 | 0 | 0,67 |
| 3 | х | | | | | 1 | 0 | 0,33 |
| 4 | | | | | | 0 | 0 | 0* |
| 5 | х | х | х | | х | 3 | 1 | 0,75 |
| 6 | х | х | | | х | 2 | 1 | 0,44 |
| 7 | х | | | | х | 1 | 1 | 0,17 |
| 8 | | | | | х | 0 | 1 | 0 |
| 9 | х | х | х | х | х | 3 | 2 | 0,6 |
| 10 | х | х | | х | х | 2 | 2 | 0,33 |
| 11 | х | | | х | х | 1 | 2 | 0,11 |
| 12 | | | | х | х | 0 | 2 | 0 |
Во-первых, этот пример позволяет продемонстрировать отсутствие дифференциации испытуемых, не давших ни одного правильного ответа. Также заметим, что третий (один правильный ответ) и десятый (два правильных и два неправильных ответа) испытуемые получили одинаковый балл.
Во-вторых, покажем, что вклад правильного (так же, как и неправильного) ответа для различных испытуемых получается неодинаковым. Очевидно, для испытуемых, не допустивших ошибок, вес правильного ответа равен 1/3. Сравнивая ответ пятого и первого испытуемого, получаем, что разница в баллах составляет 0,25, а поскольку различие в ответах состоит только в одной ошибке пятого испытуемого, то один неправильный ответ пятого испытуемого понижает балл на 0,25 (вклад ошибки), и каждый правильный ответ тогда вносит в оценку 0,75:3=0,25. Сравнивая второго и шестого, получаем, что вклад ошибки для шестого равен 0,33, а вклад правильного ответа 0,055. Если же сравнивать пятого испытуемого с шестым, то получится вклад правильного ответа для пятого испытуемого равен 0,75-0,44=0,31. Таким образом, по формуле (1) мы можем соотнести балл испытуемого с абсолютным нулем или единицей, но не можем сравнить испытуемых друг с другом.
Формула (2):
Оценку за задание будем рассчитывать следующим образом: добавляем некоторую величину за каждый правильный ответ, вычитаем некоторую величину за каждый неправильный ответ и добавляем некоторую величину за "недопущенную ошибку". Обозначим вес правильного ответа wa, неправильного – wb, вес "недопущенной ошибки" – wn. Оценка испытуемого в этом случае будет равна
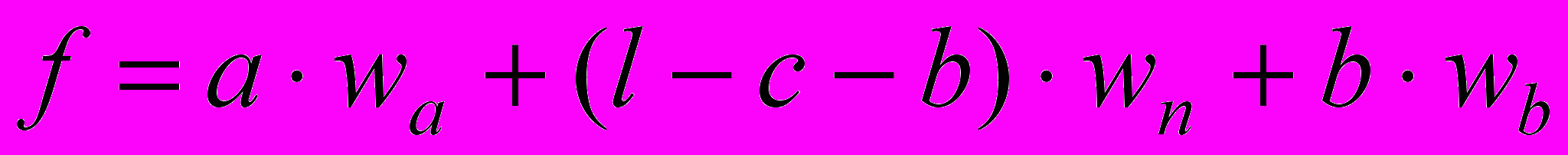 .
.Для расчета весов используем следующие соображения. Если даны все правильные ответы и не допущено ни одной ошибки, ставим 1. Если даны все ответы (и правильные и неправильные), то за такой ответ ставим 0 (испытуемый это задание не решал). Если не дано ни одного ответа (ни правильного, ни неправильного), то это означает, что испытуемый пропустил задание; считаем, что это лучше, чем если бы он начал отвечать неправильно или угадывать правильный ответ. Поэтому за ответ "пусто" назначаем балл чуть выше (разницу – насколько выше – обозначим через t), чем за ответ, содержащий все правильные варианты, но с ошибкой.
Тогда имеем следующие соотношения:
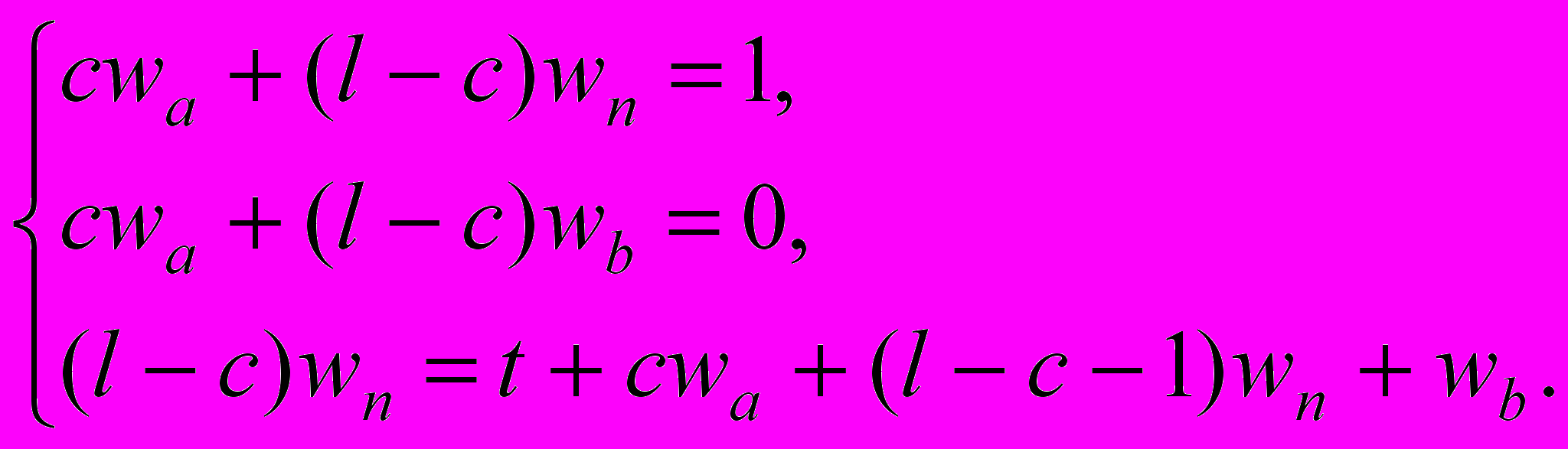
Решаем эту систему, считая t свободным параметром. Тогда получаем:
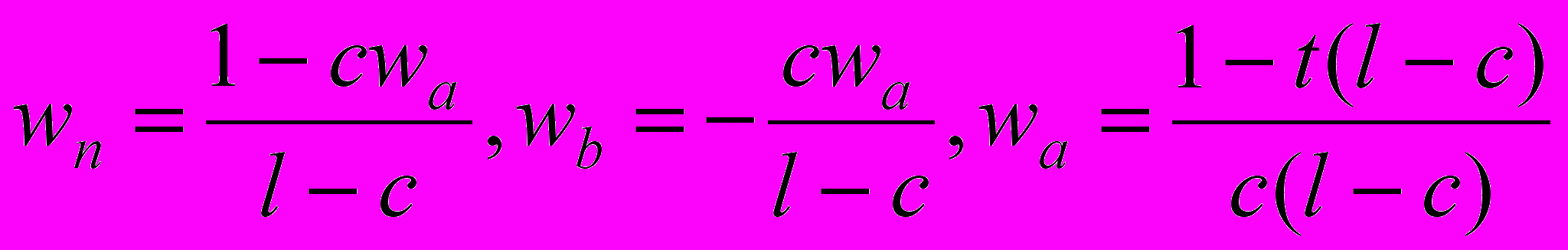 .
.Поскольку число правильных не равно общему количеству предложенных вариантов, то все формулы корректно определены.
Максимум (как было отмечено выше) равен fmax = 1. Минимум
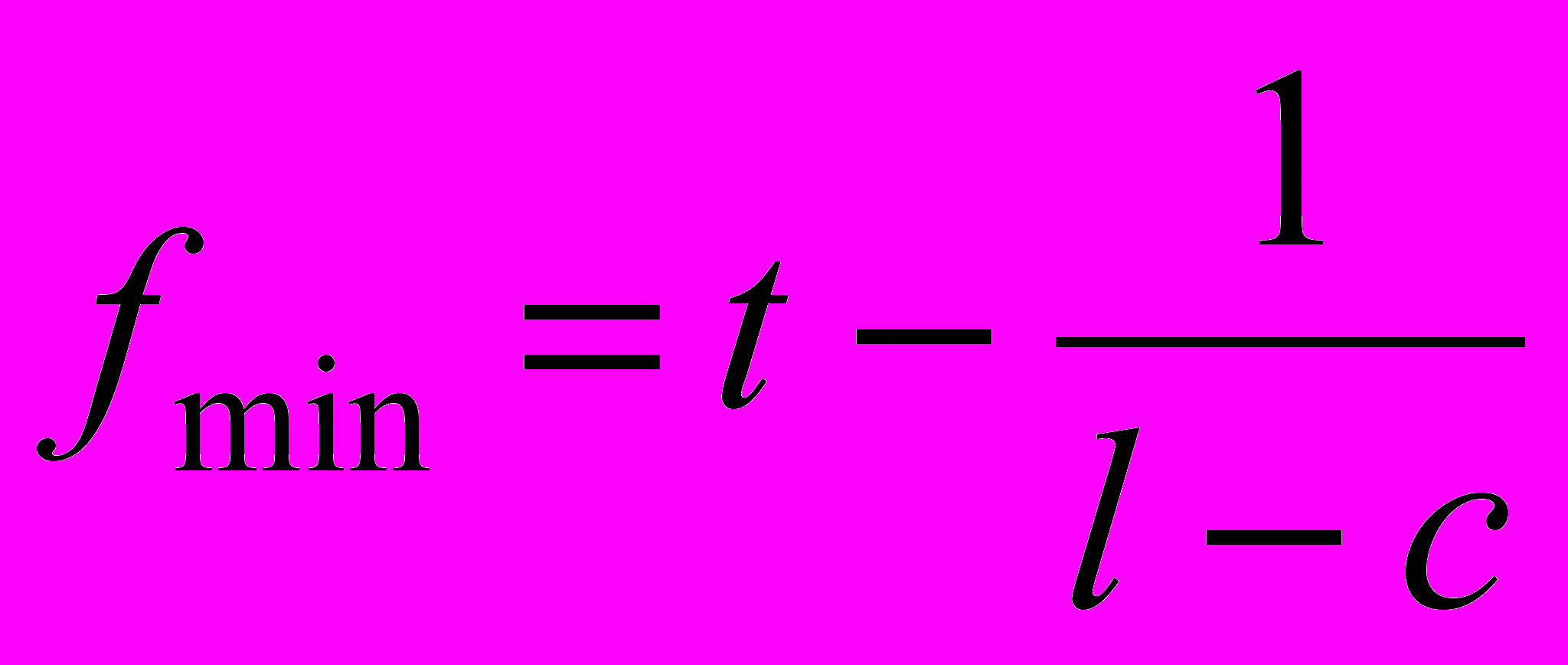 получается в ситуации, когда не дано ни одного правильного ответа, но выбраны все неправильные варианты.
получается в ситуации, когда не дано ни одного правильного ответа, но выбраны все неправильные варианты.Вообще говоря, величину t можно выбирать произвольно. Заметим, что если выбрать сразу t таким, чтобы fmin = 0, то wa = wb = 0, что нарушает дифференцирующий эффект формулы. Поэтому рекомендуется выбирать
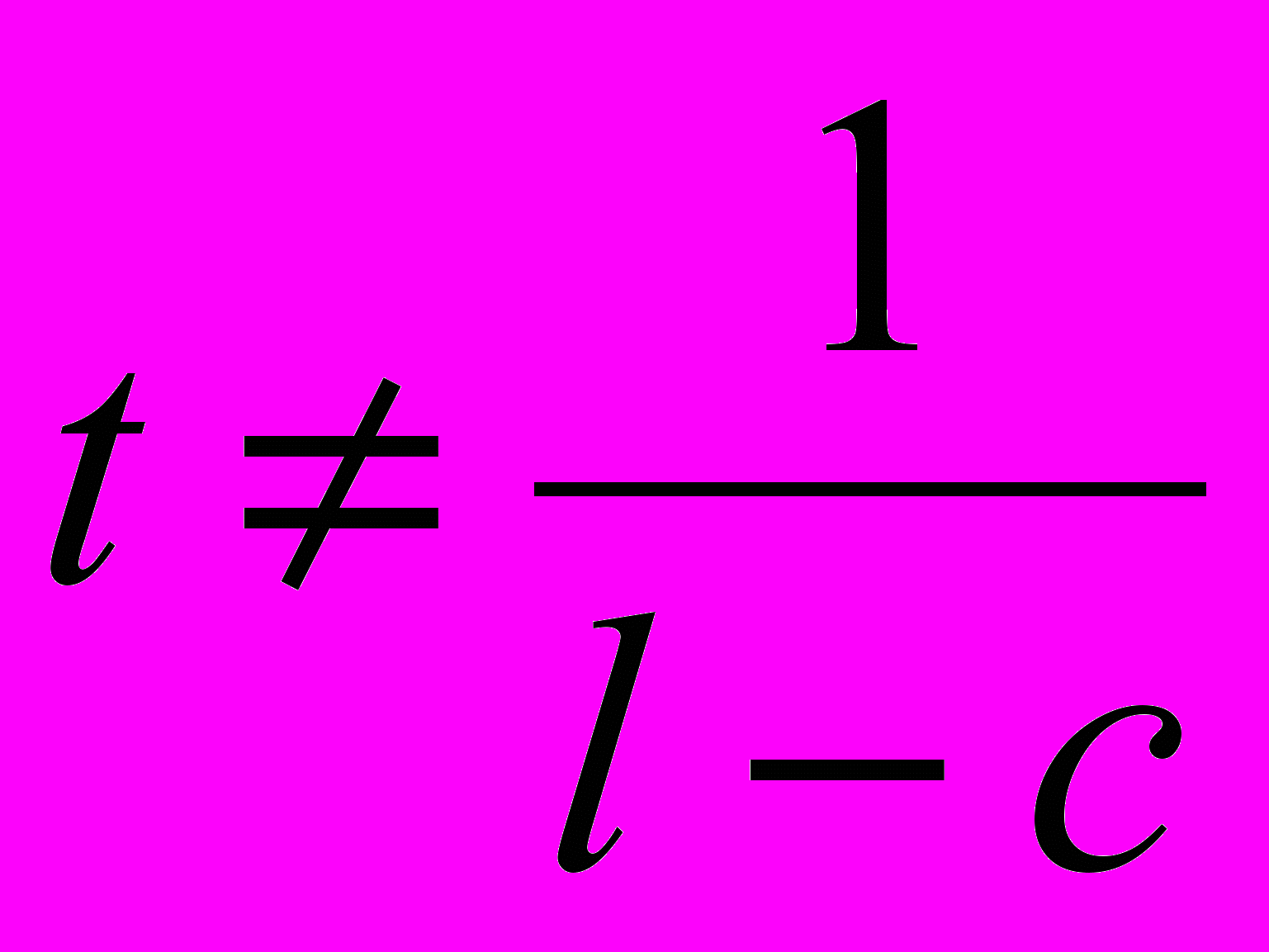 . Например, величина t может равняться 1/l – то есть весу одного варианта ответа.
. Например, величина t может равняться 1/l – то есть весу одного варианта ответа.Для того, чтобы значения оценки изменялись от 0 до 1, необходимо преобразовать f по формуле
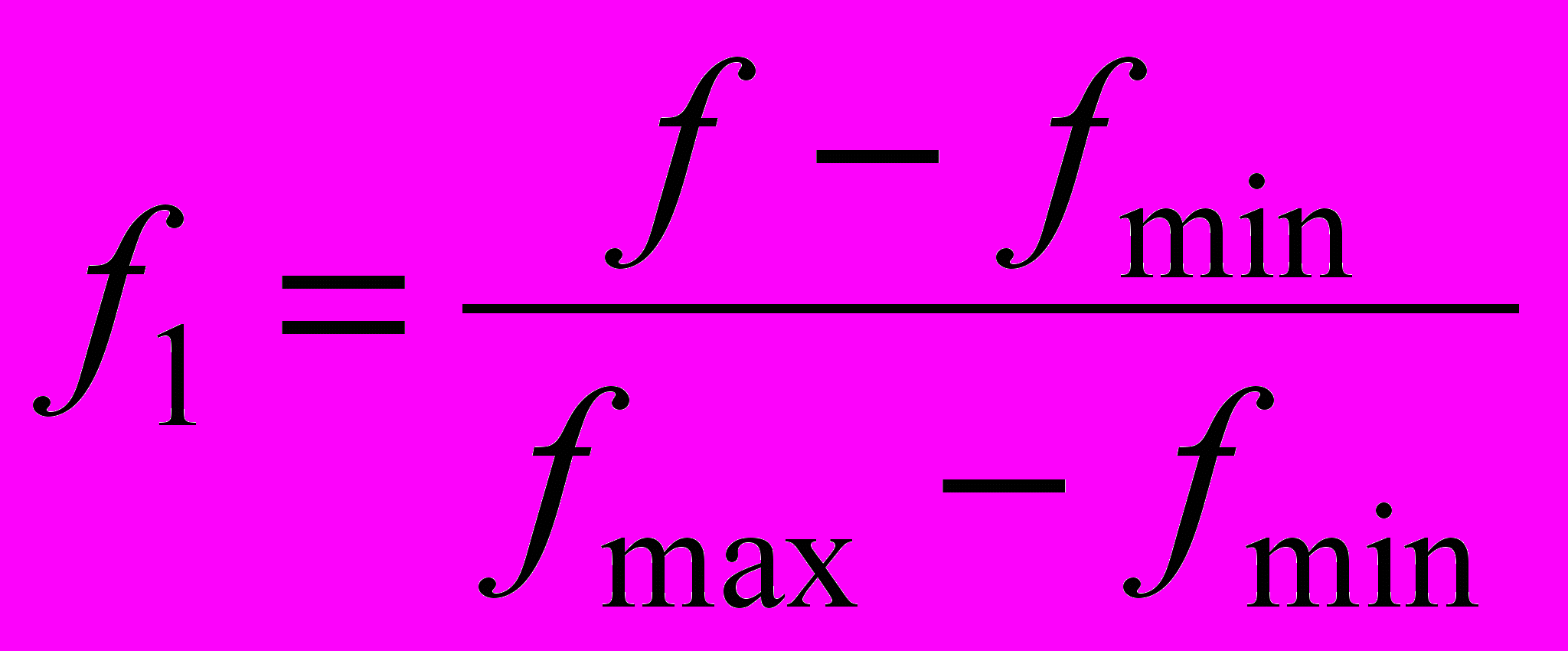 .
. Формула (2'):
В формуле (2) поощрялись недопущенные ошибки. Можно поступить противоположным образом – "наказывать" за правильные ответы, которые не были выбраны испытуемым. Поскольку правильных ответов дано a, неправильных – b, и не дано (c – a) правильных ответов, то формула примет вид:
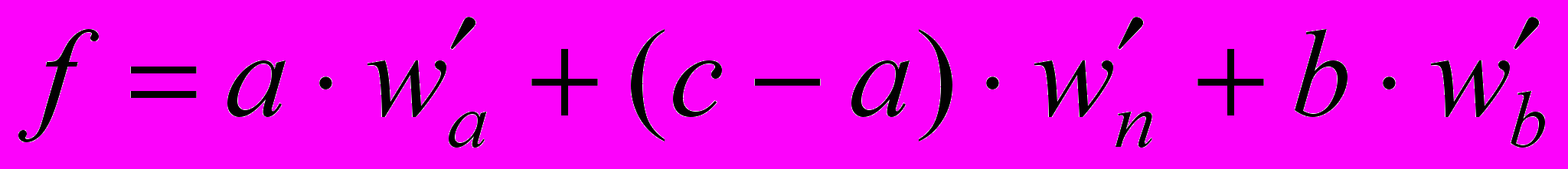 ,
,где w'n – вес правильного ответа, который не был дан. В этом случае рассуждения, аналогичные тем, которые были проведены для формулы (2), приводят к коэффициентам
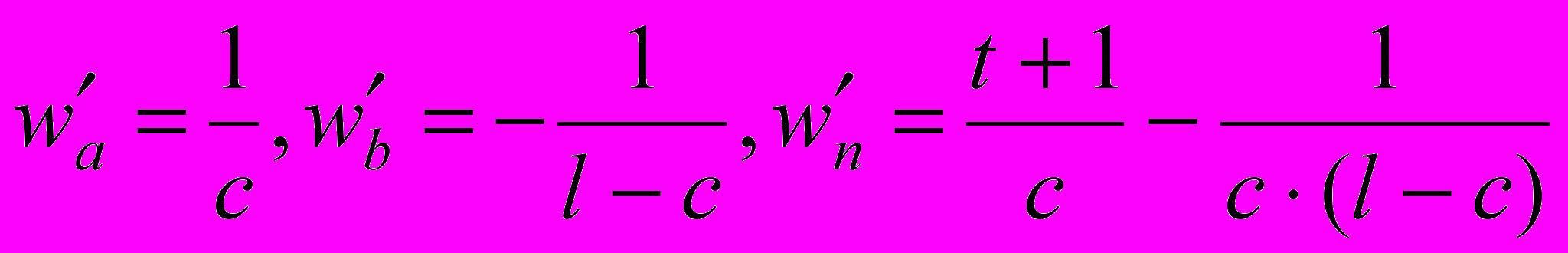 .
.Нетрудно убедиться, что при подстановке этих выражений в формулу (2') получается то же самое выражение, что при подстановке выражений wa, wb, wn в формулу (2) . То есть формулы эквивалентны, хотя и были интерпретированы различным образом.
Новый вид формулы удобен для рассуждений о количестве правильных вариантов среди предлагаемых. Если мы хотим, чтобы больший вклад в оценку вносили правильные ответы, то вес w'a по абсолютной величине должен быть больше веса w'b. Для этого должно выполняться c < l–c, откуда получаем c < l/2, то есть количество правильных ответов должно быть меньше половины всех предлагаемых вариантов. Таким образом, чем больше дистракторов мы предлагаем, тем сильнее оценка зависит от количества правильных выборов и тем меньше влияние неправильных ответов на оценку.
Формула (3):
Если бонус за недопущенные ошибки не присваивать, то вес wn должен быть нулевым. В этом случае
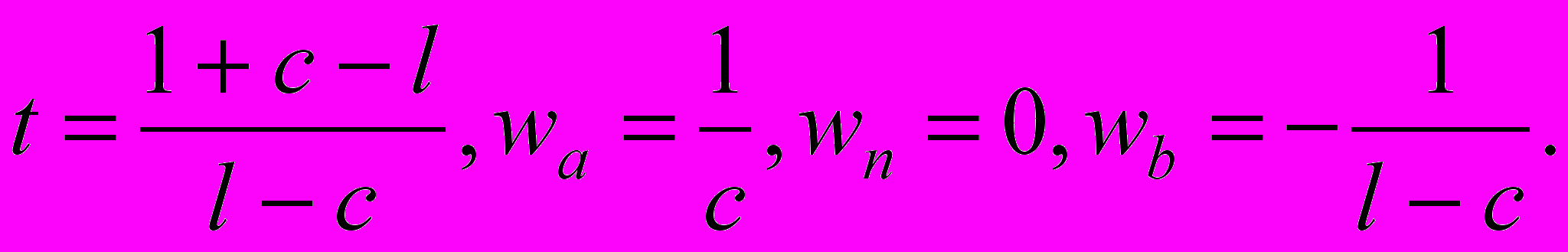
Вид формулы при этом значительно упрощается:
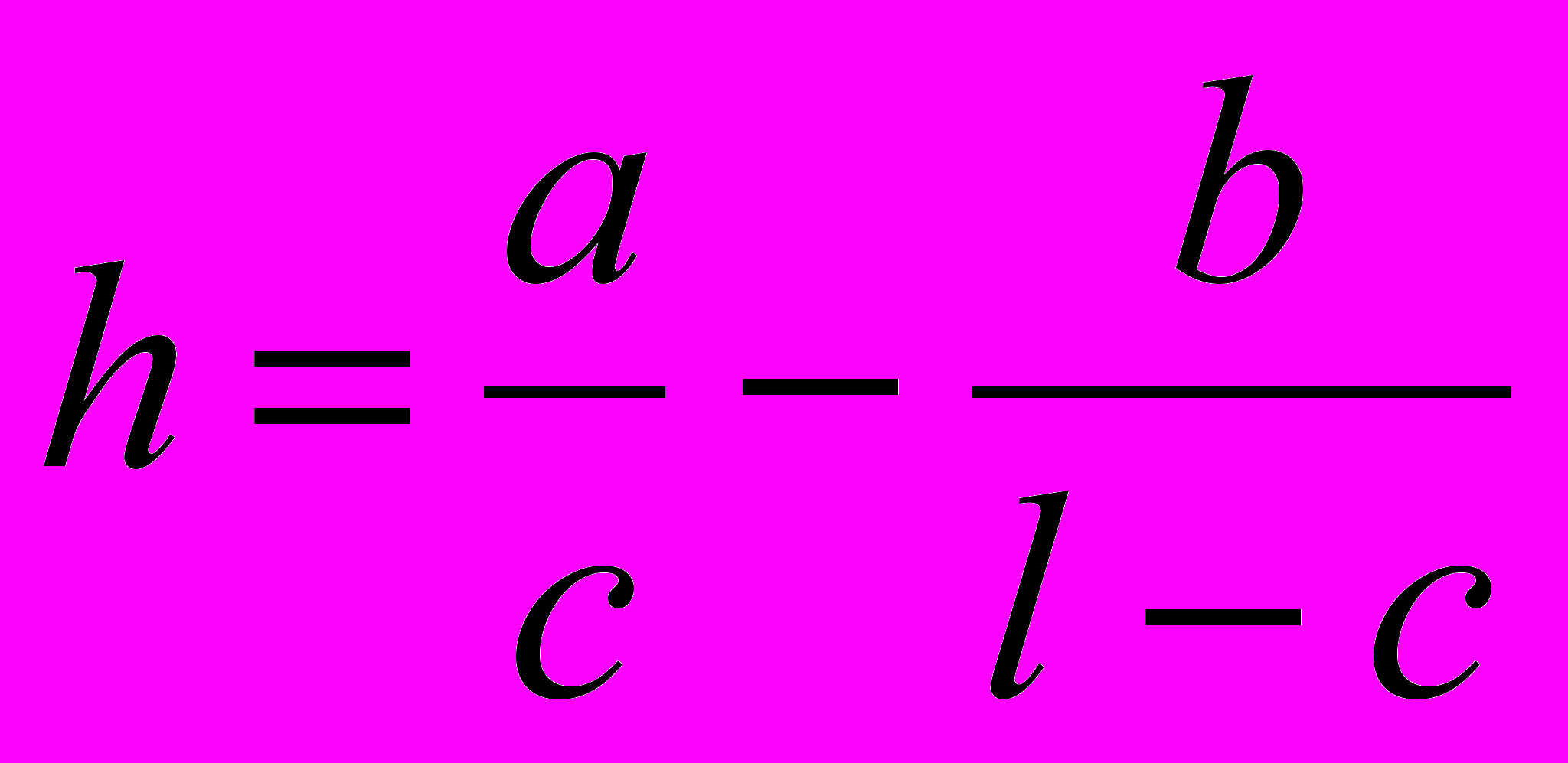 .
.Заметим, что максимальное и минимальное значения равны +1 и –1 соответственно, поэтому необходимо применить формулу для перевода значений в отрезок [0,1] (см. таблицу 2).
Формула (4):
Пусть максимальный балл равен 1 и может быть получен только в том случае, когда даны все правильные ответы и не сделано ни одной ошибки. Если же есть ошибки (b штук) или невыбранные правильные варианты (их количество равно c – a), то за каждый такой промах вычитается штраф в размере веса одного варианта. Поскольку предлагается l вариантов для выбора, то вес любого варианта считаем равным 1/l. Сумма штрафа в этом случае составит
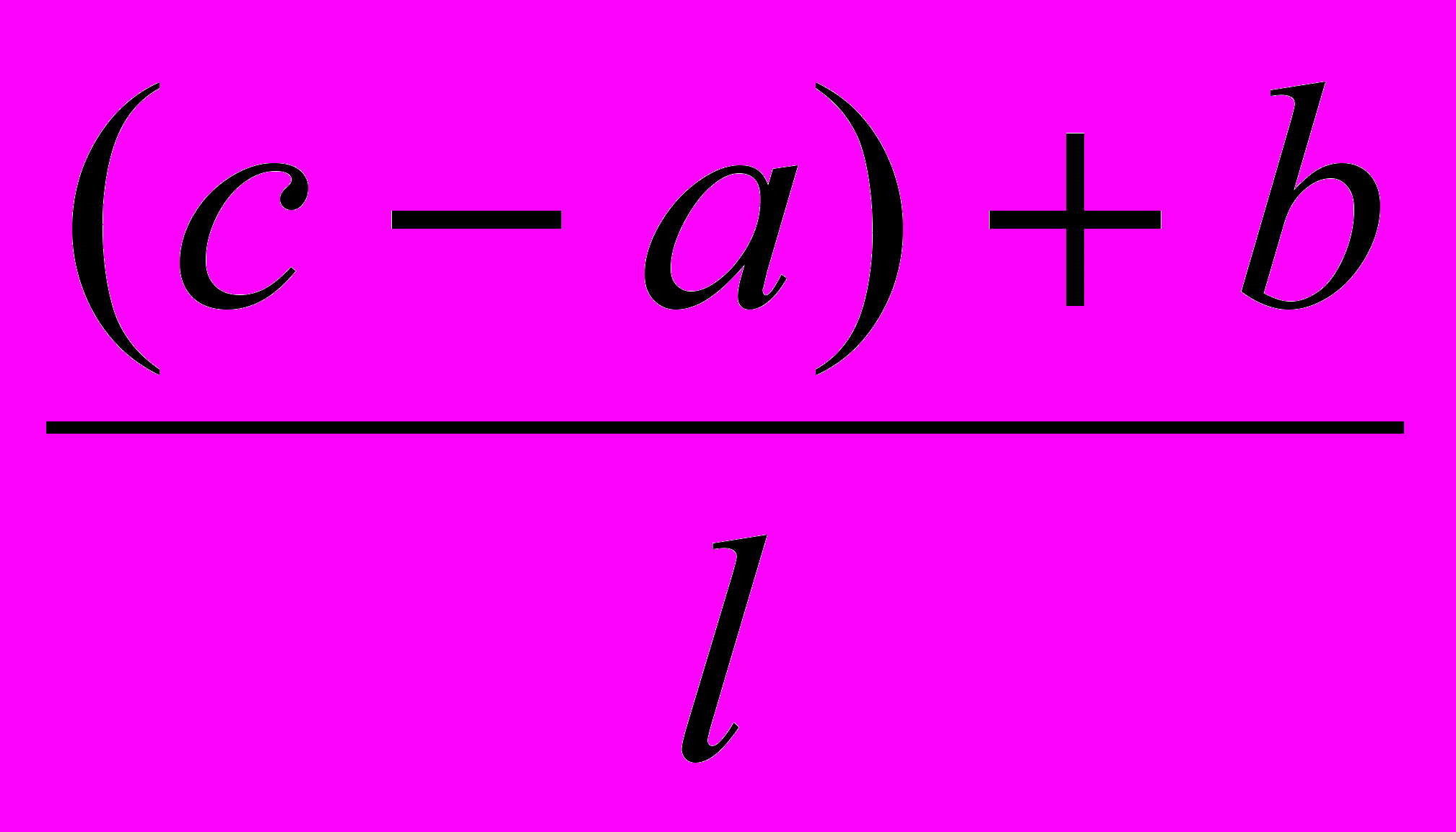 . Следовательно, балл за выполнение задания будет равен
. Следовательно, балл за выполнение задания будет равен 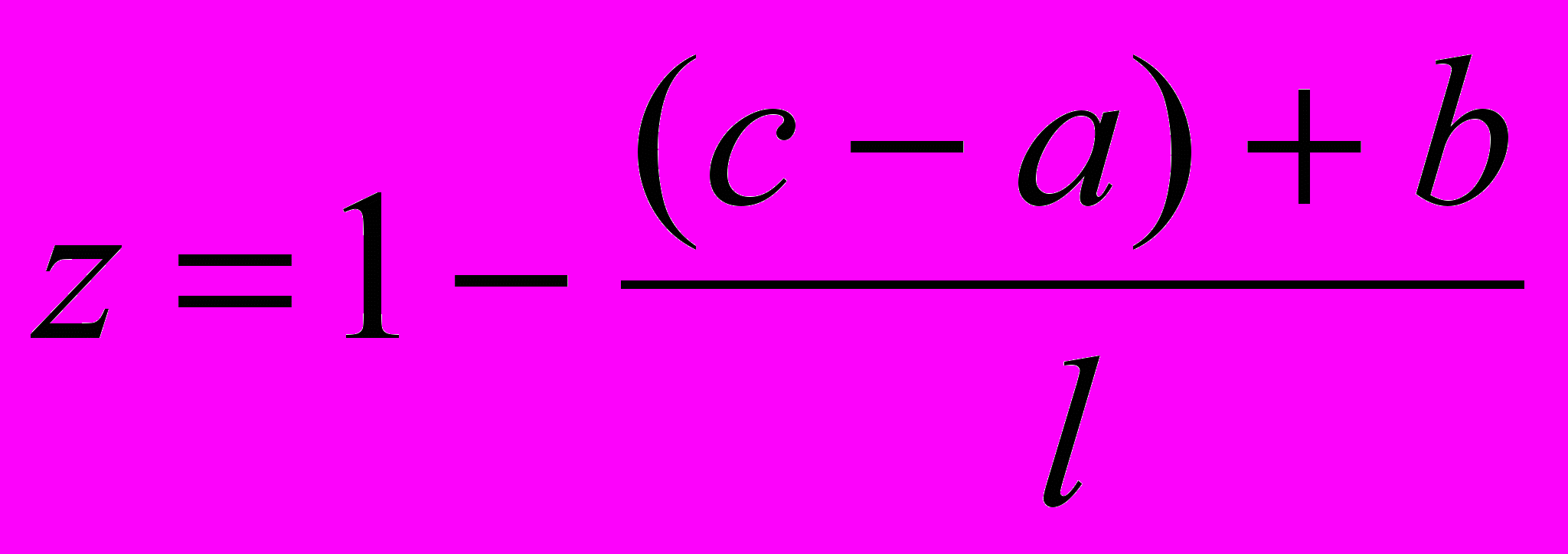 . Минимум в этом случае равен нулю и получается в случае, когда не дан ни один правильный ответ и выбраны все неправильные варианты (их количество b = l – c ).
. Минимум в этом случае равен нулю и получается в случае, когда не дан ни один правильный ответ и выбраны все неправильные варианты (их количество b = l – c ).Таблица 2
Сводка формул
| № | Формула | Примечания |
| | 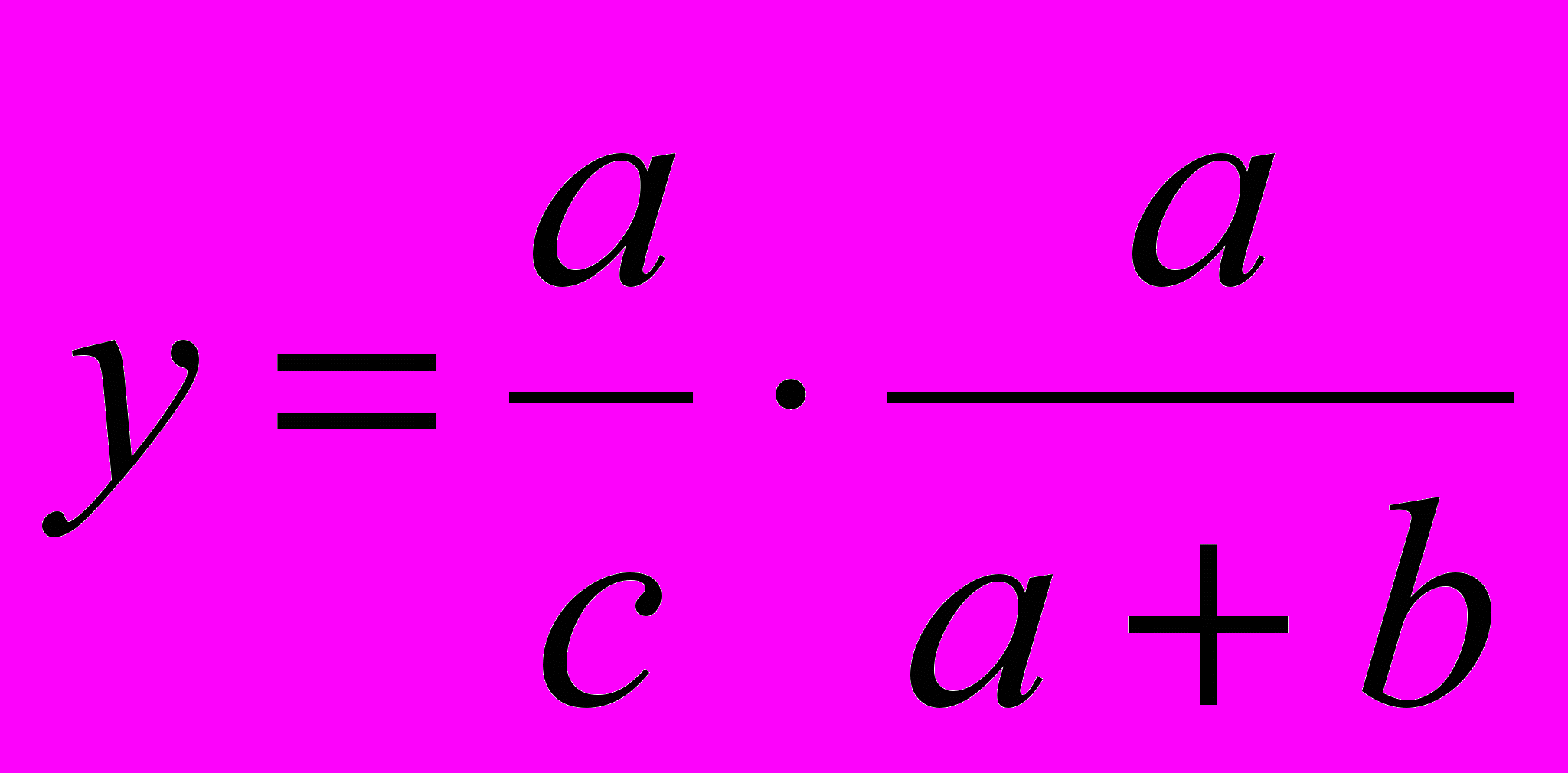 | Проблема нулевого знаменателя, малый дифференцирующий эффект |
| | 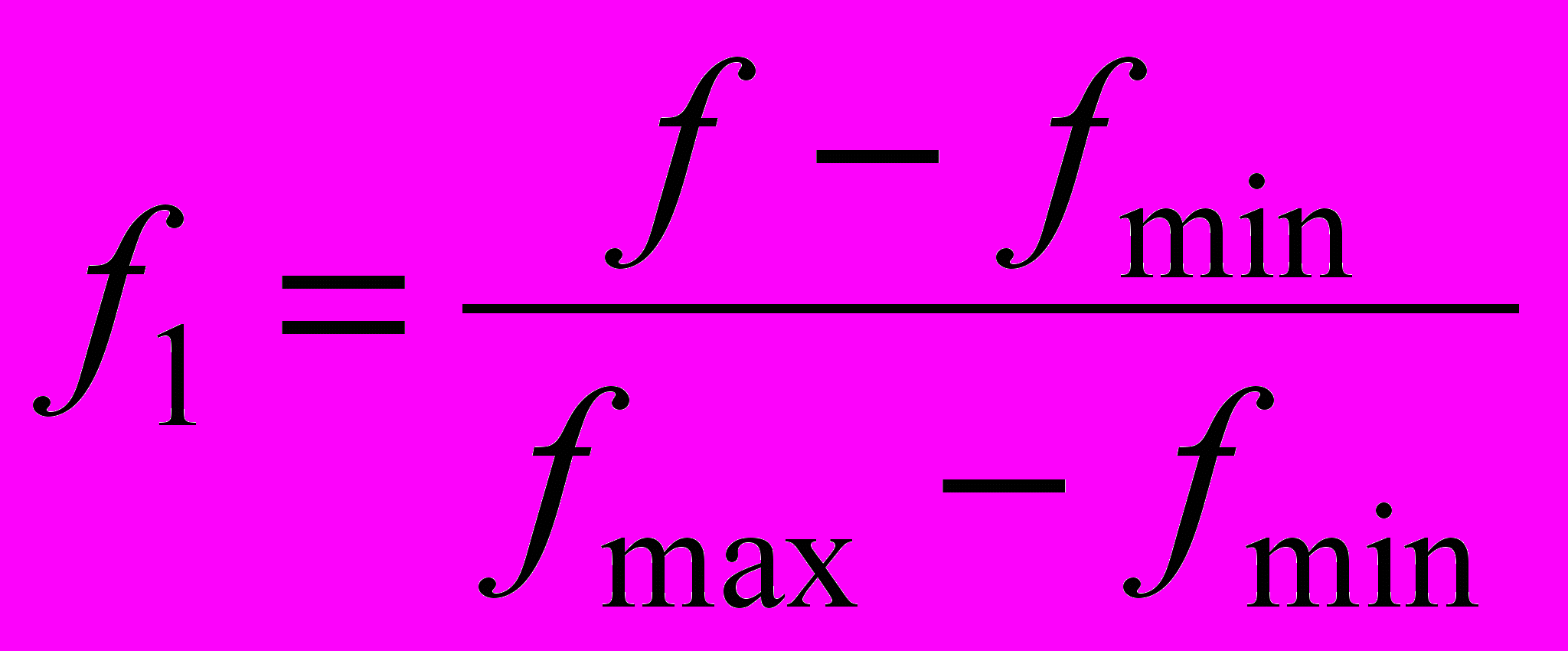 , , 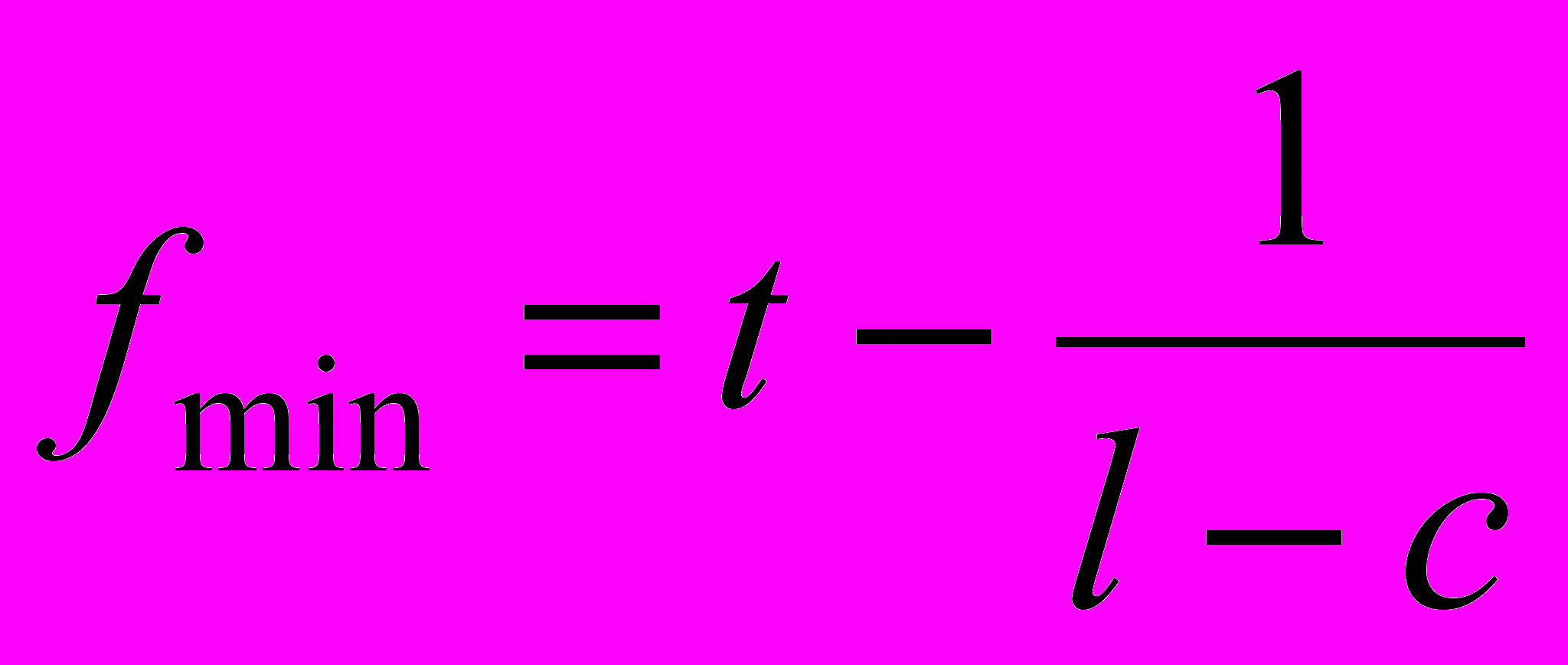 , fmax = 1, , fmax = 1,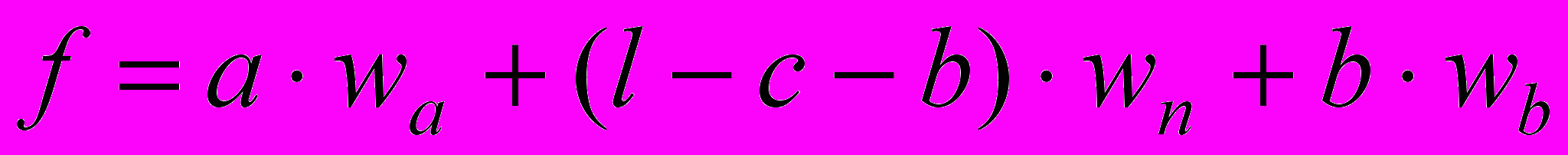 , ,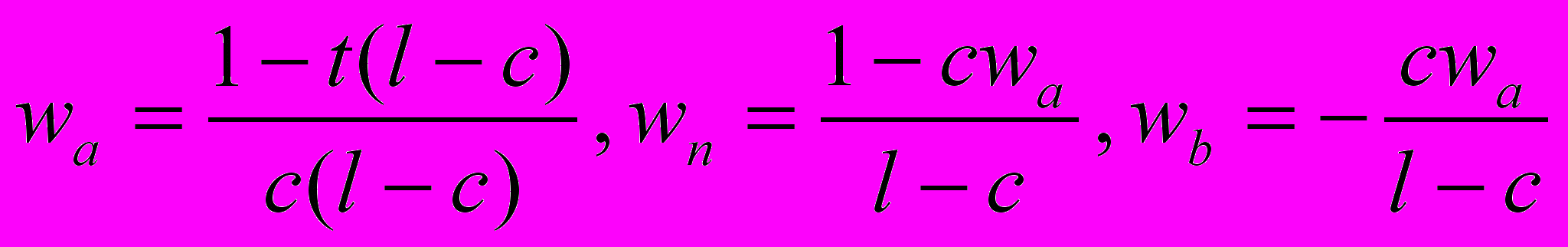 | |
| | 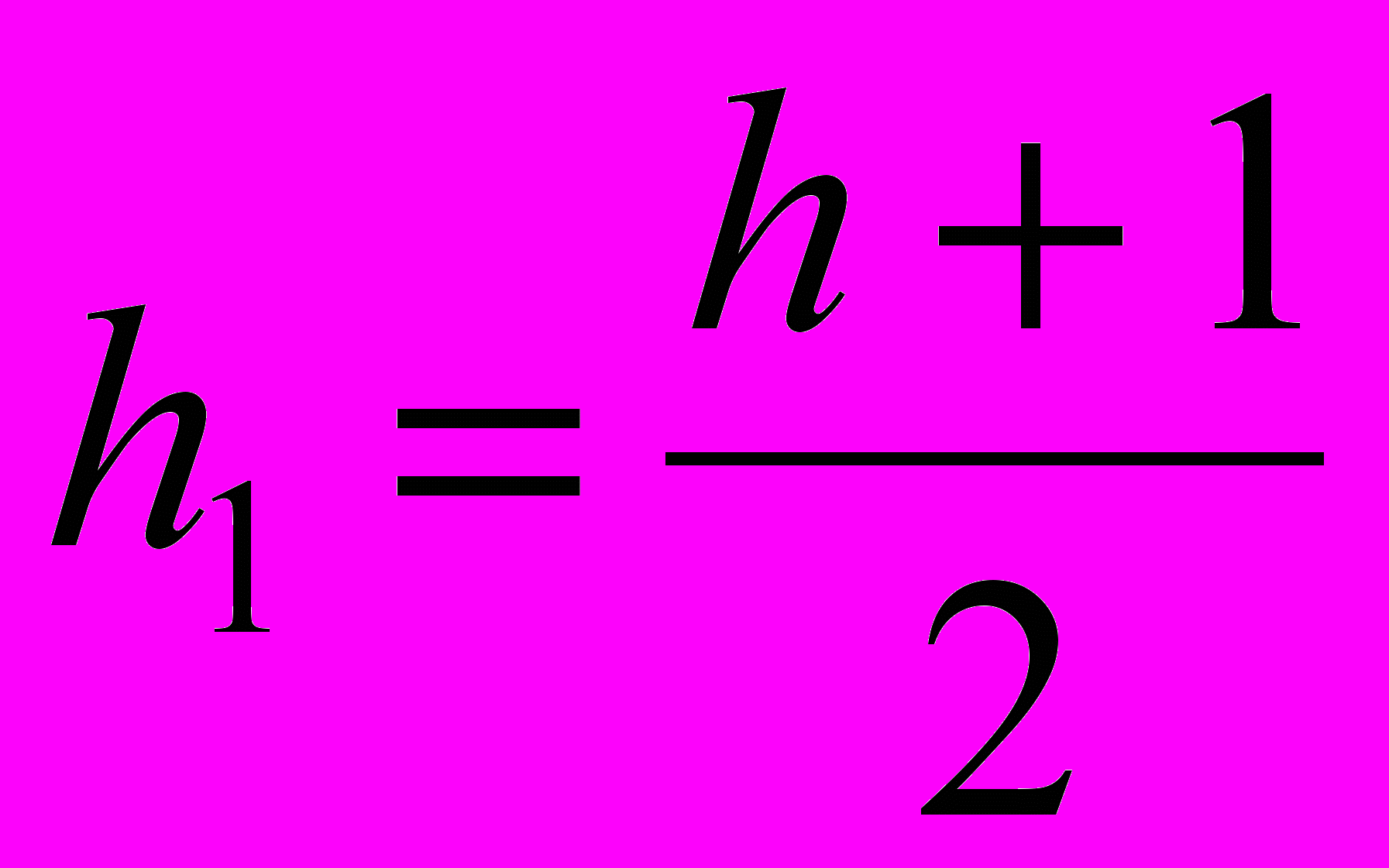 , , 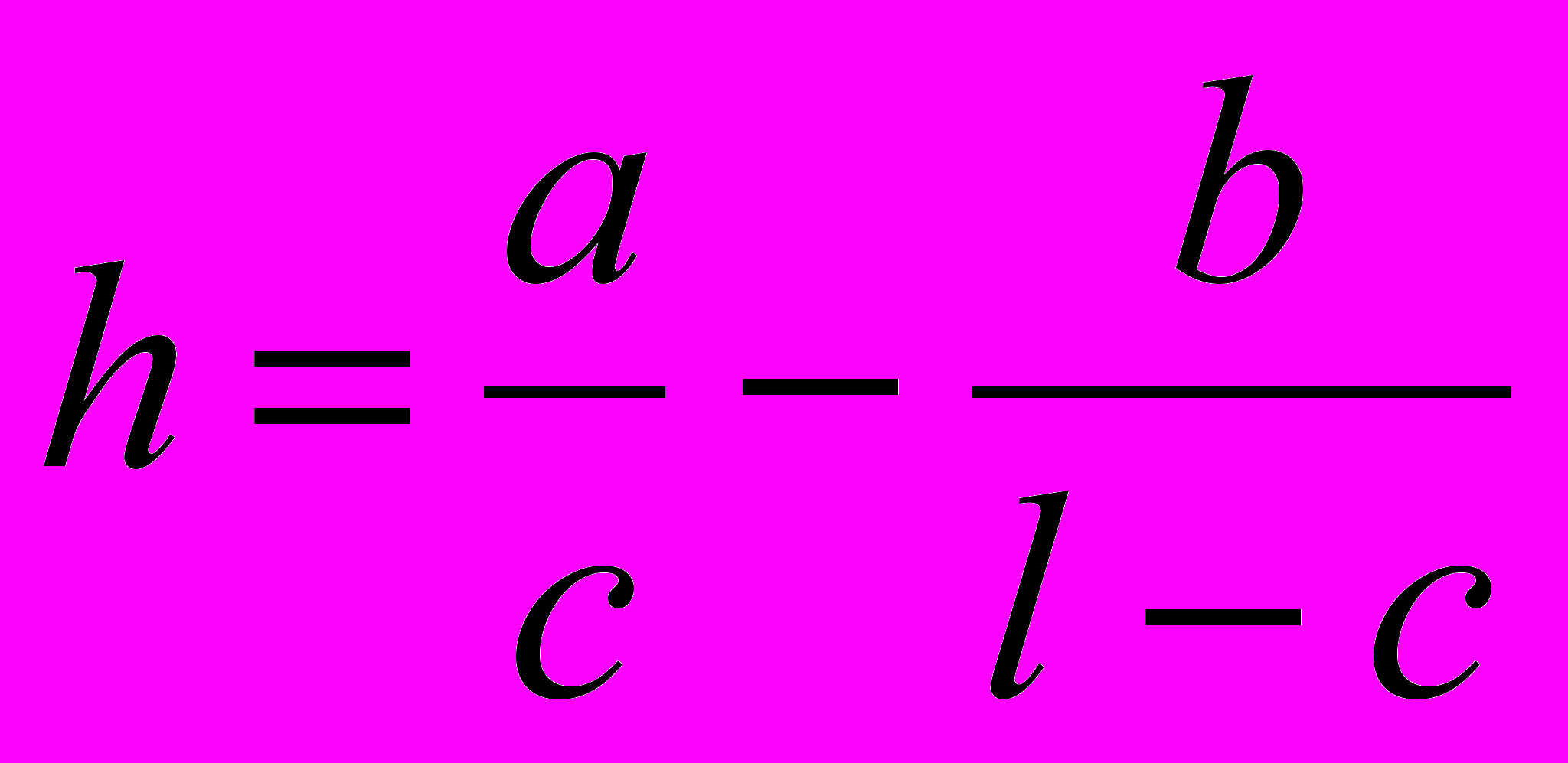 | Частный случай формулы (2) |
| | 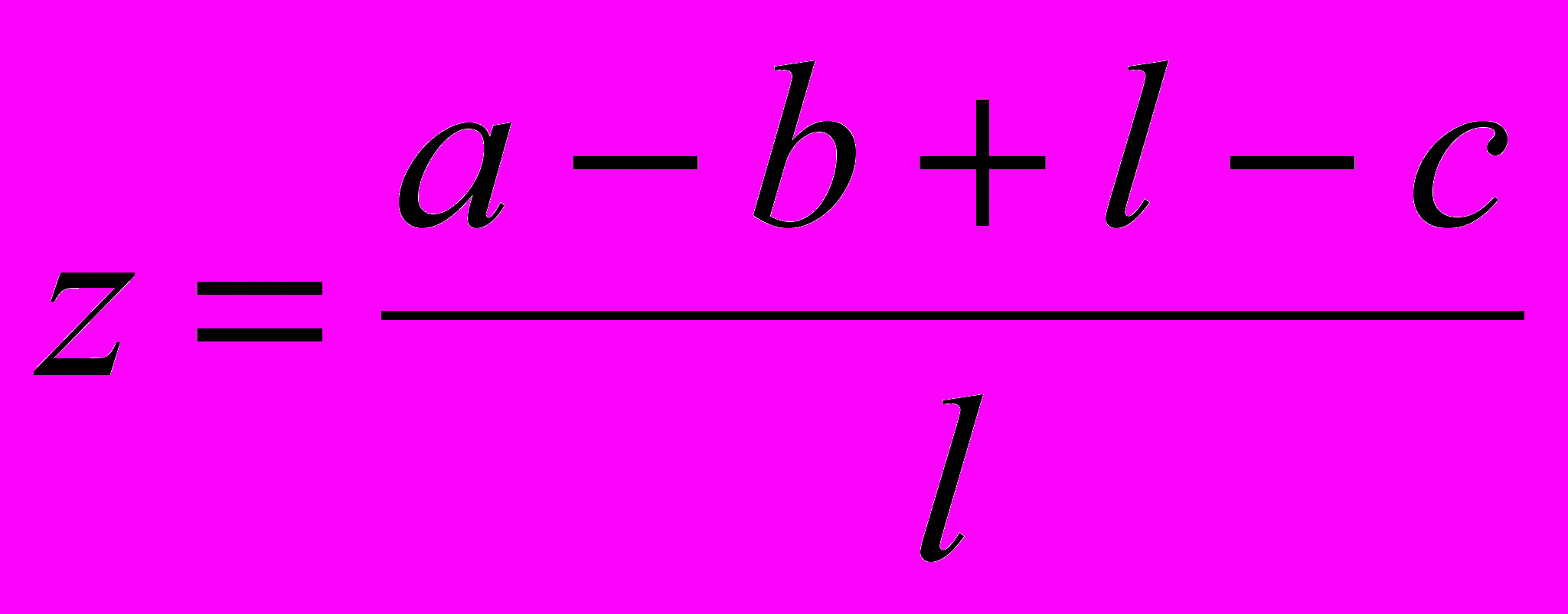 | Упрощенная модификация формулы (2) |
Зарипов В.Н., зав. каф. физиологии человека и животных (1);
Щаницина С. В., ст. преп. кафедры вычислительной
и прикладной математики (2-4).
