Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материала

Рабочая учебная программа

Содержание 0ху воспользуемся формулами. Задание №4 Задание №5 Первый столбец 2 в первой строке и 1 Третий столбец Задание №6 I строки умножаем на (-2) III строки делим на 3 IV строки делим на (-4) Задание №7 Задание №8 A линейным надо проверить, выполняются ли эти равенства. Проверим, является ли оператор A A имеет собственное значение λ=0 Задание №9 Задание №10

Подобный материал:

• Рабочая программа, методические указания по выполнению курсовой работы и контрольные, 1000.11kb.
• Программа и контрольные задания по учебной дисциплине, 858.36kb.
• Программа и контрольные задания по учебной дисциплине «эконометрика» для студентов, 555.04kb.
• Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
• Программа и контрольные задания по учебной дисциплине «трудовое право» для студентов, 805.51kb.
• Программа и контрольные задания по учебной дисциплине «отечественная культура» для, 729.22kb.
• Рабочая программа По дисциплине «Стратегическое управление организацией» Для курса, 197.74kb.
• Программа и контрольные задания по учебной дисциплине «отечественная история» для студентов, 583.38kb.
• Программа, контрольные задания и тематика курсовых работ по учебной дисциплине основы, 557.3kb.
• Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.

ГИПЕРБОЛА

Если уравнение имеет вид >0, >0

кривая называется гиперболой ( каноническое уравнение гиперболы)

Точка - центр гиперболы, Точки (±,0)-вершины гиперболы, При =0, =0,

Прямые = ± асимптоты гиперболы.

, >0. Точки (-,0) и (,0) фокусы гиперболы.



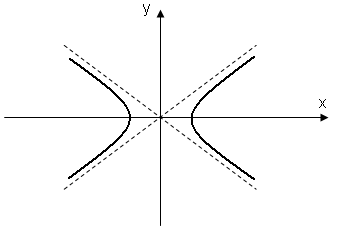
ПАРАБОЛА

Если уравнение имеет вид: , где >0, то линия называется параболой ( каноническое уравнение параболы)

,-координаты вершины параболы; При ==0 (,0 ) - фокус параболы ; прямая - директриса параболы.

На плоскости может быть введена не только декартова прямоугольная, но и полярная система координат.

Зададим точку О -полюс, ось Z содержащую точку О и единицу длины оси Z. Возьмем произвольную точку М плоскости. Её положение на плоскости определяется двумя числами – расстоянием r от О до М (полярный радиус) и отсчитываемым против часовой стрелки углом φ между лучом OM и лучом оси (полярный угол). Если поместить начало координат декартовой прямоугольной системы в полюс, то координаты будут связаны следующим образом.



Пример 1. Пусть в задаче №3

Построим заданную линию по точкам в полярной системе координат. В начале определим область допустимых значений (ОДЗ) независимой переменной φ. По определению полярной системы координат и .Точке r = 0 соответствует полюс 0.

По условию задач угол φ может меняться от 0 до 2π. Поэтому наибольшие размеры ОДЗ таковы . При этом r>0 (r0), т.к. числитель соответствующей дроби 4>0. отсюда знаменатель этой дроби также должен удовлетворять неравенству 2-3cos φ > 0 или cos φ < 2/3. Решаем последнее неравенство cos φ = 2/3 0,667;

0,667 +2πk, kN; φ =.

В промежуток попадают два значения φ₁= и φ₂ = -. Отсюда для cos φ<2/3.

Следовательно, допустимые значения φ принадлежат промежутку от 3π/8 до 13π/8, т.е. ОДЗ: . Результаты расчетов заносим в таблицу

φ	3π/8	π/2	5π/8	6π/8	7π/8	π	9π/8	10π/8	11π/8	12π/8	13π/8
cosφ	0.38	0	-0.38	-0.71	-0.92	-1	-0.92	-0.71	-0.38	0	0.38
r	4.75	2	1.27	0.97	0.84	0.8	0.84	0.97	1.27	2	4.75

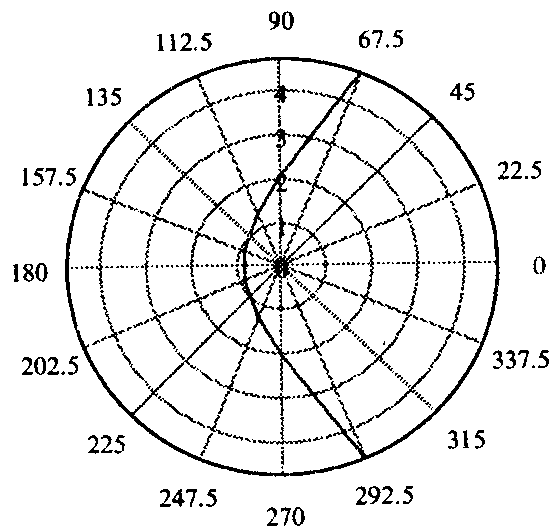Строим чертеж ,откладывая на луче , проведенном из полюса О под определенным углом φ, соответствующие значения радиус-вектора r из таблицы


rl(φ)


Для перехода к системе 0ху воспользуемся формулами. Имеем, следовательно - r (2-3cos φ)=4,



Определяем ОДЗ для х. Из ОДЗ : для φ >0.

Следовательно, 3х+4>0. Отсюда ОДЗ: х>-4/3. Возводим правую и левую части равенства в квадрат и выделяем полный квадрат для переменной х:

4х²+4у²=9х²+24х+16; (5х²+24х)-4у²+16=0;

5(х²+2;

(х+12/5)²-4/5у²-144/25+16/5=0; (х+12/5)²-4у²/5=64/25



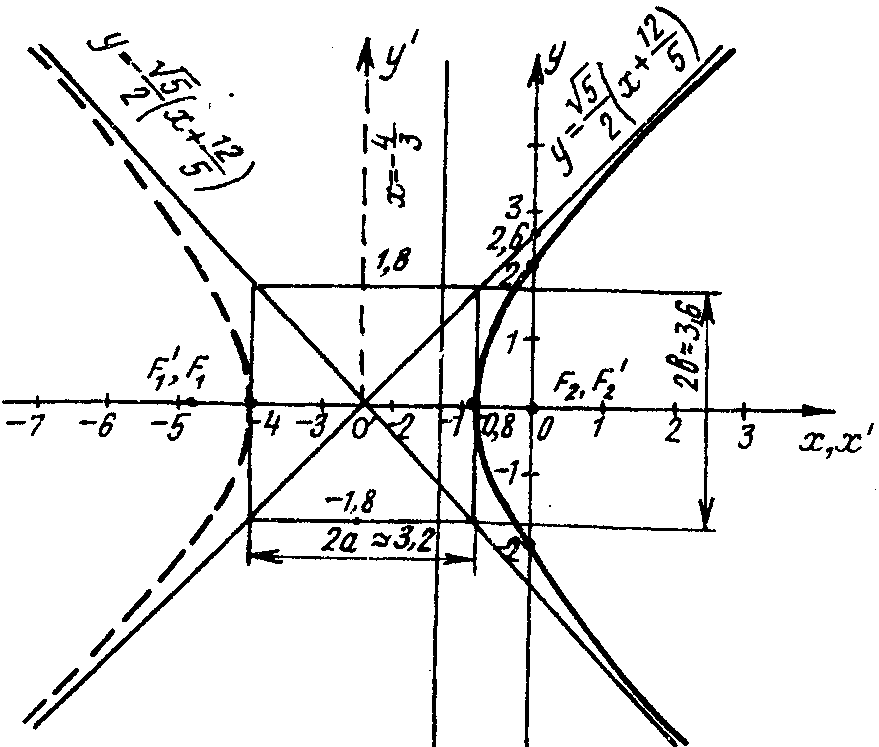
Окончательно получаем уравнение гиперболы х > -

с центром в точке С(-12/5;0), а = 8/5, b = 4/.

Находим координаты фокусов, уравнения асимптот и эксцентриситет. Для этого систему координат 0ху параллельно перенесем в точку . Заменяя переменные =х+12/5, =у, получим в новой системе координат уравнение гиперболы с центром в



Получим координаты фокусов, уравнения асимптот и эксцентриситет гиперболы:





или ,

Переходим в старую систему координат. Имеем: .

Следовательно: F₁(x;y)=F₁(=F₁(-24/5;0);

F₂(0;0), у = +

Совмещаем начало О системы координат Оху с полюсом, отмечаем координаты фокусов F₁ и F₂, проводим асимптоты и строим пунктиром левую ветвь гиперболы, т.к. точки гиперболы в полуплоскости слева от прямой х=-4/3 не удовлетворяют ОДЗ х>-4/3.




В случае если уравнение не подходит под один из перечисленных выше частных случаев линии второго порядка требование задачи «назвать линию» следует опустить.

ЗАДАНИЕ №4

Для решения задачи № 4 следует иметь понятие о базисе.

Система из n линейно независимых векторов в n-мерном пространстве называется базисом. Векторы называются линейно независимыми, если равенство

(линейная комбинация этих векторов равна 0) выполняется только при нулевых значениях коэффициентов – всех при i=1,2…n.

Если это равенство имеет место при условии, что хотя бы один из коэффициентов отличен от нуля, то система векторов называется линейно зависимой.

В n-мерном пространстве линейно независимая система векторов не может содержать более n векторов.

Пусть задана система из n линейных уравнений с n неизвестными



Матрица системы – набор из чисел-коэффициентов системы, так как число строк матрицы равно числу столбцов матрица называется квадратной.



Её определитель (для случая, когда n=3):



-определитель разложен по первой строке. Как определяются определители высших порядков, можно узнать в указанных ниже учебниках или в следующем разделе.

Итак, если определитель системы , то система имеет единственное решение , которое можно найти по формулам Крамера



Где определитель матрицы системы, а определитель матрицы, полученной из матрицы системы А заменой i-го столбца на столбец свободных членов .

Пример 1. Решим задачу разложения вектора по базису:

Пусть даны вектора

Решение.: Покажем в начале, что векторы и образуют базис. Система векторов образует базис, если эти векторы линейно независимы, а соответствующее векторное уравнение





Обращается в тождество только при λ₁=λ₂=λ₃=0.

Используя координаты векторов , составим систему линейных уравнений, эквивалентную векторному уравнению





Вычисляем определитель Δ данной системы

=1(-1)-1(-2)=1.

Так как Δ 0, то система имеет только нулевое решение (λ₁,λ₂,λ₃) =(0,0,0). Это следует из того факта, что при b_i =0 все определители при неизвестных в формулах Крамера равны нулю Δ₁ = Δ₂ =Δ₃ = 0.

Следовательно, векторы образуют базис.

Найдем координаты вектора в базисе . Четыре вектора в трехмерном пространстве всегда линейно зависимы, т.е. вектор есть линейная комбинация векторов

.


Аналогично предыдущему случаю составим систему уравнений для определения координат λ₁,λ₂,λ₃ вектора в базисе




Определитель системы совпадает с определителем системы и не равен нулю Δ=1 0. Следовательно, система имеет единственное решение. По формулам находим λ₁,λ₂ и λ₃









λ₁=Δ₁/Δ=-2/1=-2, λ₂=Δ₂/Δ=3/1=3, λ₃=Δ₃/Δ=-4/1=-4,

Итак, разложение вектора по базису имеет вид:




Если векторы заданы в базисе , то в этом базисе вектор имеет координаты (2;1;3).

Студенту рекомендуется самостоятельно нарисовать векторы в пространстве R³ и сравнить полученные значения λ_i cо значениями, полученными графически.

ЗАДАНИЕ №5

Задача №5 – это задача нахождения обратной матрицы.

Какие операции можно выполнить над матрицами?

Сложение матриц:



Умножение матрицы на число:



Умножение матриц:



Транспонирование матриц:



То есть элемент матрицы находящийся в позиции совпадает с элементом матрицы А, находящимся в позиции . Таким образом строки матрицы А переходят в столбцы , а столбцы– в строки.

Нахождение определителя (для квадратных матриц):

Для нахождения определителя третьего порядка мы пользовались в предыдущих задачах формулой:

,

Т.е. умножили элементы первой строки на определители, которые останутся от исходного определителя третьего порядка, если вычеркнуть этот элемент вместе со своей строкой и столбцом.

Определителем матрицы n-го порядка

называется число D



Где – элементы первой строки, знак совпадает со знаком

– минор – то есть определитель, матрицы порядка n-1, полученной вычеркиванием i-ой строки и j-го столбца.

Таким образом

– формула разложения определителя по i-ой строке.

Число назовем алгебраическим дополнением элемента . И тогда формулу определителя можно написать в виде:



Нахождение обратной матрицы (если ):

, где – алгебраическое дополнение элемента

Для обратной матрицы

, где Е – единичная матрица

.

Можно построить обратную матрицу методом Жордана. Для этого следует составить расширенную матрицу (А/Е). Если подвергнуть строки этой матрицы элементарным преобразованиям (сложение и умножение на число) с целью получить на месте матрицы А единичную матрицу Е, то на месте матрицы Е получится – обратная к А.

Пример 1. Вычислим матрицу обратную матрице .

Решение. Вычисляем определитель матрицы А



Следовательно, матрица А^-1 существует.

Алгебраические дополнения элементов а_ji исходной матрицы вычисляем по столбцам матрицы А







Записываем их в строки матрицы А^-1



Делаем проверку:



, ,



,






В самом деле:

Проверим наши вычисления по методу Жордана.

Составим расширенную матрицу

B =

Первый столбец

Наша цель – чтобы первый столбец выглядел так , т.е. надо уничтожить тройку во второй строке. Для этого первую строку умножаем на 3 и вычитаем из второй



Второй столбец

Теперь надо, сделать второй столбец таким же, как второй столбец матрицы Е, т.е надо чтобы второй столбец был таким .

Для этого вторую строку умножим на

.

Теперь надо уничтожить 2 в первой строке и 1 в третьей строке.

Умножаем вторую строку на 2 и вычитаем из первой. Результат записываем на место первой строки. Вторую строку оставляем на своем месте. Из третьей строки вычитаем вторую строку, результат записываем на место третьей строки.

.

Третий столбец

Третий столбец у единичной матрицы должен быть таким , то есть все три строки придется менять. Разделим третью строку на

.

Теперь уничтожим в первой строке. Для этого третью строку умножим на и вычтем из первой. Результат запишем на место первой строки.



Теперь в третьем столбце от столбца единичной матрицы отличается только элемент второй строки. Это . Чтобы на этом месте был ноль, добавим ко второй строке третью, умноженную на . Результат впишем на место второй строки.

.

Теперь сократим все дроби, где это возможно

.

Действительно, мы получили матрицу .

ЗАДАНИЕ №6


Задача №6 – задача решения системы линейных уравнений методом Гаусса.

Пусть задана система четырех линейных алгебраических уравнений с четырьмя неизвестными х₁,х₂,х₃,х₄




Требуется найти решение (х₁,х₂,х₃,х₄) этой системы.

Перед решением системы исследуем её на совместность. По теореме Кронекера – Капелли для совместности системы необходимо и достаточно, чтобы ранг основной А и расширенной А₁ матриц совпадали



r(A)=r(A₁).

Система будет определенной, если ранг совместной системы равен числу неизвестных n

r(A)=n=4


Если , то первое уравнение системы заменяем на уравнение в котором а_i1=1

По методу Гаусса с помощью эквивалентных преобразований над строками расширенную матрицу А₁ системы надо привести к матрице




В которой основная матрица А принимает треугольный вид , т.е. на главной диагонали матрицы А все элементы равны единице, ниже – нулю. На этом прямой ход метода Гаусса заканчивается.

В процессе обратного хода из матрицы находим значения неизвестных х_i, начиная с последней x₄=b₄₅ и до первой x₁=b₁₅

Одновременно с прямым ходом по методу Гаусса можно определить ранги r(A) и r(A₁)

Пример 1. Пусть задана система



Решение: Так как а₁₁=0, I и IV(см. выше) уравнения системы меняем местами и записываем расширенную матрицу полученной системы



Выполняем последовательно следующие преобразования. В матрице каждый элемент I строки умножаем на (-2) и прибавляем к соответствующим элементам II строки; затем элементы I строки умножаем на (-1) и складываем с соответствующими элементами III строки. В результате получаем:



В полученной матрице элементы III строки делим на 3 и затем элементы II строки умножаем на (-1) и складываем с элементами соответственно III и IV строк:



Элементы III и IV строк нашей матрицы меняем местами; элементы III строки делим на (-1), затем умножаем на (3) и складываем с элементами IV строки



В этой матрице элементы IV строки делим на (-4)



Полученной матрице соответствует система:



Из последнего уравнения системы х₄=2; из III уравнения х₃=2+х₄=2+2=4; из II уравнения х₂=18-2х₄-2х₃= из I уравнения x₁=-6+2x₂+x₄=-6+2·6+2=8

Итак, решение системы равно (х₁,х₂,х₃,х₄)=(8;6;4;2).

Для избежания ошибок в решении студенту рекомендуется сделать проверку, подставив найденное решение (х₁,х₂,х₃,х₄) в каждое уравнение системы.

Найдем ранги и




Таким образом, определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали.

Поскольку отличный от нуля определитель квадратной матрицы имеет размерность 4 х 4, то ранг матрицы равен r(А)=4.

В матрице вычеркиваем IV столбец и определяем ранг матрицы в приведенном к треугольному виде:



Отсюда r()= 4.

Следовательно система совместна и определена.

ЗАДАНИЕ №7

Задача №7: Привести квадратичную форму к каноническому виду; найти ортонормированный базис, в котором матрица квадратичной формы имеет диагональный вид; найти матрицу перехода к ортонормированному базису.

Квадратичной формой действительных переменных называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени. Если - квадратичная форма переменных , а λ – какое-то действительное число, то .

Если n=2, то .

Матрица у которой , называется матрицей квадратичной формы . Т.к. А – симметричная матрица, то корни λ₁ и λ₂ характеристического уравнения являются действительными числами.

Пусть и



нормированные собственные векторы, соответствующие характеристическим числам λ₁ и λ₂ в ортонормированном базисе . В свою очередь векторы образуют ортонормированный базис. Матрица



Является матрицей перехода от базиса к базису . Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид:





Преобразовав с помощью этих формул квадратичную форму , (не содержащую членов с произведениями).

говорят, что форма приведена к каноническому виду.

Пример 1. Приведем к каноническому виду квадратичную форму .

; ; .

Составим характеристическое уравнение

=0 или .

; .

Определим собственные векторы

I)





;

Полагая что , получим , то есть собственный вектор .

II).





Полагая что , получим , то есть собственный вектор .

Чтобы нормировать векторы u и v, следует принять .

Итак, мы нашли нормированные собственные векторы



где - ортонормированный базис, в котором матрица квадратичной формы имеет диагональный вид.

Матрица перехода от ортонормированного базиса к ортонормированному базису имеет вид:

B=

Канонический вид квадратичной формы



ЗАДАНИЕ №8

Если в линейном пространстве R каждому вектору по некоторому правилу поставлен в соответствие вектор , то говорят, что в пространстве R задан оператор A. Оператор A называется линейным, если для любых векторов и и любого действительного числа λ выполняются равенства:



Значит, для того, чтобы проверить, является ли оператор A линейным надо проверить, выполняются ли эти равенства. Проверим, является ли оператор A линейным в R^{3 -}

Возьмем два вектора и



То есть оператор A является линейным, найдем его матрицу.



Первая координата произведения получается умножением первой строки на столбец , то есть , значит , ,

Вторая координата произведения:





Третья координата произведения:





Итак, матрица оператора



Найдем собственные значения линейного оператора:



(1-λ)·(1-λ)²-1·1=0

(1-λ)³=1

1-λ=1

λ=0

Оператор A имеет собственное значение λ=0 кратности 3.

Для определения координат собственного вектора получаем систему уравнений:




положив

получим:


Собственному числу соответствует собственный вектор

ЗАДАНИЕ №9

Пример 1. Выполнить действия над комплексными числами в алгебраической форме.

Решение: Алгебраической формой комплексного числа называется следующий его вид z=x+iy. Действия над комплексными числами в алгебраической форме производятся как над многочленами вида a+xb. Специфическим приёмом деления комплексного числа на комплексное число является домножение и числителя и знаменателя на комплексно сопряжённое знаменателю число. В результате частное не изменится, но делитель будет вещественным.

Заметим что



Пример 2. Найти тригонометрическую форму числа . Найти:

Решение :Выражение вида называется тригонометрической формой числа z, где модулем z называют , аргументом z – угол между радиус-вектором точки z и положительным направлением оси Ох.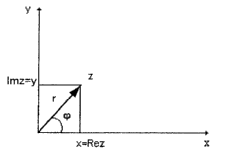




Очевидно, что если |z|r, arg z , то действительная часть числа z Re z x r cos, а мнимая часть числа z Jm z y  r sin 

Таким образом, в терминах модуля и аргумента комплексное число можно представить в виде

Для определения тригонометрической формы комплексного числа z найдём r,



Та как sin и cos угла отрицательны, делаем вывод, что угол находится в III четверти

Вычислим по формуле Муавра



1²⁰=1




Пример 3. Решить уравнение

Известно, что корнем n-степени из числа z называется любое число , такое, что и ω имеет n различных значений.

Решение: если число z представить в тригонометрической форме

то значения можно представить формулой

Поскольку все одинаковы, а аргументы отличаются на 2П/n, то значения на комплексной плоскости располагаются в вершинах правильного n угольника. Величина называется главным значением корня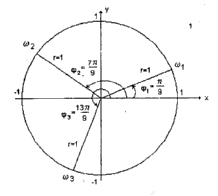






Итак, корнями уравнения будут три единичных вектора, расположенных под углом в 120 градусов друг к другу.

ЗАДАНИЕ №10

Для решения контрольной работы №2 по математике или контрольной работы №1 по математическому анализу (для специальности ЭВМ) надо изучить разделы, посвященные пределам функции одной переменной и ее производной.

Пределом функции при называется число «а» такое, что для любого можно найти такое число , что для любого «x» из промежутка будет выполняться неравенство . Имеют место следующие свойства пределов: при , имеющие место и при :



если существуют и не бесконечны , то



и следующие замечательные пределы



Решим задачи, подобные задачам из контрольной работы:

Пример 1. Найти предел L=

Решение: Имеем неопределённость вида .

Если к такой неопределённости сводится предел отношения двух многочленов, при следует в числителе и в знаменателе дроби вынести за скобки самую высокую входящую в них степень аргумента, а затем сократить дробь. Вынесем за скобки в числителе и знаменателе старшую степень аргумента



Так как и при , то предел числителя при

равен 3. Предел знаменателя равен 0. Следовательно, предел

дроби равен .


Ответ: L=