Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материала

Рабочая учебная программа

Содержание 7. Методические указания для студентов 2. Самостоятельная работа Задание №1. Плоскость и прямая в пространстве. Задание №2 Задание №3

Подобный материал:

• Рабочая программа, методические указания по выполнению курсовой работы и контрольные, 1000.11kb.
• Программа и контрольные задания по учебной дисциплине, 858.36kb.
• Программа и контрольные задания по учебной дисциплине «эконометрика» для студентов, 555.04kb.
• Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
• Программа и контрольные задания по учебной дисциплине «трудовое право» для студентов, 805.51kb.
• Программа и контрольные задания по учебной дисциплине «отечественная культура» для, 729.22kb.
• Рабочая программа По дисциплине «Стратегическое управление организацией» Для курса, 197.74kb.
• Программа и контрольные задания по учебной дисциплине «отечественная история» для студентов, 583.38kb.
• Программа, контрольные задания и тематика курсовых работ по учебной дисциплине основы, 557.3kb.
• Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.

7. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ

1. ОБЩИЕ УКАЗАНИЯ

Успешное освоение дисциплины предполагает активное, творческое участие студента путем планомерной, повседневной работы.

Изучение дисциплины следует начинать с проработки рабочей программы, особое внимание, уделяя целям и задачам, структуре и содержанию курса.

2. САМОСТОЯТЕЛЬНАЯ РАБОТА

Самостоятельная работа студентов заключается в изучении рекомендуемой литературы согласно разделам рабочей программы, решении типовых задач, выполнении контрольного задания.

Задачи и упражнения для аудиторной и самостоятельной работы студента обеспечивают закрепление лекционного материала и подготовку к выполнению контрольных работ.

Степень усвоения студентами теоретических знаний и практических навыков проверяется защитой контрольной и лабораторных работ и сдачей зачета по курсу.

ЗАДАНИЕ №1.

Для решения контрольной работы №1 по математике и следует изучить разделы векторной алгебры, линейной алгебры и аналитической геометрии любых учебников. Для решения задач первой контрольной понадобятся следующие понятия и факты:

Для решения первой задачи:

Определители 2 и 3 порядков

-определитель 2-го порядка

Заметим, что у элемента определителя -номер строки, а -номер столбца

- определитель 3 порядка

Векторы и действия над ними.

В декартовой прямоугольной системе координат вектор (или ) имеющий начало в точке А(3,4,0) и конец в точке В(5,7,5) имеет следующие координаты (5-3; 7-4;5-0) или (2,3,5)

Векторы можно складывать и если =+, где (2,3,5) а (4,5,6) то (2+4;3+5;5+6) = (6,8,11)

Можно умножить вектор на число, например если (2,3,5) умножить на (-2) получим вектор -2(-4,-6,-10)

Длина (модуль) вектора обозначается и считается по формуле = для (2,3,5) ||=

Итак, мы имеем заданную в пространстве декартову прямоугольную систему координат ,, - единичные векторы (орты) положительных направлений осей И когда мы пишем, что (2,3,5) это означает, что =

Тройку векторов называют ортонормированным координатным базисом.

2,3,5 - координаты вектора , а

2, 3, 5- компоненты вектора .

Пусть имеем два вектора (2,3,5) и (6,8,11).

Скалярным произведением вектора на вектор называется число (,) = , где угол между и .

В координатной форме

(,) = - т.е. сумме произведений одноимённых координат

=

Скалярное произведение можно использовать, чтобы найти длину вектора.

Скалярный квадрат =

таким образом ==

С помощью скалярного произведения можно найти угол между двумя векторами = , значит

=

Векторным произведением на называется вектор, обозначаемый или и такой, что:

1) длина |[a, b]| = |a|·|b|·sin –т.е. численно равно площади параллелограмма, построенного на векторах и

2) перпендикулярен плоскости векторов и

3) вектора , , и составляют правую тройку, т.е. расположены как большой, указательный и средний палец правой руки.

Координатная форма векторного произведения



или (-7,8,-2)

Смешанное произведение трех векторов , и обозначается и равно , то есть векторной произведение на скалярно умножено на (значит, это число- скаляр)

Численно модуль смешанного произведения равен объему параллелепипеда, построенного на векторах , и .

Координатная форма смешанного произведения



Поскольку в случае компланарности векторов объем соответствующего параллелепипеда равен нулю, то условием компланарности является равенство нулю их смешанного произведения

Плоскость и прямая в пространстве.

Рассмотрим произвольную плоскость и на ней вектор-нормаль , то есть вектор, перпендикулярный плоскости и фиксированную точку .Возьмем текущую точку ,координаты которой меняются так, что точка остается в плоскости, таким образом вектор также всегда, при любых движениях точки лежит в плоскости.

Итак, вектор лежит в плоскости, а вектор ей перпендикулярен. Тогда их скалярное произведение равно нулю:

, или , где

Это общее уравнение плоскости.

Если , то разделив все члены уравнения на получим уравнение плоскости в отрезках



.

абсцисса, ордината и аппликата точек пересечения плоскости с осями

Рассмотрим три заданные точки в пространстве , и .

Как известно, три точки определяют плоскость. Введём текущую точку , координаты которой меняются, но она не выходит за рамки плоскости. Рассмотри три вектора Все они лежат в плоскости , то есть они компланарны и их смешанное произведение равно нулю.



Это уравнение плоскости, проходящей через три заданные точки.

Рассмотрим в пространстве прямую. Её можно задать, задав фиксированную точку, через которую она проходит и задав её направление при помощи вектора.

Итак, напишем уравнение прямой, проходящей через заданную точку и параллельной направляющему вектору . Опять возьмем текущую точку на прямой, т.е. точку, координаты которой меняются так, чтобы она не вышла за пределы этой прямой . Вектор лежит на прямой и, значит, коллинеарен вектору .

Если вектора коллинеарны, то их координаты пропорциональны.

- это и есть канонические уравнения прямой в пространстве.

Обозначим отношение

за



Это параметрические уравнения прямой.

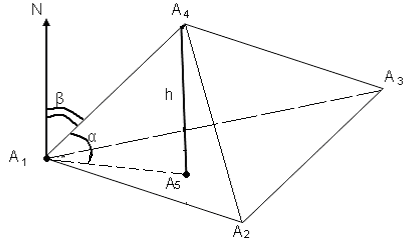
Пример 1. Задана пирамида с вершинами ,,,.



Зная координаты начала и конца вектора , мы можем найти его координаты:

или

Аналогично найдем



1. Теперь найдем угол между ребром и гранью .

Вообще говоря, найти угол между прямой и плоскостью, а угол как раз и является углом между прямой и плоскостью ,- это угол между прямой и её проекцией на плоскость- задача непростая. Угол найти проще, а ведь в сумме они составляют .

Значит, найдя , найдем и =-.

Итак, ищем : это угол между вектором-нормалью к плоскости и вектором .

Отыщем сначала . Какой вектор мы можем выбрать в качестве перпендикуляра к плоскости ? Векторное произведение любых двух векторов, лежащих в плоскости, перпендикулярно плоскости. Возьмем векторное произведение .

==

=

Нас интересует угол между =и .

Скалярное произведение

следовательно



Если , то



- угол между ребром пирамиды и гранью.

2. Найдем площадь грани .

Площадь грани- это площадь треугольника и половина площади параллелограмма, построенного на векторах и .



Но мы знаем из определения векторного произведения, что длина вектора = численно равна площади этого параллелограмма. Длину вектора мы считали в пункте 1 и она равна .

Итак площадь грани =

3. Найдем объем пирамиды;

Объем пирамиды равен =

Если отбросить коэффициент , то получим =-объем призмы, в основании которой лежит , т.е. объем пирамиды равен объема призмы.

А объем параллелепипеда, основанием которого является параллелограмм в 2 раза больше объема призмы следовательно, объём пирамиды - это объема параллелепипеда.

Но объем данного параллелепипеда численно равен модулю смешанного произведения векторов, на которых построен параллелепипед



4. Найдем уравнения прямой - это уравнения прямой, проходящей через заданную точку в направлении , заданном вектором . Итак, пишем уравнение прямой, проходящей через точку А₁ (1,2,3) в направлении вектора



5. Уравнение плоскости :

У нас имеется три точки, лежащие в интересующей нас плоскости, значит используем уравнение плоскости, проходящей через 3 точки:



или



Раскладываем определитель по первой строке







6. Находим уравнения высоты, опущенной из вершины на грань .

Раз эта прямая-высота – она перпендикулярна плоскости , значит в качестве направляющего вектора прямой можно взять вектор , перпендикулярный .

Высота опущена из вершины - значит искомая прямая проходит через точку .

Итак, пишем уравнения прямой, проходящей через заданную точку(3,4,8) в направлении заданного вектора (-6,2,6).



или



Наконец, найдем координаты точки пересечения высоты с нижней гранью.

То есть точку пересечения прямой и плоскости

Перейдем к параметрическому виду уравнений прямой:





и подставим и в уравнение плоскости:









Итак, высота пирамиды пересекается с нижней гранью в точке .

ЗАДАНИЕ №2

Для решения второй задачи потребуются следующие понятия и формулы:

Аналогично тому , как мы действовали в трехмерном случае( в пространстве) при решении первой задачи, рассмотрим на плоскости прямую. Чтобы задать прямую, нужно задать точку, через которую она проходит и вектор, задающий направление: и.







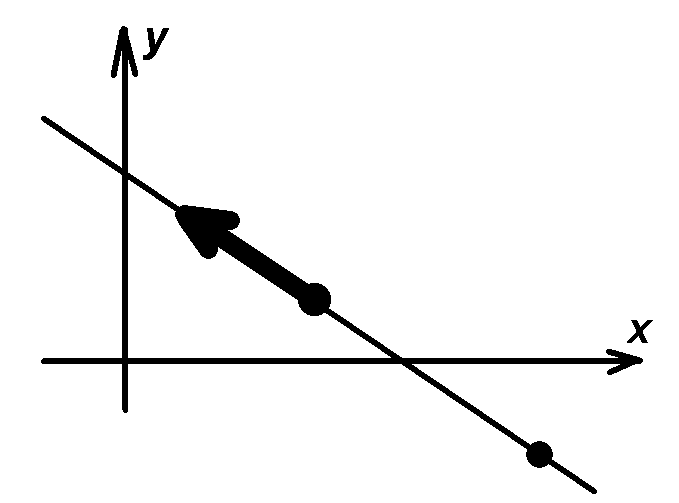
M₀ (x₀, y₀)


M(x, y)


Возьмем текущую точку прямой и рассмотрим вектор .

Вектор коллинеарен вектору и их координаты пропорциональны

- это условие и задает уравнение прямой, проходящей через заданную точку в заданном направлении.

Перенесем все в левую часть и, обозначив числовые коэффициенты другими буквами, получим общее уравнение прямой



Взяв в качестве вектора вектор, соединяющий две точки прямой и ,получим уравнение прямой, проходящей через две заданные точки

.

Выразив и обозначив коэффициент при буквой , а остальные слагаемые буквой , получим уравнение с угловым коэффициентом



Условие параллельности двух прямых

Условие перпендикулярности двух прямых

Если есть отрезок , где и и точка делит его в заданном отношении , то есть

, то

координаты точки

; (формулы деления отрезка в заданном отношении)

Расстояние между точками и вычисляется по формуле, полностью аналогичной формуле расстояния в пространстве, только относительно двух переменных



Пример 1. Задан отрезок , где (-2,5), (4,17).

Определить координаты точки , расстояние от которой до точки в два раза больше, чем расстояние до точки.

По условию задачи

Координаты точки нам неизвестны, но она делит отрезок в отношении .

Итак , =2






Искомая точка имеет координаты

Пример 2. Прямые и являются сторонами треугольника, а точка -точкой пересечения третьей стороны с высотой, опущенной на неё. Составить уравнение третьей стороны.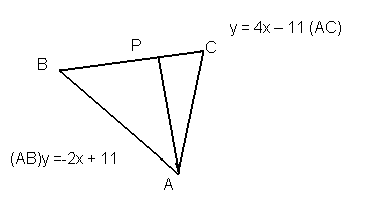



а) Точка А является точкой пересечения прямых АВ и АС, т.е. лежит и на той и на другой прямой. Значит её координаты должны удовлетворять и уравнению прямой АВ и уравнению прямой АС.

сложим уравнения

Итак, точка А (2,-3).

Высота АР – это прямая, проходящая через две заданные точки А и Р:



;

(АР)

то есть угловой коэффициент высоты АР равен -5

в) Прямая ВС перпендикулярна АР, значит её угловой коэффициент

.

Значит её уравнение с угловым коэффициентом имеет вид

(ВС) , где неизвестно.

Но мы знаем, что прямая ВС проходит через точку Р, -значит координаты точки Р обращают уравнение ВС в тождество.

Подставим координаты точки Р в уравнение ВС:


Итак, уравнение ВС:

или

ЗАДАНИЕ №3

Для решения третьей задачи потребуются следующие понятия о кривых второго порядка: Пусть на плоскости имеется прямоугольная декартова система координат. Как было видно в предыдущей задаче, множество точек плоскости, удовлетворяющих равенству =0 является линией.

В примере №2 уравнения были линейными( т.е.функция являлась многочленом первой степени), линия- прямой линией; то есть линиями первого порядка являлись прямые линии. В качестве функции может выступать и многочлен второй степени



такое уравнение – уравнение линии второго порядка.

ЭЛЛИПС

Если уравнение имеет вид



то кривая называется эллипсом (каноническое уравнение эллипса). Точка -центр эллипса. Точки (±,0),(0, ±) называются вершинами эллипса.

(<) – расстояние от центра до фокусов

Если ==0, то центр эллипса совпадает с началом координат и точки (-,0) и (,0) –левый и правый фокусы эллипса.

Число называется эксцентриситетом эллипса.