Geum.ru

Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материалаРабочая учебная программа

Содержание


Задание №16
F(x) – первообразная для f(x).
Задание №17
Подобный материал:
1   ...   6   7   8   9   10   11   12   13   ...   36
Пример 2. Найти интеграл:

Решение : Используем метод интегрирования по частям, основанный на следующем свойстве интегралов:



Очевидно, что применять эту формулу имеет смысл только в том случае, если интеграл в правой части проще, чем в левой, например:
    1. Если подынтегральное выражение слева содержит сомножитель

arcsin x, arcos x, arctg x, ln x

то в качестве u(x) выбирают эти функции.
    1. Если подынтегральная функция имеет вид

,

где- многочлен степени “n”.

Тогда в качестве u(x) берут P(x) и интегрируют по частям n раз. В нашем примере подынтегральное выражение имеет вид

,

Где - многочлен первой степени х.

Итак, мы должны взять







При промежуточном интегрировании постоянную С опускаем.



Затем отыскиваем интеграл в правой части при

и



По интегрированию по частям получаем:

.

Замена переменной под знаком интеграла.

Пример 3. Найти: А) ;

Б) .

Решение: Воспользуемся методом замены переменной. Если



Здесь мы заменили переменную х выражением через t, а dx на.

а) Найдем . Для этого обозначим через t, тогда



Видим что выражение справа – это часть подынтегрального выражения, то есть



Это пример основан на выделении дифференциала новой переменной. Такой вариант метода замены переменной называют «подведением» под знак дифференциала, то есть при



подынтегральная функция является функцией промежуточной переменной умноженной на дифференциал этой переменной:



Иногда удобнее действовать иначе. В случае:

б) имеем иррациональную подынтегральную функцию. Чтобы избавиться от этой иррациональности, воспользуемся основным тригонометрическим тождеством. Для того, чтобы перейти к тригонометрическому виду сделаем замену переменной. Положим

.

Стало быть

.

Тогда

.

Для того чтобы избавиться от степени тригонометрической функции, перейдем к двойному углу.

Имеем



Перейдем обратно к переменной х




Интегрирование рациональной функции.

Пример 4. Найти: А) , Б)

Решение: Как в примере А), так и в примере Б) подынтегральная функция является рациональной дробью, то есть дробью вида

,

где P и Q многочлены степени соответственно m и n.

А) Степени числителя и знаменателя совпадают и равны 3. В этом случае, поделив числитель на знаменатель как многочлен на многочлен, получим сумму многочлена и остатка деления – правильной рациональной дроби. Интегрирование многочленов не сложно, а правильная рациональная дробь раскладывается на сумму дробей стандартного вида – так называемых «простейших» дробей, то есть дробей вида

.

Интегралы от этих дробей известны. Итак, разделим числитель подынтегрального выражения на знаменатель как многочлен на многочлен.





Таким образом, в результате деления мы получим частное, равное 1 и остаток равный (-х + 4). Итак, неправильную дробь можно разложить следующим образом

, то есть

в виде суммы многочлена нулевой степени и правильной дроби. Теперь правильную дробь надо разложить на простейшие. У нас знаменатель уже разложен на множители



Так бывает не всегда. Если это не так, его надо разложить на множители и в соответствии с ними разложить вашу правильную дробь на сумму простейших дробей методом неопределенных коэффициентов:



Приведя к общему знаменателю, получаем:



Два многочлена равны, если равны коэффициенты при соответствующих степенях неизвестного. Приравнивая коэффициенты при одинаковых степенях многочлена в левой части и многочлена в правой, получим:





Приравняв коэффициенты при



Решив совместно эти уравнения, получим

А = 4, В = -4, С = -1

Итак , а

Следовательно,



Заметим, что если- действительный корень знаменателя кратности k, то в разложении ему будут соответствовать k простейших дробей вида . В нашем примере многочлен, стоявший в знаменателе рациональной дроби, имеет один действительный корень = 0 кратности единица – следовательно, в разложении рациональной дроби на сумму простейших этому корню соответствует одно слагаемое.

Если знаменатель имеет комплексные корни, то только попарно сопряженные, так как коэффициенты знаменателя вещественны. Пусть знаменатель кратности имеет комплексно сопряженные корни кратности . Тогда в разложении на простейшие дроби им будут соответствовать простейших дробей вида

,

где

В нашем примере такие комплексные корни имел двучлен . Действительно, приравняв его к нулю, получим <0 – а это означает, что действительных корней нет, комплексно сопряжённые корни кратности 1.

Б) Найдем . Не всегда следует стремиться сразу, определить правильность дроби и разлагать ее на простейшие. В этом задании рациональную дробь можно проинтегрировать без привлечения этого метода.

Подынтегральное выражение равно . Конечно, можно воспользоваться тем, что это неправильная рациональная дробь и проинтегрировать ее, разлагая на сумму многочлена и простейших дробей. Однако, если сделать замену переменой , получим:



В каждом примере на интегрирование результат можно проверить. Достаточно продифференцировать ответ. Если интегрирование было верно, то получится подынтегральное выражение.



Мы получили подынтегральную функцию.

Пример 5. Найти интегралы: А)

Б)

В)

Решение: В данном примере найти требуется интегралы от тригонометрических функций. Интегралы вида

,

где R – рациональная функция от и сводятся к интегралу от рациональной функции относительно новой переменной интегрирования с помощью универсальной тригонометрической подстановки , тогда

В случае А) универсальная тригонометрическая подстановка дает



Но часто универсальная подстановка приводит к громоздким выкладкам, поэтому, где удается, применяют другие подстановки








Случай Б) как раз относится к третьему типу, а именно подынтегральная функция четна как относительно , так и относительно . Положив получим и и заменив по известной тригонометрической формуле



Случай В) относится к первому типу, а именно подынтегральная функция нечетна относительно синуса. Положив и заменив на , получим



ЗАДАНИЕ №16

Следующая задача посвящена вычислению определённого интеграла, например:

Пример 1. Вычислить определенный интеграл

Решение: Определенный интеграл от любой непрерывный функции f(x) вычисляется по формуле Ньютона-Лейбница



где F(x) – первообразная для f(x).

Геометрически определенный интеграл представляет собой при площадь криволинейной трапеции, ограниченной кривой y=f(x), осью ox и прямыми x=a и x=b.

Проинтегрируем сначала соответствующий неопределенный интеграл по частям, положив u=x, dv=sin x dx.



И по формуле Ньютона-Лейбница получим:



Пример 2. Найти

Решение: Находя первообразную с помощью замены переменной при вычислении определенного интеграла, не следует забывать, что, изменив переменную, придется изменить и ее пределы интегрирования.

Обозначим , тогда , , но при x=0, t=0, а при x=4, t=2. Следовательно, в новом интеграле, относительно переменной t изменяются пределы интегрирования:



но так как dt=d(t+1)



Пример 3. Найти площадь фигуры, ограниченной линиями:

Площадь фигуры типа для которой , то есть, для правильной в направлении оси фигуры на рисунке находятся по формуле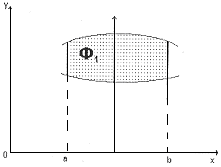










Для фигуры, правильной относительно оси на рисунке, то есть фигуры, которая ограничена



площадь находится по формуле




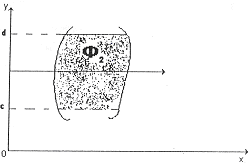
Решение: Решая совместно систему уравнений



найдем абсциссы точек пересечения наших кривых следовательно, пределы интегрирования будут равны a=-1, b=0. Поскольку наша фигура является правильной, как относительно , так и относительно , можно считать ее площадь по первой и по второй формуле. Будем считать по первой.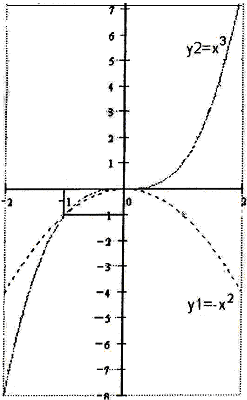



Тогда



ЗАДАНИЕ №17

Далее разберём задачу о вычислении несобственных интегралов.

Определённый интеграл, который рассматривался в предыдущей задаче, вычисляется при двух предположениях:
  1. отрезок интегрирования [a,b] конечен
  2. подынтегральная функция на этом отрезке непрерывна

При таких предположениях интеграл называется собственным интегралом. В том случае, если отрезок интегрирования бесконечен или конечен, но подынтегральная функция на этом отрезке терпит разрыв, интеграл называется