Пояснительная записка 1 Требования к содержанию учебной дисциплины из государственного образовательного стандарта государственный образовательный стандарт высшего профессионального образования

Вид материала

Пояснительная записка

Содержание Требования к выполнению индивидуального задания Индивидуальное задание

Подобный материал:

• Высшего профессионального образования, 345.06kb.
• Пестрякова Людмила Агафъевна, к б. н., доцент Требования государственного стандарта, 67.93kb.
• Ягнышев Борис Сергеевич, Требования стандарта. Государственный образовательный стандарт, 48.94kb.
• Государственный образовательный стандарт среднего профессионального образования государственные, 2099.01kb.
• Государственный образовательный стандарт среднего профессионального образования государственные, 666.88kb.
• Государственный образовательный стандарт среднего профессионального образования государственные, 1374.79kb.
• Пояснительная записка 3 Содержание курса 6 Список литературы 7 III. Рабочая программа, 639.25kb.
• Пояснительная записка 4 Содержание курса 5 Бибилиографический список 6 III. Рабочая, 642.96kb.
• Государственный образовательный стандарт среднего профессионального образования государственные, 743.09kb.
• Государственный образовательный стандарт среднего профессионального образования государственные, 543.84kb.

Требования к выполнению индивидуального задания

При выполнении индивидуального задания необходимо:

1. Переписать задание.
   
2. Представить развернутое решение задания, с обоснованием всех шагов решения.
   
3. При расчете статистических показателей должны быть представлены промежуточные расчеты. Округление производится до сотых.
   
4. Графики должны быть построены с соблюдением масштаба.
   
5. Сделать выводы по полученным расчетам.
   
6. Сдать в сроки установленные преподавателем.
   

Если работа была не зачтена, то необходимо исправить ошибки и сдать работу на повторную проверку.


Индивидуальное задание.


Условие: В фирме проводилось исследование, целью которого, было изучение стажа работы сотрудников фирмы и уровня их заработной платы в у.е. В результате были получены данные приведенные в таблице.

Задание:

1. Произвести выборку объема 30 единиц, начиная с номера соответствующего вашему номеру в журнале.
   
2. Провести структурную и аналитическую группировки. Оформить их в виде соответствующих таблиц. Представить данные структурной группировки в виде круговой диаграммы.
   
3. Построить вариационные ряды, ряды распределения и их графическое представление. Для признака Х построить дискретный ряд распределения. Для признака У – интервальный ряд распределения.
   
4. Рассчитать для каждого из признаков числовые характеристики (среднее значение, дисперсию, среднее квадратическое отклонение, коэффициент вариации).
   
5. По виду графиков выдвинуть гипотезу о виде распределения и проверить ее при уровне значимости α = 0,05.
   
6. Для среднего значения и дисперсии проверить гипотезы о значении данных характеристик для генеральной совокупности (уровень значимости α = 0,05).
   
7. На основе комбинационной таблицы построить корреляционную таблицу для признаков Х и У. Построить корреляционное поле, используя усредненные значения, сделать вывод о виде связи.
   
8. Найти коэффициент ранговой корреляции.
   
9. Считая, что вид связи прямолинейный, вывести уравнение прямой регрессии (любым способом), рассчитать коэффициент корреляции, коэффициент детерминации.
   
10. Для полученных результатов проверить гипотезу о значимости уравнения регрессии и коэффициента корреляции.
    

Таблица данных.

	Стаж	Зар. плата	№	Стаж	Зар. плата	№	Стаж	Зар. плата
	5	34		5	34		5	34
	1	20		1	20		1	20
	2	21		2	21		2	21
	3	22		3	22		3	22
	2	21		2	21		2	21
	4	24		4	24		4	24
	5	28		5	28		5	28
	3	23		3	23		3	23
	3	24		3	24		3	24
	4	29		4	29		4	29
	5	30		5	30		5	30
	3	26		3	26		3	26
	1	20		1	20		1	20
	2	23		2	23		2	23
	3	25		3	25		3	25
	2	21		2	21		2	21
	2	23		2	23		2	23
	5	33		5	33		5	33
	4	28		4	28		4	28
	5	32		5	32		5	32
	3	27		3	27		3	27
	4	30		4	30		4	30
	2	23		2	23		2	23
	1	20		1	20		1	20
	3	24		3	24		3	24
	2	22		2	22		2	22
	5	32		5	32		5	32
	1	20		1	20		1	20
	4	28		4	28		4	28
	2	24		2	24		2	24
	2	23		2	23		2	23
	5	33		5	33		5	33

Глоссарий

№ п.п	Новые понятия	Содержание	Обозначение
1	Высказывание	Повествовательное предложение, о котором можно однозначно сказать истинно оно или ложно	Конкретные высказывания обозначаются начальными заглавными буквами латинского алфавита A, B, C, D, …
2	Сложное высказывание	Строится из простых высказываний при помощи логических связок.	А, В, С, …
3	Логические связки	Логические связки соответствуют операциям над высказываниями и в языке выражаются с помощью союзов и частиц.
4	Отрицание	Новое высказывание, образованное из данного при помощи частицы «не» или слов «неправда, что».
5	Конъюнкция	Новое высказывание, образованное из данных высказываний при помощи союза «и».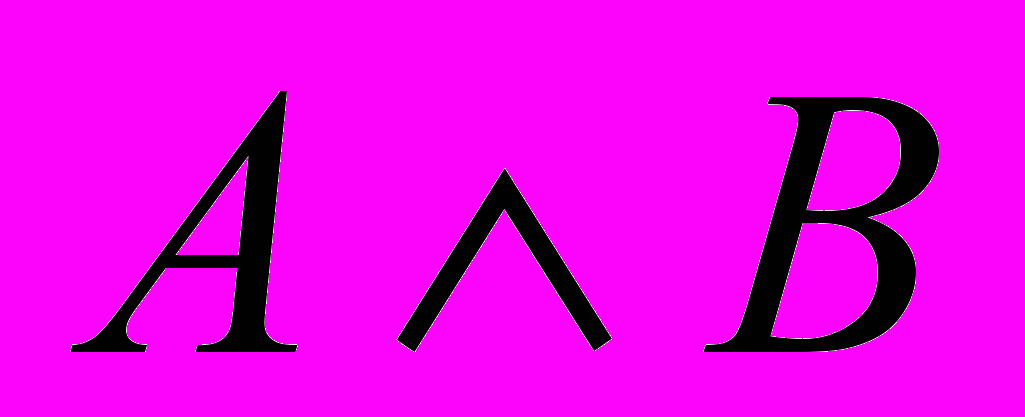
6	Дизъюнкция	Новое высказывание, образованное из данных высказываний при помощи союза «или».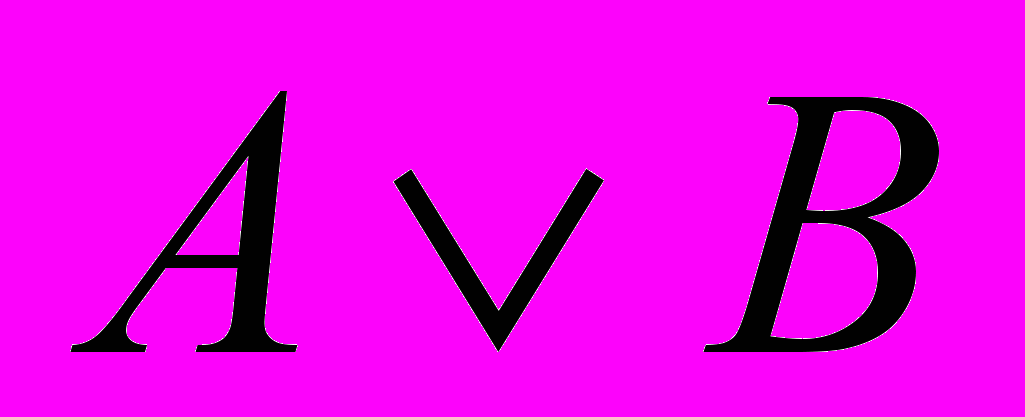
7	Импликация	Новое высказывание, образованное из данных высказываний при помощи слов «если, то».
8	Эквиваленция	Новое высказывание, образованное из данных высказываний при помощи слов «тогда и только тогда, когда».
9	Формула алгебры высказываний	Последовательность букв, обозначающих высказывание, символов логических связок и скобок.	Например:
10	Тавтология	Тождественно истинная формула, которая превращается в истинное высказывание при всякой подстановке вместо переменных конкретных высказываний.	╞
11	Противоречие	Тождественно ложная формула, которая превращается в ложное высказывание при всякой подстановке вместо переменных конкретных высказываний.
12	Равносильные формулы	Формулы называются равносильными, если при любых значениях истинности входящих в них высказываний значения истинности формул совпадают.	≡
13	Предикат	Предикат – неопределенное высказывание, которое содержит переменные, и значение которого зависит от значения входящих в него переменных.	P(x), Q(x), R(x)…
14	Область истинности предиката	Множество значений предикат, при которых он становится истинным высказыванием.
15	Квантор	Специальные слова, при помощи которых из предиката можно образовать высказывание.
16	Квантор всеобщности	Слова: всякий, любой, каждый, никакой и т.д.
17	Квантор существования	Слова: некоторый, есть, хотя бы один и т.д.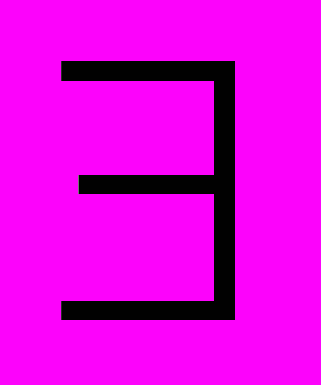
18	Множество	Совокупность каких-либо предметов, объектов, которые рассматриваются как единое целое.	А= { }
19	Пустое множество	Множество, не содержащее ни одного элемента, называется пустым.	Ø
20	Равные множества	Множества называются равными, если они состоят из одних и тех же элементов.	А=В
21	Операция включение множества (подмножество)	Множество А называется собственным подмножеством множества В (включено в множество В), если каждый элемент множества А является элементом множества В. При этом множество А не является ни пустым множеством, ни множеством В.
22	Операция объединение множеств	Множество С называется пересечением данных множеств, если оно состоит их элементов принадлежащих у из данных множеств.
23	Операция пересечение множеств	Множество С называется объединением данных множеств, если оно состоит их элементов принадлежащих хотя бы одному из данных множеств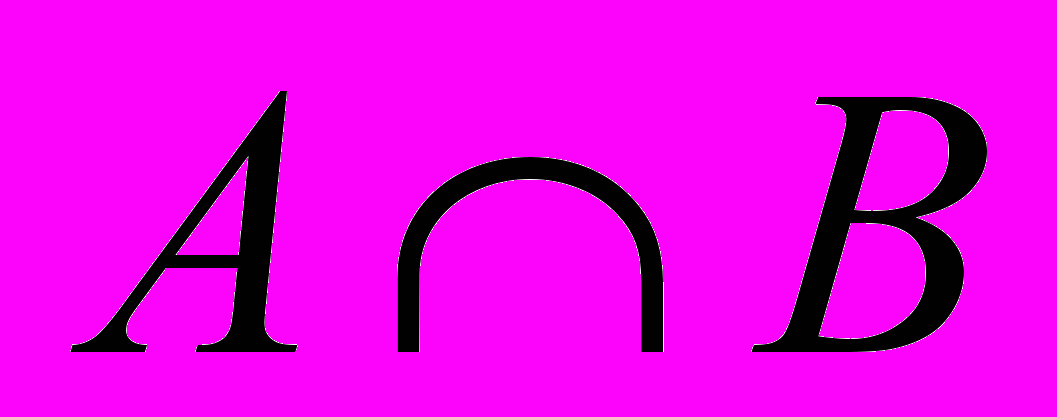
24	Операция разность множеств	Множество С называется разностью множеств, если оно состоит из элементов принадлежащих только одному из данных множеств.
25	Универсальное множество	Множество называется универсальным, если всякое другое множество является его подмножеством	U
26	Операция дополнение множеств	Множество называется дополнением до универсального множества, если оно состоит из элементов принадлежащих универсальному множеству, но не принадлежащих данному множеству.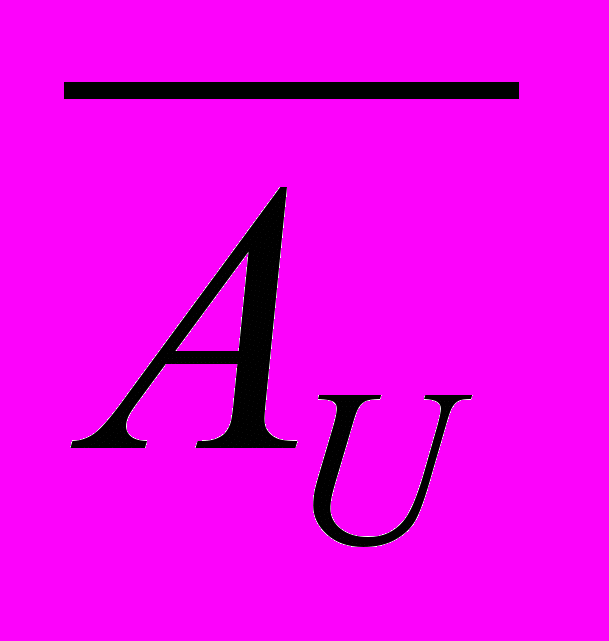
27	Операция декартовое произведение множеств	Множество называется декартовым произведением двух данных множеств А и В, если оно состоит из всевозможных пар вида (x, y), где х – элемент множества А, у- элемент множества В.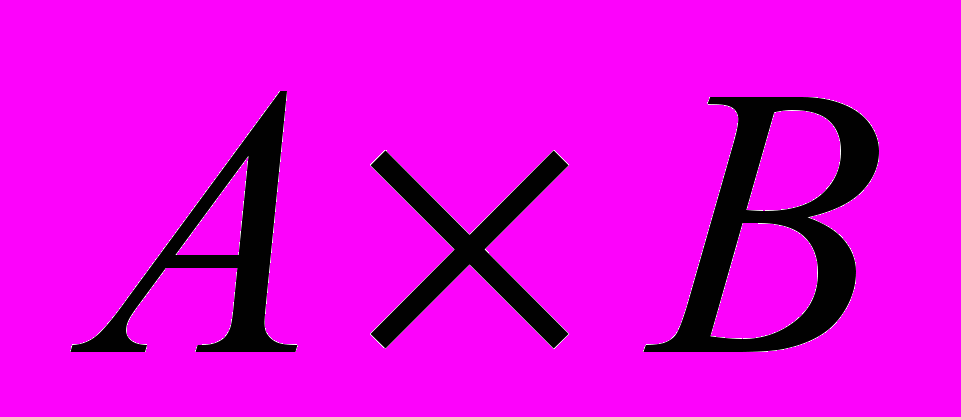
28	Бинарное отношение между множествами	Бинарным отношением (соответствием) между множествами называется любое подмножество декартова произведения данных множеств.
29	Бинарное отношение между элементами данного множества	Бинарным отношением на множестве А называется всякое непустое подмножество декартова квадрата данного множества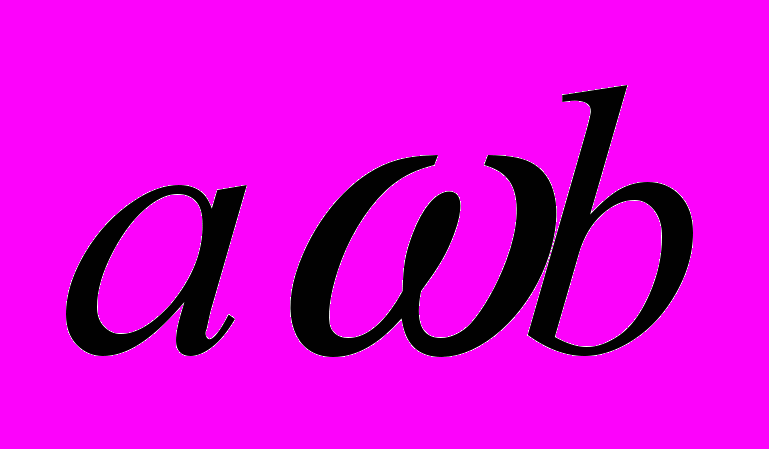
30	Отображение (функция)	Бинарное отношение f между X и Y называется отображением (функцией) из множества Х в множество У, если для всякого элемента из Х существует единственный элемент из У такой, что пара (х,у) принадлежит f.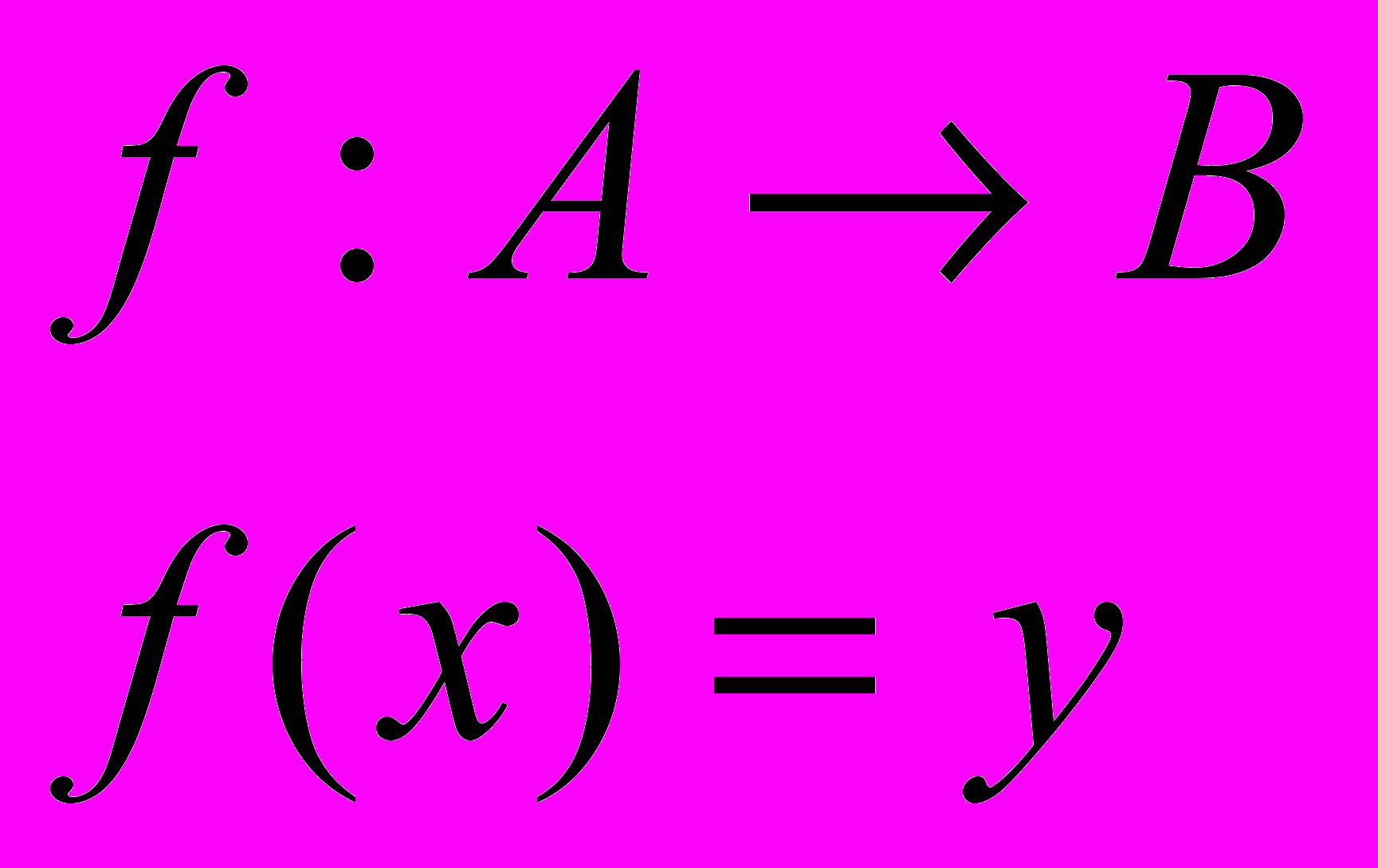
31	Инъективное отображение	Отображение называется инъективным, если всякие два различные элемента из множества Х отображаются в различные элементы множества У.
32	Сюръективное отображение	Отображение называется сюръективным, если каждый элемент из множества У имеет пи этом отображении непустой прообраз.
33	Биективное отображение	Отображение называется биективным, если оно инъективное и сюръективное.
34	Матрица	Система чисел, расположенных в прямоугольной таблице из m строк и n столбцов.
35	Определитель	Число, соответствующее квадратной матрице и находящееся по определенному правилу.
36	Метод Крамера	Метод решения системы линейных уравнений при помощи определителей
37	Метод Гаусса	Метод решения системы линейных уравнений при помощи последовательного исключения переменных.

№ п.п	Новые понятия	Содержание	Обозначение
1	Комбинаторная задача	Задача, в которой необходимо найти количество комбинаций удовлетворяющих тем или иным условиям.
2	Правило произведения	Пусть первый объект можно выбрать m числом способов, второй объект n числом способов, тогда пару объектов можно выбрать mn числом способов
3	Случайный (стохастический) эксперимент	Эксперимент, результаты которого известны теоретически, но не известно какой из них наступит в следующий момент времени
4	Событие	Результат стохастического эксперимента
5	Достоверное событие	Событие, которое наступит всегда в ходе стохастического эксперимента	Ω
6	Невозможное событие	Событие, которое никогда не наступит в ходе стохастического эксперимента	Ø
7	Случайное событие	Событие, которое может произойти, а может не произойти в ходе стохастического эксперимента	А, В, С,….
8	Элементарное событие	Множество, соответствующее данному событию, содержит один элемент
9	Пространство элементарных событий	Множество всех элементарных событий, а также множество всех исходов данного стохастического эксперимента	Ω
10	Сумма событий	Событие, которое происходит в том случае, когда наступает хотя бы одно из данных событий	А+В
11	Произведение событий	Событие, которое наступает в том случае, когда происходят оба события одновременно	АВ
12	Разность событий	Событие, которое наступает в том случае, когда происходит только одно из данных событий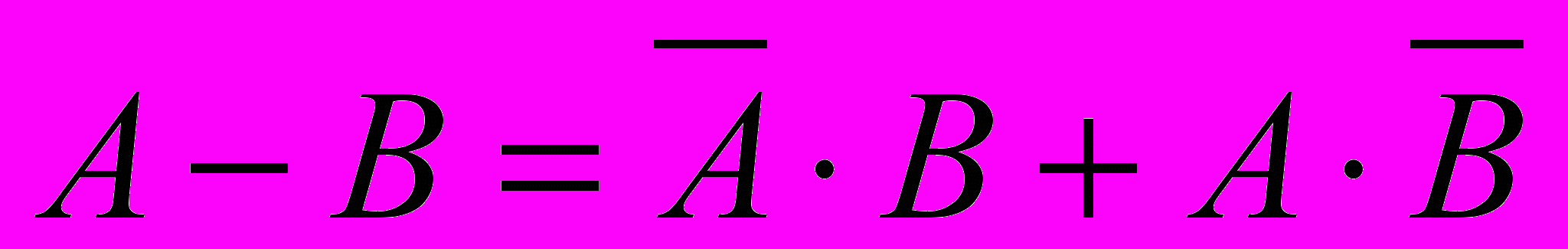
13	Противоположные события	Появление одного события исключает появление другого события
14	Совместные события	События, которые могут произойти одновременно в ходе стохастического эксперимента
15	Несовместные события	События, которые не могут произойти одновременно в ходе стохастического эксперимента
16	Зависимые события	Наступление (не наступление) одного из событий влияет на вероятность наступления (не наступления) другого события
17	Независимые события	Наступление (не наступление) одного из событий не влияет на вероятность наступления (не наступления) другого события
18	Вероятность	Количественная оценка возможности наступления данного события в ходе стохастического эксперимента	р, р(А)
19	Испытание Бернулли	Стохастический эксперимент, который имеет два исхода. Один из исходов – успех, другой – неуспех.
20	Случайная величина	Множество всевозможных исходов стохастического эксперимента, каждый из которых можно выразить числом.	X, Y, Z…..
21	Дискретная случайная величина	Множество исходов стохастического эксперимента, соответствующее данному случайному событию, является конечным
22	Непрерывная случайная величина	Множество исходов стохастического эксперимента, соответствующее данному случайному событию, является бесконечным.
23	Закон распределения	Функция, которая каждому значению случайной величины ставит в соответствие вероятность его наступления.
24	Функция распределения	Вероятность того, что случайная величина Х примет значение меньшее данного действительного числа х.	F (x)=P(X
25	Математическое ожидание	Числовая характеристика случайной величины, характеризующая ее возможное среднее значение.	M(x)
26	Дисперсия	Числовая характеристика случайной величины, характеризующая отклонение ее значений от математического ожидания.	D(x)
27	Среднее квадратическое отклонение	Числовая характеристика случайной величины, характеризующая отклонение ее значений от математического ожидания. Корень квадратный из дисперсии.	σ(х)
28	Правило трех сигм	Практически все значения случайной величины находятся в промежутке .