1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
| § 1. О постоянстве скорости света. Опыт Майкельсона-Морли Об абсолютности классического закона преобразования скоростей. Экспериментальные подтверждения постоянства скорости света. Опыт Майкельсона-Морли. | |
 Галактика "Cомбреро” как совокупность источников света, движущихся с различными скоростями. Фото Peter Barthel. European Southers obsevatory | Об абсолютности классического закона преобразования скоростей. Мы установили, что скорость движения частицы является характеристикой ее состояния. Более того, зная абсолютную скорость частицы и относительные скорости движения тел отсчета, принадлежащих различным ИСО, пользуясь законом преобразования скоростей (2.28), можно найти характеристики состояния частиц в этих ИСО. Рассмотрим является ли данное утверждение абсолютным по отношению к выбору систем отсчета и скорости движения частиц? Если нет, то нам придется пересмотреть описание свойств пространства и времени, из которых получено векторное уравнение (2.28). Напомним, что характеристики пространства, времени и движения тесно связаны с выбором СО и достаточно быстрого синхронизирующего сигнала, в качестве которого мы использовали свет (см. тему 1). Рассмотрим движение физического объекта, перемещающегося со скоростью, близкой к скорости синхронизирующего сигнала. В качестве такого объекта выберем свет. Вектора скоростей распространения узкого луча света относительно условно неподвижной (лабораторной) и движущейся ИСО обозначим соответственно c и c'. Попытаемся ответить на ряд принципиальных вопросов.
 |
 Альберт Майкельсон (1852-1931) Американский физик. Лауреат Нобелевской премии [12} | Опыт Майкельсона-Морли. Рассмотрим один из классических физических опытов, независимо проведенных Майкельсоном и Морли в 1881 и 1887 годах. Первоначальная цель опыта состояла в определении орбитальной скорости Земли относительно эфира. Под эфиром понималась некая "абсолютно неподвижная" среда, в которой перемещались все физические объекты. Измерив скорость света относительно Земли и эфира, можно было бы найти абсолютную скорость орбитального движения Земли, воспользовавшись классическим законом преобразования скоростей (2.28). Эту задачу можно сформулировать более широко. Каким образом движение источников света влияет на скорость их распространения в произвольных ИСО? Для успешной реализации такого эксперимента необходимо было найти объект, перемещающийся достаточно быстро по сравнению со скоростью света. Для этих целей Майкельсоном и Морли была выбрана Земля, орбитальная скорость которой равна = 30 км/с (заметим, что линейная скорость точек, расположенных на поверхности Земли, существенно меньше и составляет всего 0.5 км/с).  |
| | Схема опыта Майкельсона-Морли. Для ответа на поставленный выше вопрос Майкельсон использовал физический прибор, называемый интерферометром. Схема опыта приведена на рис. 15.1. В интерферометре световой луч 1 с помощью полупрозрачного зеркала A разбивался на два когерентных взаимно перпендикулярных луча 2 и 3, движущихся со скоростями с2 и с3 относительно интерферометра. Причем направление распространения луча 3 совпадало со скоростью движения Земли относительно эфира V. Через некоторое время эти лучи отражались от непрозрачных зеркал C и B, расположенных на расстояниях L1 и L2 от полупрозрачного зеркала, возвращались к нему, а затем попадали в оптическую систему D, с помощью которой на фотопленке фиксировалась интерференционная картина. На рис. 15.1 изображено движение световых квантов в двух СО - S, связанной с эфиром, и S', связанной с интерферометром. Пунктирными контурами показано положение деталей интерферометра (зеркал A, B и C и приемного устройства D) относительно эфира в моменты, соответствующие отражению лучей 2 и 3 от зеркал (один штрих соответствует моменту отражения луча 2 от зеркала C, а два штриха - повторному попаданию отраженных лучей 2 и 3 на зеркало A). В итоге оба этих луча попадут в приемное устройство D (D''). При проведении расчетов предположим, что регистрация интерференционной картины, создаваемой когерентными лучами 2 и 3, в детекторе происходит мгновенно после выхода лучей из зеркала A''. 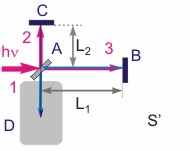 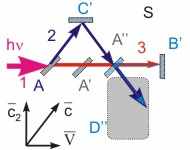 Рис. 15.1. Ход световых лучей в интерферометре в собственной S’ и лабораторной S системах отсчета Дополнительный временной сдвиг в прохождении лучей, который возник бы по сравнению со случаем "неподвижной" Земли, должен был вызвать появление соответствующей геометрической разности хода лучей, а следовательно, и изменение вида интерференционной картины. Остановить движение Земли по орбите в данном эксперименте, конечно не удастся, однако можно развернуть интерферометр на 900 и получить желаемый сдвиг фаз между когерентными лучами 2 и 3 за счет изменения геометрической разности хода этих волн на противоположную по знаку.  |
| | Обсуждение результатов опыта Майкельсона-Морли. Разность времени прохождения лучей 2 и 3 от зеркала А и возвращения их обратно (от A до A'') можно рассчитать, исходя из классического закона преобразования скоростей (2.28). Она окажется равной: t1 = (2/c)·2·(L1 - L2/2) + (L1 - L2)), где L1 и L2 - расстояние между зеркалами AB и AC соответственно в горизонтальном и вертикальном направлениях (см. рис. 15.1); = /c. Аналогично рассчитывается величина временной задержки световых сигналов t2, наблюдаемая при повороте интерферометра на 90 градусов (пространственный отрезок L1 в приведенной выше формуле заменяется на L2). Суммарный временной сдвиг, который должен был бы фиксироваться детектором при повороте интерферометра, составляет величину (L1 + L2)·2/c, что соответствует изменению разности хода лучей на величину x = (L1 + L2)·2. Для использованной в эксперименте установки отношение x = 1/5, что, в принципе, позволяло обнаружить относительный сдвиг интерференционных полос на двух снимках, вызванный этой разностью хода лучей. Результат опыта никакого смещения интерференционных полос не обнаружено, т.е. движение Земли в пределах точности эксперимента не оказывает влияния на скорость распространения света. Впоследствии удалось повысить точность опыта, но результат не изменился. Скорость света в вакууме одинакова во всех инерциальных системах отсчета.  |
| | Экспериментальные подтверждения постоянства скорости света. Кроме опыта Майкельсона - Морли существует большое количество экспериментальных фактов, подтверждающих положение о постоянстве скорости света в различных ИСО вне зависимости от скорости движения источника и приемника света. К таким фактам относятся:
Существует еще целый ряд замечательных экспериментов, подтверждающих постоянство скорости света, а именно:
Результаты этих экспериментов позволяют сделать вывод о том, что скорость света не зависит от выбора СО. Логично предположить, что скорости других физических объектов, моделируемых частицами, при приближении их скоростей к скорости света также будут независимы от выбора СО. с = 2.99792458·108 м/с.  |
§ 2. Постулаты специальной теории относительностиПостоянство скорости света и классические представления о свойствах пространства и времени. Парадокс двух световых сфер. Постулаты специальной теории относительности.  | |
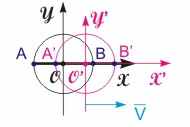 Рис.15.2. Парадокс двух световых сфер | Постоянство скорости света и классические представления о свойствах пространства и времени. Экспериментально установленный факт постоянства скорости света в любых ИСО противоречит классическому закону преобразования скоростей (2.28). Следовательно, классические свойства пространства и времени, из которых получен этот закон, не распространяются на общий случай произвольно движущихся ИСО. Эти свойства в общем случае необходимо пересмотреть. Примером противоречия, возникающего при попытке применения классических свойств пространства и времени к описанию движения быстро движущихся частиц, служит ситуация, названная парадоксом двух световых сфер. Рассмотрим распространение светового сигнала в двух ИСО. Пусть система S' движется относительно S вдоль оси X с постоянной скоростью V (см. рис. 15.2) и в момент времени t = t' = 0 положения тел отсчета совпадали. В этот момент времени из точки O = O' был испущен световой сигнал. Отметим на оси X две точки A и B, отстоящие от тела отсчета на равном расстоянии r = OA = OB. До них сигнал в системе S дойдет за время t = r/c. Аналогично для другой ИСО выберем положение соответствующих точек A' и B' таким образом, чтобы r' = OA' = OB' = r и t' = r'/c. Куда успеет распространиться сигнал через промежуток времени t' = t в этих системах отсчета? С точки зрения наблюдателя, находящегося в системе S, сигнал одновременно дойдет до точек A и B, причем сначала он достигнет точки A', затем A и B и только после этого придет в B'. Наблюдатель, находящийся в системе S', обнаружит, что сигнал в один момент времени будет зафиксирован в точках A' и B' и не одновременно в А и В. Следовательно, одновременность является относительным понятием и определяется выбором ИСО. Противоречие возникает ввиду того, что, приняв факт постоянства скорости света за истину, мы не изменили наши представления о свойствах пространства и времени. Таким образом, для адекватного описания физического мира необходимо пересмотреть пространственно-временные отношения при больших скоростях движения систем.  |
| | Постулаты специальной теории относительности. Проанализировав эти противоречия и другие опытные факты по распространению света, Эйнштейн пришел к выводу, что представления Ньютона о свойствах пространства и времени как об абсолютных категориях, не зависящих от выбора системы отсчета, имеют ограниченную область применимости. Он предложил новую физическую теорию, описывающую движение свободных частиц в произвольных ИСО и адекватно отражающую свойства пространства и времени. Эта система научных положений получила название специальной теории относительности (СТО). СТО базируется на двух постулатах, являющихся обобщением экспериментально установленных фактов.
 |
§ 3. Преобразования ЛоренцаО необходимости пересмотра пространственно-временных отношений. Использование принципа симметрии для установления связи между пространственными и временными координатами в различных ИСО. Прямые и обратные преобразования Лоренца.  | |
 Альберт Эйнштейн (1879-1955). Немецкий физик-теоретик. Лауреат Нобелевской премии | О необходимости пересмотра пространственно-временных отношений. Поскольку представления Ньютона о свойствах пространства и времени не распространяются на случай движения с большими скоростями, то преобразования Галилея, из которых они вытекают, также имеют ограниченную область применимости. Актуальной становится задача о нахождении таких преобразований координат и времени, которые, совпадая с преобразованиями Галилея при малых скоростях, объясняли бы указанные выше экспериментальные факты и противоречия для релятивистского случая (случая больших скоростей). Итак, требуется найти связь между пространственными и временными координатами в ИСО, движущихся относительно друг друга с произвольной постоянной скоростью. Пусть система S' движется относительно системы S вдоль оси X с постоянной скоростью V. При этом выполняется ряд условий:
 |
| | Использование принципа симметрии для установления связи между пространственными и временными координатами в различных ИСО. Так как движение системы S' происходит вдоль оси X, то очевидно, что при переходе от одной СО к другой проекции на оси OY и OZ не изменяются y = y', z = z'. Связь между величинами x и x' будем искать, исходя из принципа симметрии. Искомая связь x' = f'(x, t) должна быть линейной, поскольку в соответствии с принципом симметрии пространство и время однородны. Напомним, что однородность проявляется в том, что величины пространственного и временного интервалов не зависят от положения тела в пространстве и абсолютного значения времени t. Следовательно, величина приращения координаты x' не должна зависеть от значений x и t. Найдем полный дифференциал величины x'. Исходя из его определения, имеем, что: 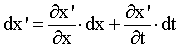 , (15.1) , (15.1)где ∂x'x = ∂x и ∂x't = ∂t - частные производные от искомой функции f'(x, t) по координате и времени; dx' - полный дифференциал функции f'(x, t). Из курса математического анализа известно, что полный дифференциал функции f'(x, t) приблизительно равен приращению этой функции df' = f' при малых приращениях аргументов x и t. Исходя из вышеизложенного, приращение x', а следовательно, и частные производные функции x' = f(x, t) не должны зависеть от x и t. Таким образом, величина x' должна быть линейной функцией этих переменных. Кроме того, наличие линейной связи обеспечивает установление однозначного соответствия между пространственными координатами при переходе от одной системы отсчета к другой (квадратное уравнение, например, имеет два решения, что ведет к неоднозначности трактовки результата преобразований). Соотношение между координатами будем искать в виде: x' = ·(x - V·t); (15.2) x = ·(x' + V·t'), (15.3) где - константа, не зависящая от x и t. В уравнении (15.3) мы, учитывая обсужденный ранее парадокс двух световых сфер, заранее допустили, что время течет по-разному в различных ИСО. Вопрос о конкретном соотношении величин t и t' пока оставим открытым.  |
 Хенрих Лоренц (1853-1928). Нидерландский физик. Лауреат Нобелевской премии | Преобразования Лоренца. Учитывая постулат о постоянстве скорости света, найдем расстояние, на которое распространится сигнал за время t в разных ИСО. x = c·t; (15.4) x' = c·t'. (15.5) Подставим уравнения (15.4) и (15.5) соответственно в (15.2) и (15.3): c·t' = ·(c - V)·t; (15.6) c·t = ·(c + V)·t'. (15.7) Перемножив уравнения (15.6) и (15.7), найдем коэффициент : 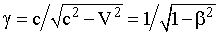 . (15.8) . (15.8) Из уравнения (15.8) видно, что при малых скоростях этот коэффициент равен единице, а преобразования координат (15.2) и (15.3) совпадают с преобразованиями Галилея. По мере приближения скорости системы к скорости света величинастремится к бесконечности. Итак, формулы преобразования координат при переходе от одной ИСО к другой, движущейся относительно нее со скоростью V вдоль оси OX, будут иметь вид: 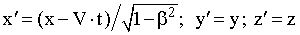 ; (15.9) ; (15.9) 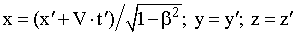 . (15.10) . (15.10) Решив приведенные уравнения относительно времени, получим соответствующие выражения для его преобразования при переходе от одной ИСО к другой: 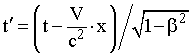 ; (15.11) ; (15.11) 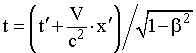 . (15.12) . (15.12) Уравнения (15.9) и (15.11) называются прямыми, а уравнения (15.10) и (15.12) - обратными преобразованиями Лоренца. Соотношения (15.9)-(15.12) впервые получил Лоренц при рассмотрении теории электромагнитных явлений. Эйнштейн трактовал эти соотношения как отражение объективных свойств физического мира, в котором временные и пространственные характеристики непосредственно связаны между собой и зависят от выбора системы отсчета. Преобразования Лоренца отражают единство пространственно-временных отношений, совпадая при малых скоростях с преобразованиями Галилея.  |
§ 4. Кинематические эффекты специальной теории относительностиОтносительность одновременности. Эффект сокращения длины. Эффект замедления времени. Причинно-следственные отношения в релятивистском случае. Предельная скорость распространения физического взаимодействия.  | |
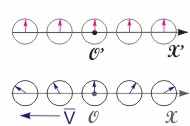 Рис. 15.4. Показания часов в ИСО с точки зрения наблюдателя, находящегося в S’ системе 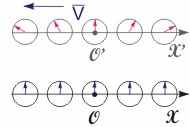 Рис. 15.5. Зависимость показаний часов в движущейся СО при изменении направления ее скорости | Относительность одновременности. Напомним, что два события, происходящие в различных точках пространства одной системы координат, называются одновременными, если они происходят в один момент времени по часам этой системы. Пусть в неподвижной СО S в момент времени t0 произошли события в точках с координатами x1 и x2. В движущейся СО S' эти события произойдут в точках x'1 и x'2 в разные моменты времени t'1 и t'2 по часам этой системы. Исходя из преобразований Лоренца, найдем промежуток времени t' = t'2 - t'1: 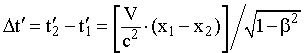 . (15.13) . (15.13)Следовательно, понятие одновременности не является абсолютным. События, одновременные в одной системе координат t', не являются одновременными в другой. Из формулы (15.13) видно, что в случае движения штрихованной системы слева направо в областях пространства x1 > x2 имеет место неравенство t'2 > t'1, а для областей x1 < x2 выполняется противоположное соотношение t'2 < t'1. 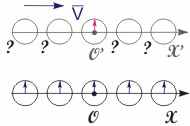 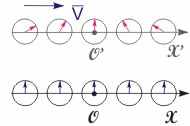 Рис. 15.3. Особенности хода часов в ИСО, движущихся с большими скоростями. Следовательно, показания часов в штрихованной системе координат будут различными в зависимости от места расположения часов. В рассматриваемом примере часы, расположенные слева от исходной точки O, идут быстрее, чем часы, расположенные справа (см. рис. 15.3). С точки зрения наблюдателя, находящегося в S' системе, все ее синхронизированные часы покажут одинаковое время (то есть ti' = t0', где i - порядковый номер часов), а часы S системы в соответствии с преобразованиями (15.12) покажут разное время: 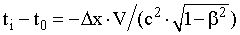 . .В данном случае неподвижной является S' система, а направление скорости, в отличие от показанного на рис. 15.3, меняется на противоположное (проекция скорости движения системы на горизонтальную ось отрицательна: Vx = -V < 0). Следовательно, положение стрелок часов будет выглядеть согласно рис. 15.4. Приведенные результаты полностью соответствуют принципу равноправности ИСО. Действительно, по отношению к условно неподвижной системе S часы, расположенные правее от точки отсчета O' по ходу движения СО S', идут медленнее, а левее - быстрее. Таким образом, нельзя путем выбора ИСО определить, какая из них движется, а какая покоится. В случае изменения направления движения системы S' на противоположное показания часов будут соответствовать рис. 15.5. Из сравнения рис. 15.4. и 15.5 видно, что ход движущихся часов относительно неподвижных полностью идентичен. Важно, что в зависимости от положения часов и направления скорости движущейся системы S' порядок наступления событий в различных точках пространства может измениться. Однако, это утверждение не относится к событиям, находящимся в причинно-следственной связи.  |
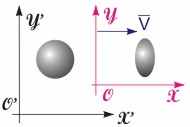 Рис. 15.6. Эффект сокращения длины | Эффект сокращения длины. Рассмотрим две СО, движущиеся друг относительно друга вдоль оси X. Пусть стержень, сориентированный вдоль этой оси, покоится относительно системы S'. Длина стержня в этой системе, называемой собственной системой отсчета (ССО), равна L0, и сам он перемещается слева направо со скоростью V относительно наблюдателя, находящегося в системе S. За длину движущегося стержня L примем разность координат концов стержня, зафиксированную в один момент времени по часам лабораторной СО S, в которой находится наблюдатель, т.е. L = x2 - x1, если t1 = t2. Воспользовавшись преобразованиями Лоренца, найдем связь между длинами стержня в разных СО. 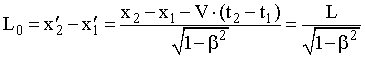 , (15.14) , (15.14)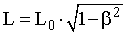 . (15.15) . (15.15) Из формулы (15.15) видно, что:
Если стержень расположить перпендикулярно направлению движения (вдоль осей OY или OZ), то в соответствии с преобразованиями Лоренца (5.9) его длина не изменится. Размеры тел в направлениях, перпендикулярных направлению движения, не изменяются. Неизменность поперечных и изменение продольных размеров приводит к эффекту "сплющивания" тел в системах, движущихся относительно ССО S' (см. рис. 15.6). Трактовать эффект изменения формы объекта будем следующим образом. За форму тела примем положение координат его краев, зафиксированное в один и тот же момент времени. При этом измерение времени будем проводить по часам движущейся системы. Наличие преобразований Лоренца приведет к изменению положения этих координат в лабораторных СО, которые движутся относительно исследуемых объектов. Эффект сокращения длины чисто кинематический. С самим объектом ничего не происходит (шар не подвергается деформации), изменения происходят только с масштабом длины, т.е. пространство искривляется. Эти изменения будут тем больше, чем больше скорость движения ЛСО.  |
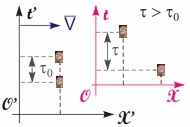 Рис. 15.7. Замедление хода движущихся часов | Эффект замедления времени. Пусть в собственной СО происходит событие длительностью 0. 0 = t'2 - t'1, где t'1 и t'2 - время начала и конца события по часам ССО S'. Точка, в которой происходит событие, покоится относительно S'. В ЛСО S начало и конец события будут происходить в разных точках x1 и x2 в другие моменты времени t1 и t2 (см. рис. 15.7). Исходя из преобразований временных координат (15.11) и (15.12), найдем величину промежутка времени между началом и концом события в системе S: 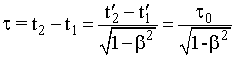 . (15.16) . (15.16)Из формулы (15.16) видно, что:
Время, которое измеряется по часам, движущимся совместно с частицей, называется собственным временем. Пример. Рассмотрим движение элементарной частицы ( - мезона) в лабораторной системе отcчета, связанной с Землей. Длину пути, пройденного этой частицей от рождения до распада на позитрон и два нейтрино, можно определить, измерив скорость - мезона и зная собственное время жизни этой частицы. В отличие от классического случая, для которого L = 0·V, эксперимент показал, что выполняется следующее соотношение, связывающее путь и скорость движения - мезона: 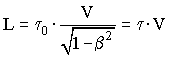 , (5.17) , (5.17)где 0 - собственное время жизни - мезона; - время жизни - мезона в лабораторной СО; V - его скорость в ЛСО, равная относительной скорости движения ССО. Соотношение (15.17) наряду с другими экспериментальными фактами подтверждает вывод о замедлении хода движущихся часов по сравнению с часами, расположенными в ССО, и формулу (15.16).  |
| | Причинно - следственные отношения в релятивистском случае. Предельная скорость распространения физического взаимодействия. Вопрос. Поскольку последовательность одних и тех же событий различна в зависимости от направления скорости движения СО, может ли так случиться, что в одной СО причина предшествует следствию, а в другой, наоборот, следствие предшествует причине? Можно показать, что при условии распространения физического взаимодействия со скоростью, меньшей скорости света, это невозможно. Пусть в двух точках некоторой системы отсчета произошли события, разделенные промежутком времени ∆t > 0. Покажем, что если эти события причинно связаны в данной системе (например, сдвиг заряженной пластины и вызванное им изменение положения заряженного тела в пространстве), то они причинно связаны и в любой другой ИСО. Другими словами докажем, что соответствующий промежуток времени ∆t' в произвольной ИСО будет также положительным. Рассмотрим распространение взаимодействия в двух ИСО S и S'. Пусть система S' движется вдоль оси X со скоростью V. Рассмотрение проведем относительно наблюдателя, покоящегося по отношению к системе S. Для определенности будем считать, что в ИСО S источник воздействия находился в точке с координатой x1 в момент времени t1, а физический объект, на который это воздействие оказано, - в точке x2 в момент t2. Исходя из преобразований Лоренца (15.11), величину ∆t' можно рассчитать по формуле: 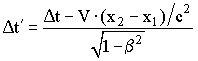 . (5.18) . (5.18)Величину временного интервала t' = t'2 - t'1можно найти, зная скорость распространения физического взаимодействия υ в системе S: t = (x2 - x1)/υ. (15.19) Следовательно, 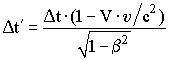 . (15.20) . (15.20)Из формулы (15.20) следует, что величина t' будет положительной (при t > 0), если выполняются следующие неравенства: 1 - V·υ/c2 > 0. (15.21) υ/c < c/V. (15.22) В соответствии с постулатами СТО скорости движения тел, в том числе и тел отсчета, ограничены значением скорости света в вакууме. Действительно, преобразования Лоренца теряют физический смысл, если V > c или V = 0, поскольку в знаменателе выражений (15.9)-(15.12) подкоренное выражение становится отрицательным или равным нулю. Таким образом, не существует ИСО, связанной с частицей, которая движется со скоростью света, и не существует такой ИСО, в которой фотон (световой квант) покоится. Следовательно, минимальное значение правой части выражения (15.22) не превышает единицы и максимальная скорость распространения физического взаимодействия, при которой сохраняются причинно-следственные отношения, меньше скорости света в вакууме υ < с. Причинно-следственные отношения сохраняются, когда скорость распространения взаимодействия не превышает скорость света в вакууме. Таким образом, не существует такой СО, в которой при наличии предельной скорости распространения физического взаимодействия причина и следствие поменялись бы местами. |
