1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 3. Пространство Минковского. 4-вектор расстояния Пространство Минковского как отражение единых пространственно-временных отношений. Мир событий - четырехмерное псевдоевклидово пространство, называемое пространством Минковского. R в четырехмерном пространстве как комбинации проекций: R Примеры 4-скаляров: собственное время, скорость света в вакууме.Примеры Об абсолютном характере физических законов, выраженных через 4-векторы и 4-скаляры. Физические законы, записанные как комбинации 4-векторов и/или 4-скаляров, имеют предпосылки быть абсолютными.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 3. Пространство Минковского. 4-вектор расстояния

Пространство Минковского как отражение единых пространственно-временных отношений.
Особенности пространства Минковского.
Понятие 4-скаляра и 4-вектора.
Об абсолютном характере физических законов, выраженных через 4-векторы и 4-скаляры.

Герман Минковский (1864-1909). Немецкий математик и физик.

Пространство Минковского как отражение единых пространственно-временных отношений. Проведем более детальное сравнение пространственного и пространственно-временного интервалов r и I.  Эти величины инвариантны по отношению к операциям сдвига и поворота осей координат:

	величина r2 инвариантна относительно сдвигов начал координат и поворотов трех пространственных осей OX, OY, OZ (см. тему 1);
	величина I2 инвариантна относительно сдвигов начал отсчета четырех осей OX, OY, OZ, Ot, поворотов в плоскостях XY, XZ, YZ и преобразований Лоренца на плоскостях Xt, Yt, Zt.

Эти преобразования являются линейными и по аналогии с преобразованиями поворота в плоскостях XY, XZ, YZ в трехмерном пространстве (1.4) их можно рассматривать, как своеобразный поворот в четырехмерном пространстве. С этой точки зрения инвариантность интервала I² как комбинация пространственных и временных координат отражает свойства симметрии единого четырехмерного мира событий.

Мир событий - четырехмерное псевдоевклидово пространство, называемое пространством Минковского.

 


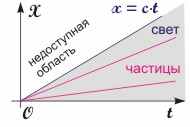
Рис. 16.2. Доступные области пространства Минковского (двумерный случай).

Пространство Минковского отличается от обычного евклидова пространства по двум причинам. Во-первых, не все области пространства Минковского доступны (см. рис. 16.2) поскольку существующие в природе мировые линии могут находиться лишь в области времениподобных интервалов. Во-вторых, величина пространственного интервала может принимать отрицательные значения, т.к. в величину I² входят четыре слагаемых, три из которых отрицательны. Таким образом, пространство Минковского по отношению к евклидову является особенным.

По аналогии с приращением радиус-вектора в евклидовом пространстве введем понятие вектора расстояния  R в четырехмерном пространстве как комбинации проекций:

R = {c·t, x, y, z}.     (16.21)

Вектор R задает положение частицы в пространстве Минковского и имеет компоненты R_t = c·t, R_x = x, R_y = y, R_z = z. Четврехмерный вектор, компоненты которого подчиняются преобразованиям Лоренца, называется 4-вектором (четыревектором). Можно доказать, что квадрат модуля 4-вектора есть инвариант в пространстве Минковского, т.е. является 4-скаляром. Квадрат модуля 4-вектора R равен:

R² = R_t² - R_x² - R_y² -  R_z² = I².     (16.22)

Величину R² называют 4-скаляром. Как мы показали ранее, она является инвариантом по отношению к выбору ИСО.  

Примеры 4-скаляров: собственное время, скорость света в вакууме.
Примеры 4-векторов: пространственно-временной интервал, вектор энергии-импульса P (17.11).

Поскольку мир событий представляет собой пространство Минковского, то существуют ограничения, накладываемые на физические величины, пригодные для объективного описания природы. При переходе от одной ИСО к другой проекции этих величин должны быть связаны соотношениями, аналогичными преобразованиям Лоренца, или их комбинация, аналогичная R², не должна изменяться. Такие величины называются релятивистски ковариантными.



 

Об абсолютном характере физических законов, выраженных через 4-векторы и 4-скаляры. Фундаментальные физические законы должны подчиняться принципу относительности, т.е. не зависеть от выбора ИСО. Данное условие выполняется автоматически, если эти законы записываются через физические величины, являющиеся 4-векторами или 4-скалярами.

Физические законы, записанные как комбинации 4-векторов и/или 4-скаляров, имеют предпосылки быть абсолютными.

Подтверждает это положение тот факт, что 4-вектора можно складывать и умножать на числа по аналогии с правилами, действующими для векторов в евклидовом трехмерном пространстве.

Для наглядности законы физики удобнее представлять в лабораторной системе отсчета (системе, где покоится наблюдатель). Запись в ЛСО обычно сопровождается законами преобразований координат и времени в другие ИСО, например, преобразованиями Лоренца. Законы, согласующиеся с преобразованиями Лоренца, называются релятивистскими.

Альтернативный способ формулировки физических законов - их запись в виде 4-векторов и 4-скаляров. Еще раз отметим, что такая формулировка является более компактной, но менее наглядной.