1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 4. Свойства симметрии и принцип физического подобия О симметрии физических систем и законов. Симметрия физических систем по отношению к масштабным преобразованиям. § 1. Основной закон релятивистской динамики. Закон сохранения импульса R = {c·dt, dx, dy, dz} - 4-вектор расстояния в пространстве Минковского. Поскольку P Физическая величина P, задаваемая выражением (17.11), называется 4-вектором энергии-импульса. Скорость изменения релятивистского импульса системы невзаимодействующих частиц равна векторной сумме всех сил, действующих на не Релятивистский импульс замкнутой системы невзаимодействующих частиц сохраняется.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 4. Свойства симметрии и принцип физического подобия

О симметрии физических систем и законов.
Симметрия физических систем по отношению к масштабным преобразованиям.
Принцип подобия в физике.

 

О симметрии физических систем и законов. Свойства симметрии присущи не только пространству и времени. Они характерны для физических систем в целом и для законов, описывающих соотношения между физическими характеристиками и их изменениями в пространстве и времени.

Свойства симметрии применительно к законам физики обуславливает их инвариантность к определенным преобразованиям, которым могут быть подвергнуты исследуемые системы. Одним из наиболее общих преобразований такого рода является масштабирование, обуславливающее изменение координат и времени в определенное число раз:

r' = A·r;     (16.23)
t' = B·t,     (16.24)
где A и B - положительные константы.

 

 

Симметрия физических систем по отношению к масштабным преобразованиям. Рассмотрим, как в случае масштабирования изменится кинетическая, потенциальная и полная механическая энергии системы. В нерелятивистском случае кинетическая энергия системы, пропорциональная квадрату скорости, после масштабных преобразований в соответствии с (16.23) и (16.24) станет равной:

E_к' = (A/B)²·E_к.     (16.25)

Потенциальная энергия определяется конфигурацией системы и пропорциональна координате в степени n:

E_п'(r) ~ rⁿ,     (16.26)
где n = 1 для однородного поля силы тяжести,
n = - 1 для гравитационного поля,
n = 2 для поля сил упругости.

Следовательно, потенциальная энергия системы после проведения масштабных преобразований окажется равной:

E_п' = Aⁿ·E_п.     (16.27)

Можно доказать, что полная механическая энергия системы будет изменяться по закону, аналогичному (16.27), т. е.

E' = Aⁿ·E     (16.28)

в случае, если

B = A^1-n/2.     (16.29)

Из формулы (16.28) вытекает, что в случае сохранения полной механической энергии в одной из физических систем она также сохраняется в подобной ей системе, подвергнутой масштабным преобразованиям (16.23), (16.24), а изменение энергии будет в этих системах происходить по одним и тем же законам с масштабным коэффициентом Aⁿ. Таким образом, выражение (16.27) является проявлением свойства симметрии к рассматриваемым преобразованиям координат и времени.



 

Принцип подобия в физике. Преобразование энергии (16.28), с одной стороны, можно трактовать как результат изменения масштабных единиц пространства и времени в неизменной физической системе, а с другой - как преобразование энергии при изменении самой физической системы и сохранении масштабов координат и времени (например, изменения расстояний между взаимодействующими телами). Первый и второй варианты приведут к одному и тому же результату с точки зрения выполнения закона преобразования энергии (16.28) в случае выполнения соотношения (16.29).

Последнее утверждение позволяет сформулировать принцип физического подобия.

Изменение линейных размеров системы в A раз
приведет к изменению характерных времен в B раз, где B = A^1-n/2.

Примеры.
1. Движение в гравитационном поле. В данном случае n = - 1 и выполняется соотношение t'/t = (r'/r)^3/2.
Это выражение соответствует 3 закону Кеплера, утверждающему, что квадраты периодов обращения планет пропорциональны кубам их больших полуосей.
2. Гармонические колебания груза на пружине. В данном случае n = 2 и выполняется равенство t'/t = 1. Таким образом, период колебаний груза на пружине не зависит от амплитуды этих колебаний.

Из приведенных примеров следует, что принцип физического подобия позволяет связать пространственные и временные характеристики движения, не прибегая к законам динамики.

§ 1. Основной закон релятивистской динамики. Закон сохранения импульса О применимости второго закона Ньютона в релятивистском случае. Релятивистский импульс. Основной закон релятивистской динамики. Закон сохранения импульса.
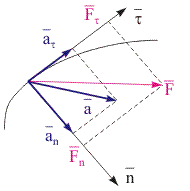Рис. 17.1. Взаимное расположение векторов силы и ускорения относительно СО S.	О применимости второго закона Ньютона в релятивистском случае. Рассмотрим движение частицы, происходящее под действием силы F. Анализ проведем относительно двух ИСО S и S', движущихся относительно друга друга со скоростью V. Систему S' выберем таким образом, чтобы в исследуемый момент времени частица относительно нее покоилась υ' = 0, т.е. система S' являлась бы сопровождающей. В качестве второй системы S выберем произвольную  ИСО. Для ИСО S' справедлив второй закон Ньютона в виде F' = m·a', где m - масса частицы в сопровождающей СО. Таким образом, относительно S' частица под действием силы F' движется с ускорением a' и масса является мерой инертности. Запишем закон движения частицы относительно сопровождающей СО, разложив движение на тангенциальную и нормальную составляющие: 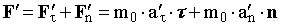.     (17.1) В выражении (17.1) тангенциальное направление свяжем с направлением относительной скорости движения V сопровождающей СО. Отметим, что вектор V равен вектору скорости частицы υ в системе S. Используя соотношения (16.11), (16.12) и учитывая, что aτ - продольная составляющая ускорения, а an - его поперечная составляющая, преобразуем уравнение (17.1) к виду: 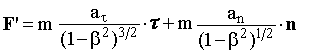,    (17.2) где β = V/c - отношение скорости движения сопровождающей СО  к скорости света, причем V = υ и β = υ/c. Рассмотрим соотношение (17.2) как результат действия силы F, приложенной к частице в ИСО. Согласно классической формулировке второго закона Ньютона F = m·a правую часть выражения (17.2) можно трактовать как сумму тангенциальной и нормальной составляющих силы, действующей на частицу в СО S: 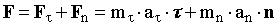.    (17.3) Величины mτ и mn, выполняющие роль меры инерции частицы в СО S в продольном и поперечном направлениях, назовем соответственно продольной и поперечной массой. 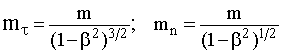.    (17.4) Из уравнения (17.4) следует, что величины mτ и mn не равны друг другу, поскольку имеют разную зависимость от коэффициента β, и следовательно - от скорости частицы υ. Это отличие начинает все более существенно проявляться по мере приближения υ к скорости света. Различный характер зависимости продольной и поперечной массы от скорости подтвержден в экспериментах по движению заряженных частиц в ускорителях (циклотронах). Поскольку величины mτ и mn как коэффициенты пропорциональности между соответствующими составляющими векторов силы и ускорения в СО S различны, то ускорения, которые приобретает частица, двигаясь в направлении действия силы и в перпендикулярном ей направлении, также различны. Исходя из вышеизложенного, относительно системы S направление вектора ускорения в общем случае не совпадает с направлением вектора силы F (см. рис. 17.1) и  второй закон Ньютона в классической форме a = F/m не является абсолютным по отношению к выбору ИСО. Он имеет ограниченную область применимости и справедлив лишь для случая малых скоростей движения частиц ( << c) в ИСО.
	Попытаемся получить такое уравнение динамики материальной точки, чтобы оно в соответствии с принципом относительности Эйнштейна оставалось неизменным в любых ИСО. Для вывода этого уравнения запишем выражение (17.3) в виде (17.5) и проведем его дальнейшие преобразования: 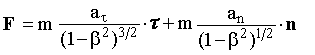.    (17.5) Исходя из определения ускорения, имеем: 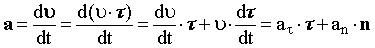,   (17.6) Из (17.6) и (17.5) следует, что: 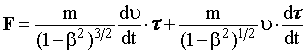             ,    (17.7) Путем дифференцирования можно доказать справедливость следующего выражения: 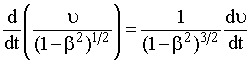.    (17.8) Из уравнений (17.7-17.8) следует, что: 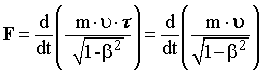.     (17.9) Величина, равная: pрел = m·/(1 - 2)1/2 = ·m·,   (17.10) где  = υ/c называется релятивистским импульсом.
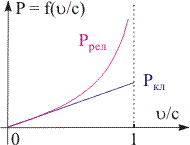Рис. 17.2. Зависимость релятивистского импульса части-цы от ее скорости.	Релятивистский импульс. Установим физический смысл вектора pрел. Для этого обобщим понятие классического импульса на четырехмерный (релятивистский) случай. Естественным обобщением понятия трехмерного вектора импульса p = m· в евклидовом пространстве будет четырехмерный вектор P в пространстве Минковского. P = m·dR/dt0 = {Pt, Px, Py, Pz},     (17.11) где d R = {c·dt, dx, dy, dz} - 4-вектор расстояния в пространстве Минковского. Поскольку P есть комбинация инвариантов массы m0, собственного времени dt0 и 4-вектора dR, то он является 4-вектором. Физическая величина P, задаваемая выражением (17.11), называется 4-вектором энергии-импульса. Исходя из (17.11) пространственные проекции ковариантной величины  4-вектора энергии-импульса  образуют трехмерный вектор pрел, называемый релятивистским импульсом: pрел = {m·dx/dt0, m·dy/dt0, m·dz/dt0} = = m·dr/dt0 = ·m·dr/dt = ·m·.     (17.12) В отличие от классического случая релятивистский импульс зависит от скорости движения частицы не по линейному закону (см. рис. 17.2). Чем ближе скорость частицы к скорости света, тем больше отклонение релятивистского импульса от классического. Тем не менее классический и релятивистский импульсы имеют ряд общих черт: сохраняются для свободных частиц, т.к. согласно определению (17.12), если  = const, то и pрел = const; являются аддитивными величинами; совпадают по величине и направлению при малых скоростях движения частиц.
Станфордский линейный ускоритель [11].	Основной закон релятивистской динамики. Воспользовавшись уравнением (17.9) и определением релятивистского импульса (17.12), получим основной закон релятивистской динамики (релятивистское уравнение движения): F = dррел/dt.     (17.13) Скорость изменения релятивистского импульса частицы равна результирующей всех сил, действующих на нее. Из уравнения (17.9) следует, что за счет действия конечной силы можно получить лишь конечное приращение скорости, т.е. невозможно разогнать частицы до скоростей, равных скорости света. В современных ускорителях удается разогнать заряженные частицы до значений , приближающихся к скорости света и отличающихся от нее всего на доли процента. Уравнение движения (17.13) по форме совпадает с основным уравнением классической динамики F = dp/dt. Однако его физический смысл иной. В правой части уравнения (17.13) стоит производная от релятивистского импульса частицы, зависящего от ее скорости не по линейному закону (17.12). Основной закон релятивистской динамики позволяет по известной зависимости скорости изменения релятивистского импульса определить силу, действующую на частицу, или, зная силу и воспользовавшись начальными условиями, решить задачу о нахождении зависимости r(t). Основной закон релятивистской динамики инвариантен по отношению к выбору ИСО, а ИСО инвариантны по отношению к основному закону релятивистской динамики, что удовлетворяет принципу относительности Эйнштейна. В релятивистском случае, в отличие от классического, сила зависит от выбора ИСО, т.е. не является абсолютной величиной. Как будет показано в дальнейшем (17.37), она видоизменяется в соответствии с преобразованиями Лоренца.
	Закон сохранения релятивистского импульса системы. Рассмотрим систему, состоящую из невзаимодействующих частиц. Проведя суммирование уравнений типа (17.13) по всем объектам системы, получим уравнение, аналогичное (17.13), но уже относящееся ко всей системе в целом. Скорость изменения релятивистского импульса системы невзаимодействующих частиц равна векторной сумме всех сил, действующих на нее. Отсюда вытекает закон сохранения релятивистского импульса, справедливый для частиц, движущихся с произвольными скоростями, и применимый в любых системах отсчета: Релятивистский импульс замкнутой системы невзаимодействующих частиц сохраняется. В этом заключается еще одно сходство релятивистского и не-релятивистского импульса. Закон сохранения импульса является фундаментальным и справедлив не только для механических систем.