1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 3. Взаимосвязь массы и энергии. Энергия связи Энергия связи. § 4. Сила в релятивистском случае Понятие релятивистского вектора силы. Релятивистским моментом импульса частицы называется величина, равная векторному произведению радиус-вектора на релятивистский им Об ограниченности модели несвободной частицы.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 3. Взаимосвязь массы и энергии. Энергия связи

Соотношение между массой и энергией и ее фундаментальный характер.
Понятие энергии связи.
Дефект массы.

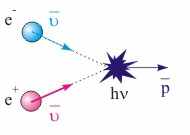Рис. 17.4. Рождение гамма-кванта при столкновении электрона и протона	Соотношение между массой и энергией и его фундаментальный характер. Уравнение (17.19) связывает две важнейшие характеристики материи - энергию и массу. Соотношение (17.19) является одним из фундаментальных законов физики. Оно демонстрирует возможность реализации перехода вещество - поле (см. рис. 17.4). Фундаментальный характер соотношения (17.23) заключается в эквивалентности (равенстве с точностью до постоянного множителя) различных по своему проявлению фундаментальных физических величин - массы и энергии. Поскольку в соответствии с законом сохранения энергия может переходить из одной формы в другую, то не только изменение кинетической энергии вызывает соответствующее изменение массы. В частности, нагревание тела, вызывающее увеличение его внутренней энергии, также приводит к соответствующему изменению его массы. Однако для макроскопических тел эти изменения очень малы и зафиксировать их в эксперименте не удается. Так как соотношение между массой и энергией получено исходя из постулатов теории относительности и преобразований Лоренца, то все эксперименты, подтверждающие их справедливость, говорят в пользу выполнения соотношения между массой и энергией и наоборот. Из соотношения (17.19) следует, что сохранение и аддитивность релятивистской энергии означает сохранение и аддитивность инертной массы, что характерно для классической физики. Обратимся еще раз к трактовке величины массы. В классической физике масса m выступает как мера инертности тела и мера гравитационного взаимодействия. В релятивистской механике величина массы выступает в качестве характеристики, задающей связь между релятивистскими энергией и импульсом. Уточним ее физический смысл. Согласно выражению (17.21) квадрат 4-вектора P равен: P2 = Pt2 - Px2 - Py2 - Pz2 = E2/c2 - p2рел.     (17.26) Поскольку величина P2 есть инвариант, то его значения в произвольной и собственной СО будут равны, т.е. P2 = P02 = E02/c2 = m2·c2.     (17.27) Из выражений (17.26) и (17.27) следует, что масса m есть инвариантная величина, что подтверждается экспериментально. При этом она обладает фундаментальным свойством, а именно масса с точностью до постоянного множителя определяет квадрат длины 4-вектора энергии-импульса. m2·c2 = P2 = E2/c2 - p2рел. (17.28) Значение массы не зависит от направления вектора P в пространстве Минковского и значений релятивистской энергии и импульса. Исходя из выражения (17.28) значение массы частицы можно получить, проведя независимые измерения ее релятивистской энергии и импульса, а сама масса задает связь между релятивистскими энергией и импульсом. Следовательно, в замкнутых ИСО законы сохранения энергии и импульса выполняются одновременно, что в конечном итоге является проявлением свойств однородности и изотропности пространства и времени единого четырехмерного мира событий. Наличие в природе материальных объектов с массой равной нулю, но обладающих энергией и импульсом, явилось несомненным успехом релятивистской механики. К таким физическим объектам относятся, в частности, световые кванты - фотоны. Наличие у фотонов импульса и энергии продемонстрировано в опытах русского физика Петра Николаевича Лебедева. В общей теории относительности показано, что существование у физических объектов компонент 4-вектора энергии-импульса, отличных от нуля, обуславливает наличие их гравитационного поля. Таким образом, гравитационному взаимодействию подвержены как объекты, имеющие массу, так и объекты, не обладающие таковой. Например, траектория света в околозвездном пространстве искривляется вследствие гравитационного взаимодействия звезды и фотонов.
	Энергия связи. Если частицы, составляющие тело, связаны между собой какими-то силами (между ними существует взаимодействие), то сумма их релятивистской энергии и энергии взаимодействия Eвз должна быть меньше энергии покоя. E + Eвз < m·c2.    (17.29) Действительно, при удалении частиц на бесконечность энергия их взаимодействия станет равной нулю, и релятивистская энергия согласно выражению (17.29) должна быть меньше энергии покоя частиц, что невозможно, поскольку энергия покоя есть та минимальная энергия, которой они обладают. Если предположить, что справедливо обратное неравенство E + Eвз > m·c2, то это было бы возможно. Следовательно, неравенство (17.29) есть условие образования связанных состояний. Неравенство (17.29) можно представить в виде: E - m·c2 + Eвз < 0; Eк + Eвз < 0.  (17.30) Энергия связи равна сумме релятивистской кинетической энергии и энергии взаимодействия частиц. Энергия связи всегда отрицательна Eсв < 0, что является условием связанного состояния.  Рассмотрим, каким образом наличие энергии связи влияет на энергию ядра атома. Энергия ядра любого атома Eяд всегда меньше суммы энергий покоя его протонов E0p и нейтронов E0n. Действительно, энергия ядра равна сумме энергии покоя, релятивистской кинетической энергии и энергии взаимодействия образующих его нуклонов: Eяд = E0 + Eк + Eп= E0 + Eсв. Поскольку энергия связи отрицательна, то Eяд < E0 = E0n + E0p.     (17.31)
	Дефект массы. Учитывая уравнение (17.31) и соотношение между массой и энергией (17.19), можно записать выражение для расчета массы ядра: Mяд = M0n + M0p - M,     (17.32) где Mяд, M0n и M0p - массы покоя ядра,  его нейтронов и протонов соответственно, M = |Eсв|/c2 < 0 - величина, называемая дефектом массы. Действительно, результаты измерений масс ядра, протонов и нейтронов показали, что уравнение (17.32) справедливо, т.е. масса ядра всегда меньше суммы масс покоя составляющих его нуклонов. Этот вывод теории относительности нашел свое применение при создании источников атомной энергии и ядерного оружия.
§ 4. Сила в релятивистском случае Понятие релятивистского вектора силы. Преобразования Лоренца для силы и импульса.
	Понятие релятивистского вектора силы. Как известно, наличие внешних воздействий приводит к изменению характеристик состояния тел. Независимо от наличия воздействий на частицу, в каждый момент времени она обладает релятивистскими импульсом, энергией и моментом импульса. Релятивистским моментом импульса частицы называется величина, равная векторному произведению радиус-вектора на релятивистский импульс Lрел. Lрел = [r, ррел].    (17.33) В модели несвободной частицы предполагается, что характеристики самого тела (частицы), например, его масса, линейные размеры, внутреннее строение и т. п. - не изменяются. При этом в любой момент времени частица обладает характеристиками свободной частицы (релятивистскими энергией, импульсом и моментом импульса), а роль внешнего воздействия сводится только к изменению этих характеристик. Несвободную частицу, таким образом, можно использовать в качестве зонда, определяющего характеристики внешних воздействий и степень их влияния на изменение характеристик состояния самой частицы. Об ограниченности модели несвободной частицы. В реальности модель несвободной частицы не является всеобщей, т.к. изменение состояния частиц может оказывать обратное влияние на внешние поля. В данном случае масса как характеристика, определяющая степень влияния на частицу, является весьма неопределенной величиной, и, следовательно, уравнения динамики будут несправедливы. Эйнштейн в общей теории относительности предложил использовать модель искривленного пространства, сохранив при этом справедливость основного уравнения динамики. Степень искривления определяется свойствами пространства, зависящими от интенсивности взаимодействия физических объектов системы.
	Исходя из определений релятивистского импульса и энергии следует, что ррел = υ·E/c2.    (17.34) Согласно выражениям (17.28) и (17.33) такие характеристики несвободной частицы, как релятивистская энергия и релятивистский момент импульса, измеренные в некоторый момент времени, определяются величиной релятивистского импульса. Продифференцировав по времени соотношения (17.28) и (17.33), можно доказать, что изменение значений релятивистской энергии частицы и момента импульса Lрел зависит от скорости изменения релятивистского импульса частицы. Продифференцировав выражение (17.28) по времени, получим: 2E·dE/dt - 2c2·ррел·dррел/dt = 0 или dE/dt = (c2/E)·ррел·dррел/dt. Подставив в последнее уравнение выражение для скорости (17.34), получим, что скорость изменения релятивистской энергии равна: dE/dt = υ(t)·dррел/dt. (17.35) Проведя дифференцирование по времени выражения (17.33) и учтя соотношение (17.34), получим, что скорость изменения релятивистского момента импульса равна: dLрел/dt = [dr/dt, ррел] + [r, dррел/dt] = . = [υ, ррел] + [r, dррел/dt] = = [ррел, ррел]·c2/E + [r, dррел/dt] = [r, dррел/dt]. (17.36) Из уравнений (17.33) и (17.34) следует, что быстрота изменения релятивистской энергии и момента импульса несвободной частицы определяются скоростью изменения релятивистского импульса. Таким образом сила есть величина, определяющую степень влияния внешнего воздействия на характеристики частицы, равная вектору скорости изменения релятивистского импульса, F = dррел/dt. Преобразования вектора силы при переходе от одной ИСО к другой можно найти, воспользовавшись связью между скоростями изменения релятивистского импульса и энергии в этих системах. Исходя из системы уравнений (17.22) и выражения для собственного времени dt0 = dt' = dt/γ, найдем проекции скорости изменения релятивистского импульса: dрx/dt = γ·(dрx'/dt) = γ·(dрx'/dt')·(dt'/dt) = dрx'/dt'; dрy/dt = (dрy'/dt) = (dрy'/dt')·(dt'/dt) = (dрy'/dt')/γ; dрz/dt = (dрz'/dt) = (dрz'/dt')·(dt'/dt) = (dрz'/dt')/γ. Тогда в соответствии с определением силы получим следующие выражения для преобразования ее проекций в различных ИСО: Fx = Fx'; γ·Fy = Fy'; γ·Fz = Fz'.    (17.37)

• Бутиков Е. И., Кондратьев А. С. Физика. Кн.1. Механика. - М.: Наука, 2000. -  326 с.
  
• Иродов И. Е. Механика. Основные законы. - М.: Лаборатория базовых знаний, 2000. - 320 с.
  
• Иродов И. Е. Задачи по общей физике. - М.: Лаборатория базовых знаний, 2001. - 432 с.
  
• Киттель Ч., Найт У., Рудман М. Механика. - М.: Наука, 1975. - 480 с.
  
• Матвеев А. Н. Механика и теория относительности. - М.: Высшая школа, 1986. - 415 с.
  
• Савельев И. В. Курс общей физики. - М.: Наука, 1982. - Т. 1. - 431 с.
  
• Сивухин Д. В. Общий курс физики. - М.: Наука, 1974. - Т. 1. - 519 с.
  
• Стрелков С. П. Механика. - М.: Наука, 1975. - 569 с.
  
• Суханов А. Д. Фундаментальный курс физики. - М.: Агар, 1996. - Т. 1. - 536 с.
  
• Хайкин С. П. Физические основы механики. - М.: Наука, 1971. - Т. 1. - 751 с.
  
• Physics for Scientists and Engineers / by P. M. Fishbane, S. Gasiorowich and S. T. Thornton. Prentice Hall. 1993. V. 1. - 645 p.
  
• Иллюстративный энциклопедический словарь. - М.: БРЭ. 2000. - 1039 с.
  
• Большая советская энциклопедия / Под ред. А. П. Прохорова - М.: Советская энциклопедия. 1969.