1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
| 1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени. Относительность пространства и времени. Материальная точка. Процедуры измерения характеристик пространства и времени. Инвариантность пространственных и временных интервалов в классической физике. Свойства пространства и времени. Принцип симметрии. | |
 Рис. 1.1. Взлет космического корабля "Шаттл". Изменение положения корабля, пламени и клубов дыма происходит во времени и по отношению к пространству, окружающему стартовую площадку. Фото NASA Kennedy Space Center Affairs Office все течет, все изменяется | Понятия пространства и времени. Из своего опыта вы знаете, что все в окружающем нас мире изменяется, причем эти изменения носят двоякий характер. С одной стороны, происходит движение физических объектов друг относительно друга или их трансформация, а с другой - сами объекты изменяются с течением времени. В природе описанные явления существуют в единстве. Приведем лишь несколько примеров: взлет космического корабля со стартовой площадки (см. рис. 1.1), ссылка скрыта, движение планет вокруг Солнца, ссылка скрыта, таяние льда. Изменения, происходящие с телами во времени, могут иметь место и независимо от их перемещения в пространстве. Например, в течение года характерным образом изменяется окружающая нас природа, при нагревании происходит изменение цвета металла. Пространство и время представляют собой категории, предназначенные для описания свойств физического мира. Пространство отражает такие свойства материальных объектов, как протяженность и порядок взаимного расположения. Время отражает такие свойства процессов, как последовательность и длительность. Пространство и время бесконечны. Говорить о пространстве без наличия в нем материальных объектов бессмысленно, точно так же, как бессмысленно говорить о времени в отсутствие каких-либо процессов. Каждое из этих понятий относительно, материя существует в пространстве (относительно пространства), процессы происходят во времени (относительно времени). |
 Часы как инструмент для измерения временных интервалов мгновения, мгновения, мгновения... | Процедура измерения времени. Однородность времени. Поскольку понятия пространства и времени являются фундаментальными (они не могут быть введены через другие, более простые понятия), то зададим процедуры их измерений путем численного выражения свойств этих категорий. На начальном этапе не будем акцентировать внимание на том, что пространственные и временные отношения взаимосвязаны друг с другом. В качестве инструмента для измерения времени выберем часы, основные требования к которым заключаются в равномерности, периодичности и воспроизводимости хода. Примеры часов: маятник, совершающий автоколебания, движение Земли вокруг Солнца, колебания атомов в узлах кристаллической решетки. Наиболее точный инструмент для измерения времени - атомные часы, излучающие электромагнитные волны определенной частоты. Эталон времени - секунда, равная 9,192,631,770 периодам излучения радиоактивного изотопа цезий-133 между определенными подуровнями его основного состояния. Для математического описания временных отношений введем понятие мгновения. Мгновение - физически бесконечно короткий временной интервал или интервал, длительность которого много меньше длительности любых других процессов в рассматриваемой задаче. Примем произвольное мгновение за начало отсчета и сопоставим ему значение переменной t0 = 0. Любому другому мгновению в соответствии с показаниями часов можно сопоставить числовое значение tA, отражающее момент времени наступления некоторого события A, или временную координату на оси Ot. Очевидно, что эта величина относительна, поскольку зависит от выбора начала отсчета. Независимой (инвариантной) характеристикой временных отношений по отношению к выбору начала отсчета является временной интервал t, равный длительности промежутка между мгновениями, отвечающими началу и концу какого-либо процесса, t = t2 - t1 > 0. Другими словами, длительность любого конкретного временного интервала, соответствующего событиям, происходящим при одинаковых условиях, не зависит от значения времени, фиксируемого по часам. Т.е. временной масштаб не изменяется и секунда всегда остается секундой независимо от абсолютного значения времени, фиксируемого с помощью часов. Промежутки времени инвариантны по отношению к выбору начала его отсчета. В этом выражается важнейшее свойство времени - однородность. Однородность времени проявляется в неизменности физических законов по отношению ко времени проведения испытания. Опыт, поставленный в одинаковых условиях, в разные моменты времени дает одинаковые результаты. Другим важным свойством времени является его однородность. Это свойство проявляется в том, что для указания момента наступления какого-либо события или его длительности достаточно одного числа.  |
 Положение материальных объектов в пространстве по отношению к наблюдателю - фотографу. Фото Дмитрия Охримчука | Процедура измерения характеристик пространства. Свойства пространства. Ориентироваться в окружающем мире можно только относительно расположенных в нем предметов. Любые физические объекты находятся на некотором расстоянии друг от друга и занимают определенную область пространства. Типичным примером этого являются фотографии, на которых фиксируется взаимное расположение объектов относительно объектива камеры (наблюдателя). |
 Рис. 1.2. Линейка как инструмент для задания положения физических объектов в пространстве вариант инвариант | Пространственные отношения характеризуем с помощью инструмента - линейки, на которой через равные отрезки, соответствующие эталону длины или его части, нанесены деления (см. рис. 1.2). В качестве эталона длины в системе СИ выбран 1 метр, равный расстоянию, которое преодолевает свет, испускаемый радиоактивным изотопом цезий-133, в вакууме за 1/299,792,458 секунды. Для задания положения тела в пространстве используем физическую модель материальной точки. Материальной точкой (частицей) называется тело, размерами которого можно пренебречь по сравнению с другими характерными размерами, рассматриваемыми в данной задаче. В приведенном выше примере измерений с помощью линейки размер такого тела должен быть мал по сравнению с наименьшим делением ее шкалы. Примем положение произвольной частицы, относительно которой будем производить измерения, за начало отсчета и сопоставим ему значение переменной x0 = 0. Любой другой частице или определенной части тела сопоставим число - пространственную координату xA, соответствующую их положению относительно линейки и выраженную в единицах ее шкалы. Поскольку пространственные координаты зависят от выбора начала отсчета, то они относительны. |
 Рис. 1.3. Декартова система координат | Окружающий нас физический мир, а следовательно, и пространство являются трехмерными, т.е. для задания положения материальной точки в пространстве необходимо указать три числа. В большинстве случаев для этого удобно использовать трехмерную декартову систему координат (СК), имеющую три взаимно перпендикулярные пространственные оси. Вид трехмерной СК приведен на рис. 1.3. Положение материальной точки А в Декартовой СК в произвольный момент времени задается тремя независимыми пространственными координатами {x, y, z}. Положение точки А можно также задать направленным отрезком вектором OA, проведенным из начала отсчета в точку расположения частицы. Он называется радиус-вектором r (см. рис. 1.3). Модуль этого вектора равен: r = (x2 + y2 + z2)1/2. (1.1) Кратчайшее расстояние между двумя произвольными материальными точками A и B, или величина пространственного интервала r, находится по теореме Пифагора: r = (x2 + y2 + z2)1/2. (1.2) Направление от одной частицы к другой задается через направляющие косинусы (косинусы углов между направлением вектора r и соответствующими осями координат): cos 1 = x/r; cos 2 = y/r; cos 3 = z/r. (1.3) Система координат, в которой положение точки задается с помощью двух углов , , указанных на рис. 1.3, и радиус-вектора r, называется сферической. На практике используют также полярные координаты, в которых положение материальной точки задается в виде комбинации ее проекции на вертикальную ось Z, кратчайшего расстояния от точки до этой оси и угла , задающего направление на точку в плоскости, перпендикулярной оси Z. |
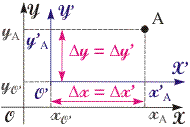 Рис. 1.4. Об инвариантности пространственного интервала (длины вектора O'A) по отношению к изменению положения тела отсчета | Рассмотрим вопрос о влиянии выбора начала отсчета (точки O) на величину пространственного интервала O'A = r' (см. рис. 1.4). Исходя из рис. 1.4 и выражений (1.2) и (1.3), видно, что инвариантными (неизменными) величинами по отношению к операции сдвига СК являются разности проекций, пространственный интервал и направляющие косинусы. В частности, длина одного и того же отрезка будет неизменной в любой области пространства, где бы он ни располагался. Например, эталон одного метра всегда останется таковым независимо от его местонахождения. Пространственный интервал r - инвариантен по отношению к выбору начала отсчета, что обусловлено таким свойством пространства, как однородность. Однородность пространства проявляется в независимости физических законов от положения исследуемой системы в пространстве. Опыт, поставленный в одинаковых физических условиях, в разных местах дает одинаковые результаты. |
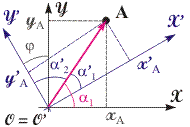 Рис. 1.5. Об инвариантности величины пространственного интервала (длины вектора O'A) по отношению к изменению выбора направления осей системы координат | Рассмотрим, как влияет на величину разности проекций вектора O'A ориентация осей координат, начало которой связано с точкой O = O' (см. рис. 1.5). Из геометрических соображений и тригонометрических преобразований следует справедливость системы уравнений (1.4): x' = x·cos + y·sin ; y' = x·cos - y·sin ; z' = z; r' = r. (1.4) Действительно, из рис. 1.5 видно, что r = r'; cos '1 = cos(1 - ); cos '2 = y'/r' = (r'·sin '1)/r' = sin(1 - ). Тогда выполняются следующие соотношения: x' = r'·cos 1' = r·cos(1 - ) = r·(cos 1·cos + sin 1·sin ); y' = r'·cos 2' = r·sin(1 - ) = r·(sin 1·cos - cos 1·sin ). Учитывая, что r·cos 1 = x, а r·sin 1 = y, получим доказываемые уравнения (1.4). Таким образом, пространственный интервал r является инвариантом по отношению к операции поворота осей СК, что обусловлено таким свойством пространства, как изотропность. Важно отметить, что разность проекций вектора r на оси координат, задающая его величину согласно (1.2), не является инвариантом. Изотропность пространства, в частности, проявляется в том, что длина одного и того же отрезка не зависит от его ориентации в пространстве (выбора направления осей координат). Изотропность пространства, в целом, проявляется в независимости физических законов от ориентации физической системы в пространстве. Принцип симметрии. Инвариантность пространственных и временных интервалов является отражением свойств симметрии физического мира. В рассмотренных выше примерах симметрия наблюдается по отношению к операциям сдвига начала СК и поворота осей координат. Первое из перечисленных свойств симметрии обусловлено однородностью пространства и времени, а второе изотропностью пространства. Базирующийся на этих свойствах принцип симметрии выполняет существенную роль в объяснении свойств физического мира. Он по своей сути является методологическим принципом, задающим направление познавательного процесса (см. темы 8, 10 и 16).  |
| § 2. Системы отсчета Процедуры измерения временных и пространственных интервалов с учетом единства пространственно-временных отношений. Системы отсчета и их роль в физике. Способы синхронизации часов.  | |
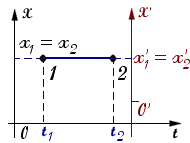 Рис. 1.6. Одноместное измерение временных интервалов. Индекс 1 соответствует началу процесса, индекс 2 его завершению Рис. 1.6. Одноместное измерение временных интервалов. Индекс 1 соответствует началу процесса, индекс 2 его завершению | Одноместное измерение времени. Обратимся к единым пространственно-временным отношениям и попытаемся установить способы определения величин временных и пространственных интервалов, необходимые для описания изменения положения физических объектов. Логично предположить, что для корректного описания состояния физических объектов в пространстве и времени необходимо производить одноместное измерение временных и одновременное измерение пространственных интервалов. Одноместное измерение временных интервалов означает, что снятие показаний часов должно производиться в одной точке пространства, в которой начинается и заканчивается некий процесс (см. рис. 1.6). Операция одноместного измерения времени не вызывает проблем, если размером часов в любой точке пространства можно пренебречь. Из рис. 1.6. видно, что если измерение заданного временного интервала t происходит в одной точке пространства, то независимо от выбора положения начала отсчета величина t постоянна. Если процесс начинается и заканчивается в разных точках пространства, то предварительно необходимо провести операцию синхронизации часов, расположенных в этих точках. |
 Рис. 1.7. Одновременное измерение координат объекта (пространственных интервалов). В качестве объекта выбран стержень, расположенный вдоль оси OX | Одновременное измерение координат означает, что для определения размеров физических объектов координаты их крайних точек необходимо измерять в один и тот же момент времени по часам, расположенным в месте локализации этих частей объекта (см. рис. 1.7). Из рис. 1.7 видно, что выбор начала отсчета времени не влияет на длину объекта (в нашем примере стержня). Принципиальным условием, без которого нельзя ввести понятие длины движущихся объектов, является необходимость предварительного согласования показаний часов или проведение операции синхронизации часов, находящихся в разных точках пространства, т. к. измерение времени в соответствии с рассматриваемым подходом нужно производить в тех точках, где располагается объект измерений (например, крайние точки стержня). Как уже упоминалось, проведение операции синхронизации необходимо также для измерения временного интервала, соответствующего длительности событий, которые происходят в разных точках пространства. Естественный способ согласования - способ переноса - представляет собой процесс предварительной синхронизации показаний множества часов, сосредоточенных в одной точке пространства, с последующим их переносом по всему пространству. Этот вариант имеет существенный недостаток, поскольку приводит к разным результатам в зависимости от способа переноса, в частности, его скорости.  |
| | Процедура синхронизации часов способом сигналов. Предложим другой способ. Для синхронизации часов, расположенных в разных точках, необходим обмен информацией об их показаниях (например, с помощью светового сигнала). Поместим дополнительные часы посередине между точками A и B, обозначив ее С. Из этой точки в момент времени tc1 испустим сигнал в направлении A и B. Исходя из результата целого ряда физических экспериментов и постулата о постоянстве скорости света (см. тему 15), скорость светового сигнала не зависит от направления его распространения. Реализуем ситуацию, когда расстояния AС и BС будут одинаковы и равны x/2, а в точках A и B без задержки и изменения величины скорости происходит его отражение. Тогда: x/2 = |xB - xC| = |xA - xC| = V0·(/2), где V0 - скорость распространения сигнала, - промежуток времени от испускания до возвращения сигнала в точку C. На рис. 1.8 приведен график движения, соответствующий распространению светового сигнала. Положения С1 и С2 на рис. 1.8 отображают точку С в моменты времени tc1 и tc2. 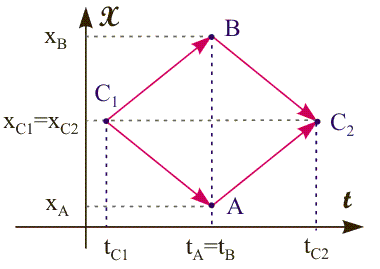 Рис. 1.8. Схема синхронизации часов способом сигналов Прибытия сигналов в точки A и B являются событиями одновременными, так же как и их возвращение в С. Действительно,  В нашем опыте регистрация момента времени происходит с помощью одних и тех же часов в одном и том же месте пространства точке С, следовательно, измерив величину , можно ввести понятие одновременности удаленных событий в A и B, которое определяется временем прихода в них сигнала и равняется (tc1 + tc2)/2. |
| ТО+СК+ часы=СО | Системы отсчета. Перейдем к описанию механического движения - простейшего вида движения, заключающегося в изменении положения тел в пространстве с течением времени. Как мы уже показали, положение частицы в пространстве относительно, т. к. определяется выбором начал отсчета пространственной и временной координаты. Следовательно, механическое движение зависит от этих начальных условий. Более того, положение тела в пространстве можно указать только относительно других тел. Невозможно найти физический способ задания положения тела в пустом пространстве. Т.о. для описания движения необходимо начало отсчета СК связать с каким-либо другим телом. Само движение исследуемых объектов будет происходить относительно этого тела. Обусловленность вида механического движения выбором начальных условий является проявлением принципа относительности в механике. Рассмотрим положение исследуемых тел относительно условно неподвижного тела, которое назовем телом отсчета (ТО). Для задания положения исследуемых тел свяжем ТО с началом отсчета выбранной СК. Для описания движения относительно этой СК в каждой точке пространства расположим часы, показания которых предварительно были синхронизованы. Другими словами, для описания положения тел в пространстве и их движения необходимо выбрать систему отсчета (СО). Система отсчета система, состоящая из тела отсчета, связанной с ним системы координат и синхронизованных часов. |
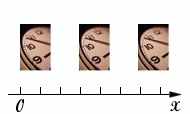 Рис. 1.9. Вид СО, используемой для описания одномерного движения  Управляемый аппарат, планируемый для запуска на Марс в 2003-2004 годах. Фото California Institute of Technology. ссылка скрыта | Вид СО, используемой для описания одномерного движения, приведен на рис. 1.9. В общем случае трехмерного движения процедура задания положения материальной точки несколько сложнее. Пример. Проиллюстрируем последовательность задания положения тел в пространстве на примере составления карты поверхности Марса. Выбор СО с точки зрения решения задачи кинематики, конечно, произволен и физические явления (в частности, движение) будут выглядеть в них по-разному. Но, несмотря на это, как мы покажем в дальнейшем, сущность физических законов в соответствии с принципом относительности останется неизменной по отношению к выбору СО. Поэтому с точки зрения кинематики систему отсчета целесообразно выбирать так, чтобы движение по отношению к ней описывалось максимально просто. При этом сама СО выполняет роль инструмента для изучения законов механического движения.  |
| § 3. Единство пространственно-временных отношений и их отражение в мире событий Описание единых пространственно-временных отношений в случае одномерного движения. Понятие двумерного мира событий. График одномерного движения или мировая линия в двумерном мире событий. Отражение единства пространственно-временных отношений в четырехмерном мире событий.  | |
| | Описание единых пространственно-временных отношений в частном случае одномерного движения. Двумерный мир событий. Использование СО дает возможность наблюдать за положением частицы в пространстве в разные моменты времени, но не позволяет наглядно следить за динамикой этого процесса. Для устранения этого недостатка введем понятие мира событий. Рассмотрим сначала частный случай одномерного (прямолинейного) движения. Каждому событию, задающему положение частицы в произвольный момент времени в некоторой специальным образом заданной системе координат, соответствуют два числа {xA, tA}, которые играют роль пространственно-временных координат этого события. Таким образом, мы переходим к взаимосвязанному описанию пространственно-временных отношений на плоскости Xt, т.е. к описанию движения в двумерном мире событий.  |
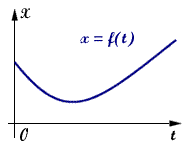 Рис. 1.10. Мировая линия (график движения) в двумерном мире событий.  Сложный (неодномерный) характер движения шмеля. “Полет шмеля”. Фото Алексея Хаскина | График одномерного движения. Пусть с течением времени положение материальной точки в пространстве изменяется. Это соответствует изменению ее положения в мире событий. Ввиду непрерывности времени данная последовательность точек в мире событий также непрерывна и их можно соединить линией, которая называется мировой линией (МЛ). График движения x = f(t), или мировая линия в двумерном мире событий, представляет собой непрерывную последовательность пространственно-временных координат частицы, отраженную на плоскости Xt. Вид МЛ в некотором произвольном временном интервале для случая прямолинейного движения приведен на рис. 1.10. В наиболее простом варианте движения частицы - одномерном движении с постоянной скоростью, график движения представляет собой прямую. Обратите внимание на то, что для корректного описания движения время необходимо измерять по часам, расположенным в той точке пространства, где происходит событие, и поэтому в каждой точке на оси X должны быть свои часы и своя ось времени. Но поскольку часы синхронизованы, то на рис. 1.10 изображена только одна из этих временных осей, связанная с телом отсчета. Движение частицы всегда сопровождается возрастанием времени, что соответствует ее перемещению вдоль МЛ в мире событий (см. рис. 1.10) слева направо. Это утверждение справедливо для любых СО независимо от выбора начала отсчета. Обратим внимание на одну интересную особенность. В природе существует целый ряд процессов, называемых обратимыми. Рассмотрим в качестве примера колебания груза на пружине в отсутствие сопротивления. Груз при движении в разных направлениях проходит через одни и те же положения без изменений в окружающем мире. Если заснять движение груза на кинопленку и прокрутить ее в обратном направлении, то наблюдатель, глядя на экран, не сможет установить факт изменения направления прокручивания пленки в кинопроекторе, т.е. характер движения не изменился. Законы обратимого движения инвариантны по отношению к выбору направления хода времени, что является проявлением принципа симметрии (симметрии по отношению к отражению в точке, расположенной на оси времени).  |
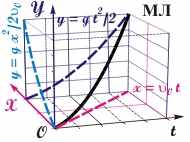 Рис. 1.11. Пример вида мировой линии в трехмерном мире событий | Понятие четырехмерного мира событий. Движение в общем случае трехмерно. Для его описания по аналогии с двумерным миром событий введем понятие четырехмерного мира событий XYZt. Такое представление, с одной стороны, адекватно описывает единые пространственно-временные отношения, а с другой позволяет, как мы увидим в дальнейшем, выявить истинные инварианты преобразований для СО, движущихся с произвольными скоростями, в том числе близкими к скорости света (см. тему 16). Отметим, что в таком подходе к описанию движения имеется существенный недостаток. Четырехмерное пространство невозможно представить. Поэтому обычно рассматривают проекции мировых линий на пространственно-временные плоскости Xt, Yt, Zt и чисто пространственные плоскости XY, XZ, YZ. Пример. На рис. 1.11 представлена мировая линия тела, брошенного под углом к горизонту с начальной скоростью 0. Проекция МЛ на плоскости Xt, Yt представляет собой графики движения: y = g·t2/2; x = 0·t. Проекция МЛ на плоскость XY дает графическое изображение траектории y = g·(x2/2·02). Обратим внимание на особенности анализа пространственно-временных отношений. Периодическое движение частицы, являющееся основой простейших часов, задается через понятие "пространственный интервал", который, в свою очередь, определяется через характеристики движения, задаваемые с помощью понятия "промежуток времени" (расстояние, на которое распространяется свет за определенное время). Это еще раз напоминает о том, что природа единое многообразие пространственно- временных отношений. В ней мы имеем дело с принципиальными отношениями в мире событий XYZt.  Отредактировано:  |

| § 1. Способы описания движения Понятия радиус-вектора и вектора перемещения. Об инвариантности скалярных и векторных величин в физике. Векторный, естественный и координатный способы описания движения материальной точки. Путь и траектория. Понятия средней и мгновенной скорости и ускорения. Скорость прохождения пути. Эквивалентность векторного, естественного и координатного способов описания движения. | | ||||||||||||
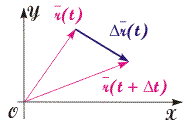 Рис. 2.1. К определению вектора перемещения 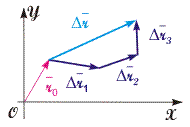 Рис. 2.2. Результат серии последовательных перемещений частицы | Понятие вектора перемещения. Остановимся на подходе к описанию движения в трехмерном пространстве относительно СО, которую мы условно примем за неподвижную. Положение произвольной материальной точки (частицы) в пространстве в момент времени t можно задать в виде направленного отрезка, называемого радиус-вектором r, который проведен из начала координат (от тела отсчета) к этой точке (см. рис. 2.1). При движении материальной точки в пространстве ее радиус-вектор изменяется. Приращение радиус-вектора r за конечный промежуток времени t (рис. 2.1) называется перемещением. Перемещение как физическая величина обладает рядом свойств, характерных для векторов.
Для того, чтобы подчеркнуть векторный характер физической величины r ее обычно называют вектором перемещения. | | |||||||||||
| | Об инвариантности законов физики, выраженных через скалярные и векторные величины. Чтобы величина могла быть описана вектором, для нее, так же, как и для вектора перемещения, должны выполняться следующие операции:
Физические законы, записанные в форме скаляров и векторов, являются инвариантными по отношению к выбору начала отсчета и поворота осей координат СО. Другими словами, физические законы, выраженные через скалярные и векторные величины или их комбинации, равноправны по отношению к выбору СК (величины векторов и их взаимная ориентация не изменяются).  | | |||||||||||
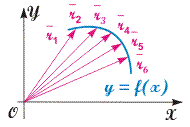 Рис. 2.3. Иллюстрация векторного способа описания движения (двумерное движение)  Рис. 2.4. Иллюстрация естественного способа описания движения (двумерное движение) 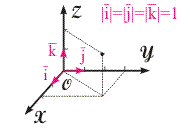 Рис. 2.5. Иллюстрация координатного способа описания движения | Способы описания движения в пространстве. Пусть скалярные f и векторные величины A зависят от времени: f = f(t), A = A(t). Поведение скалярной величины задается обычной аналитической зависимостью f(t). В случае векторов дело обстоит сложнее. Существуют несколько способов выражения зависимости A = A(t):
Векторный способ описания движения заключается в нахождении величины и направления радиус-вектора r в любой момент времени, т. е. установлении вида зависимости r(t) = r(t)·er(t), где r(t) - модуль радиус-вектора, er(t) - единичный вектор, задающий направление вектора r. er = r/r = {cos 1; cos 2; cos 3}; (2.1) cos i - направляющие косинусы или косинусы углов между радиус-вектором и осями декартовой системы координат, рассчитываемые согласно (1.3). В случае плоского (двумерного) движения направление обычно задается в виде значения тангенса угла между вектором r и осью OX. Исходя из определения, вектор перемещения r задается как изменение (приращение) радиус-вектора r, произошедшее за время t (см. рис. 2.2): r = r(t + t) - r(t). (2.2) Вектором средней скорости называется величина, равная отношению приращения радиус-вектора к промежутку времени, в течение которого оно произошло. Важно отметить, что средняя скорость не дает полной информации о движении, т. к. относится к определенному промежутку времени t и ее значение зависит от величины этого промежутка. Вектор средней скорости сонаправлен вектору перемещения. Отметим, что длина вектора средней скорости и вектора перемещения не равны друг с другу. Эти величины имеют разную размерность и измеряются в разных единицах (соответственно в метрах на секунду и метрах). Для описания движения в конкретный момент времени воспользуемся понятием мгновенной скорости, которая равна пределу отношения приращения радиус-вектора к промежутку времени t, за который оно произошло при устремлении к нулю величины этого промежутка или производной от вектора перемещения по времени dr/dt: 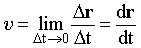 . (2.3) . (2.3) | | |||||||||||
 Траектория электрического разряда (молния) | Мгновенная скорость показывает, как быстро изменяется радиус-вектор материальной точки при бесконечно малом приращении времени t для выбранного момента t. Движение с постоянной скоростью называется равномерным. Воображаемая непрерывная линия, по которой перемещается материальная точка в пространстве, называется траекторией. | | |||||||||||
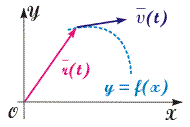 Рис. 2.6. Расположение радиус-вектора r и вектора мгновенной скорости материальной точки по отношению к траектории y(x) (положение векторов указано в некоторый произвольный момент времени применительно к двумерному движению) | Движение по траектории может происходить в любом направлении в отличие от движения частицы вдоль мировой линии. Уравнения траекторий в плоскостях XY, XZ, YZ можно получить путем исключения переменной t из зависимостей x(t), y(t), z(t) (см. задачи). Исходя из определения, вектор скорости направлен по касательной к траектории (см. рис. 2.6). Это утверждение справедливо для любой точки траектории. По аналогии с понятием скорости введем понятие векторов среднего и мгновенного ускорений. Вектором среднего ускорения называется величина, равная отношению приращения вектора скорости к промежутку времени, в течение которого оно произошло. aср = /t. (2.4) Мгновенное ускорение равно пределу, к которому стремится среднее ускорение при t, стремящемуся к нулю или производной от вектора скорости по времени.  . (2.5) . (2.5)Движение с постоянным ускорением называется равнопеременным. Если вектор ускорения сонаправлен вектору скорости, то движение называется равноускоренным, если вектора скорости и ускорения направлены в противоположные стороны, то равнозамедленным. В общем случае вектор мгновенного ускорения сонаправлен вектору приращения скорости, а не скорости, т.о. его ориентация по отношению к траектории движения определяется характером изменения вектора скорости. Зная зависимость скорости от времени, можно найти вектор перемещения частицы r. Для этого необходимо воспользоваться определением (2.3):  . (2.6) . (2.6)Естественный способ описания движения. В каждом конкретном случае движения радиус-вектор частицы очерчивает в пространстве определенную траекторию, по которой и перемещается частица. Расстояние, пройденное частицей вдоль траектории назовем путем. Путь скалярная величина, которая всегда положительна. Путь, пройденный частицей за конечный промежуток времени t = t0, задается выражением:  . (2.7) . (2.7)Согласно уравнениям (2.6) и (2.7), путь величина, в общем случае не равная модулю вектора перемещения. Их количественное совпадение наблюдается только для прямолинейного движения частицы в одном направлении. Средняя скорость прохождения пути s ср, согласно определению, равна: s ср = s/t. (2.8) Можно показать, что среднее значение модуля скорости равно: 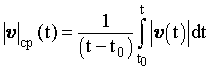 . (2.9) . (2.9)Исходя из уравнений (2.7)(2.9), следует, что: s ср = ||ср. (2.10) | | |||||||||||
| | Координатный способ. Введем характеристики для координатного способа описания движения. Положение, а следовательно, и движение частицы в пространстве можно описать с помощью проекций радиус-вектора на оси координат. В общем случае таких проекций будет три {x, y, z}. Радиус-вектор частицы можно выразить через эти проекции и единичные вектора. r(t) = x(t)·i + y(t)·j + z(t)·k = {x, y, z}, (2.11) где i, j, k - единичные вектора, направленные вдоль осей координат: i = {1,0,0}; j = {0,1,0}; k = {0,0,1}. Исходя из изотропности пространства, направления вдоль осей OX, OY, OZ равноправны. Таким образом, для частицы, перемещающейся в трехмерном пространстве, число степеней свободы (число независимых координат, определяющих положение физического объекта в пространстве) равно трем. Поскольку оси координат равноправны, то задав способы описания движения относительно одной из них, мы сможем полностью охарактеризовать движение в трехмерном пространстве. Величина x, равная производной от координаты по времени x = dx/dt, (2.12) называется проекцией мгновенной скорости частицы на ось OX и характеризует движение частицы вдоль этой оси. В общем случае приращение координаты dx за бесконечно малый промежуток времени dt зависит от положения частицы относительно оси OX в данный момент времени. На практике часто используется понятие проекции средней скорости, равной: x ср = dx/dt. (2.13) По аналогии с определением проекции скорости введем понятия проекций мгновенного ax и среднего ускорений ах ср: ах = dx/dt, (2.14) ах ср = x/t. (2.15) Отметим, что вектора скорости и ускорения, так же как вектор перемещения, можно выразить через их проекции и единичные вектора i, j, k: = x·i + y·j + z·k; (2.16) a = ax·i + ay·j + az·k. (2.17) Соотношение (2.16) не является формальным. Если частица участвует одновременно в нескольких движениях, то каждое из них независимо. При этом для нахождения результирующей скорости частицы скорости отдельных ее движений складываются как вектора. Заметим, что координатный способ подчеркивает единство пространственно-временных отношений, поскольку мгновенная скорость определяется непосредственно из мировой линии в двумерном мире событий, отражающем это единство. Эквивалентность различных способов описания движения. Поскольку мы имели дело с описанием одного и того же движения различными способами, то их результаты должны быть эквивалентными. Действительно, величина вектора перемещения и его направление однозначно связаны с приращениями координат в соответствии с уравнениями (1.2) и (1.3). С другой стороны, траекторию движения, а следовательно и путь можно найти, исключив время из уравнений движения для пространственных проекций радиус-вектора. Таким образом, векторный, естественный и координатный способы описания движения эквивалентны.  | | |||||||||||
| § 2. Задача кинематики. Характеристики состояния материальной точки Подходы к решению задачи кинематики. Расчет графика движения по его характеристикам (случай прямолинейного движения). Характеристики состояния материальной точки. Понятие фазовой траектории.  | | ||||||||||||
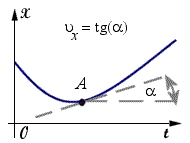 Рис. 2.7. Мировая линия и мгновенная скорость частицы в двумерном мире событий | Подходы к решению задачи кинематики. Задача кинематики состоит в описании механического движения вне зависимости от причин, его вызывающих. Движение материальной точки задано, если известна мировая линия (графики движения) или заданы характеристики, с помощью которых можно найти МЛ. Попытаемся задать вид МЛ следующим образом: сначала экспериментальным путем найдем характеристики движения на определенных его этапах (частные характеристики), а затем, используя их, зададим графики движения в целом. Такой подход предполагает наличие этих частных характеристик в произвольный момент времени. Обоснуем правомочность такого подхода к описанию движения. Непрерывность МЛ означает наличие в любой момент времени не только определенного значения координаты частицы, но и ее производной. В общем случае вектор перемещения dr за бесконечно малый промежуток времени dt, а следовательно, и величина мгновенной скорости зависят от времени (координат частицы A в четырехмерном мире событий) и однозначно определяются видом МЛ. На графике одномерного движения это проявляется в изменении тангенса угла, образуемого касательной к МЛ и осью Ot (см. рис. 2.7). Вид МЛ также однозначно задает средние значения векторов скорости материальной точки. Более того, определив вектора мгновенной скорости в различные моменты времени, можно найти вектора среднего и мгновенного ускорений. Нахождение характеристик движения применительно к определенным моментам времени основано на уравнении (2.7). Итак, такие характеристики движения, как мгновенные скорость и ускорение, и дополнительные характеристики, как путь, средняя скорость и средняя скорость прохождения пути, обусловлены видом МЛ. Попытаемся найти графики движения, зная его частные и дополнительные характеристики. Для простоты рассмотрим случай прямолинейного движения. Поиск уравнения движения по его характеристикам (случай прямолинейного движения). Решим задачу, воспользовавшись координатным способом. Покажем, что описать движение координатным способом, т.е. найти зависимости x(t), y(t), z(t), можно, предварительно определив соответствующие функции проекций скорости от времени x(t), y(t), z(t). Проанализируем частный случай - произвольное прямолинейное движение частицы относительно условно неподвижной системы отсчета S. В мире событий такое движение описывается графиком движения x = f(t) или непрерывной мировой линией произвольной формы. Перейдем к поиску графика движения по известной зависимости скорости от времени. Из определения скорости найдем величину конечного перемещения частицы x за промежуток времени t: 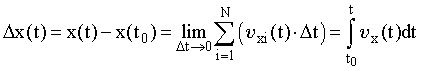 . (2.18) . (2.18)Следовательно, положение частицы в любой момент времени задается уравнением:  . (2.19) . (2.19)Аналогичным образом получается выражение для расчета скорости частицы, исходя из зависимости ее ускорения от времени: 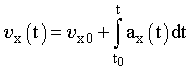 . (2.20) . (2.20) | | |||||||||||
 Равноускоренное движение мячика, движущегося в поле силы тяжести [11] | В случае равнопеременного движения ax = const и, следовательно, зависимость x(t) будет линейной функцией времени: x(t) = x0 + ax·t. (2.21) Подставив выражение (2.21) в (2.20), получим уравнение равнопеременного движения частицы: x(t) = x0 + x0·t + ax·t2/2. (2.22) Значение пути s, пройденного частицей за время t = t - t0, можно найти, исходя из уравнения: 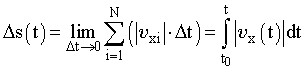 . (2.23) . (2.23)Используя полученные выражения и определения средней скорости x ср и средней скорости прохождения пути s ср, найдем выражения для их расчета через зависимость мгновенной скорости от времени:  . (2.24) . (2.24) . (2.25) . (2.25) | | |||||||||||
| | Характеристики состояния частицы. Мы убедились в том, что, если задан график движения, то прямолинейное движение описано полностью. Аналогично, если задана мгновенная скорость в любой момент времени, то с точностью до постоянной можно найти график движения. В реальном эксперименте мы можем измерить значения координат и скоростей в некоторые конкретные моменты времени. Однако поскольку мировая линия непрерывна, то этих данных достаточно для определения положения материальной точки в любой момент времени и изменения этого положения во времени, т.е. для описания ее движения. Действительно, пусть для произвольного движения в условно неподвижной СО в некоторый момент времени ti известны шесть величин компонент векторов r и , равных {x(ti), y(ti), z(ti), x(ti), y(ti), z(ti)}. Зная их можно найти эти значения в следующий момент времени ti + t. Следовательно, исходя из характера изменения этих компонент во времени, можно найти зависимость r(t), т.е. описать движение. Отметим, что найденная таким образом зависимость r(t) получится тем точнее, чем ближе будет значение суммы приращения проекции радиус-вектора в выражении (2.18) к значению интеграла. Следовательно, состояние материальной точки в мире событий задается ее координатами и проекциями скоростей. Радиус-вектор и вектор скорости являются характеристиками состояния материальной точки, однозначно определяющими ее движение. | | |||||||||||
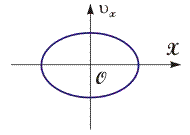 Рис. 2.8. Пример фазовой траектории. Гармонические колебания пружинного маятника | Понятие фазовой траектории. Поскольку радиус-вектор и вектор скорости являются характеристиками состояния материальной точки, то, найдя зависимости координат материальной точки от соответствующих проекций ее вектора скорости, в частности, x(x), мы полностью опишем движение. Линия, отображающая зависимость проекции скорости от соответствующей координаты, называется фазовой траекторией. Примеры. Фазовая траектория материальной точки в случае ее прямолинейного равноускоренного движения представляет собой параболу, симметричную относительно оси OX. Фазовая траектория пружинного маятника, совершающего гармонические колебания вдоль оси OX, представляет собой замкнутую траекторию - эллипс (см. рис. 2.8). Движение материальной точки относительно неподвижной СО мы научились задавать. Для нахождения кинематических характеристик физических объектов в любых СО, а не только в той, которую мы примем за условно неподвижную, необходимо сначала описать движение тел отсчета, а затем воспользоваться законами преобразования кинематических характеристик при переходе между этими СО. Движение ТО можно описать, воспользовавшись моделью материальной точки, связанной с телом отсчета, но закон преобразования характеристик состояния частиц нам предстоит получить.  | | |||||||||||
| § 3. Абсолютные величины в классической механике. Преобразования Галилея. Закон преобразования скоростей Абсолютный характер временного интервала в классической механике. Преобразования Галилея. Абсолютный характер пространственного интервала в классической механике. Законы преобразования скоростей и ускорений.  | | ||||||||||||
| движение относительно, пространство и время абсолютны | Абсолютный характер временного интервала в классической механике. Рассмотрим две движущиеся относительно друг друга СО. В качестве часов в обеих СО используем однотипные устройства. Синхронизацию часов в этих СО проведем методом сигналов. В качестве сигнала используем движение произвольной частицы с постоянной скоростью, много большей относительной скорости движения систем отсчета. Ввиду быстроты распространения сигнала часы обеих систем могут быть синхронизованы между собой указанным выше способом, поскольку за время распространения сигнала СО существенно не изменятся относительно друг друга. Следовательно, время наступления одного и того же события, а также промежутки времени между началом и концом одного и того же процесса в этих СО будут равны t = t', т.е. временной интервал является абсолютной величиной по отношению к выбору СО (не зависит от того, движется она или покоится). | | |||||||||||
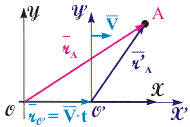 Рис. 2.9. Иллюстрация закона преобразования радиус-векторов частицы при описании ее движения в разных ИСО | Преобразования Галилея. Выявим связь между пространственными координатами в неподвижной относительно наблюдателя - лабораторной СО (ЛСО) S и СО S', движущейся относительно нее равномерно прямолинейно. Пусть СО S' движется в положительном направлении вдоль оси OX с постоянной скоростью V относительно лабораторной (неподвижной по отношению к наблюдателю) СО (см. рис. 2.9). Как видно из рис. 2.9, для любого момента времени можно записать выражение, связывающее радиус-вектор r' частицы A в подвижной и лабораторной СО: x'A = xA - x'0 = xA - V·t. (2.26) Спроецировав это уравнение на оси координат и учтя возможность проведения синхронизации часов в этих системах отсчета методом сигнала, получим прямые и обратные преобразования Галилея: x' = x - V·t; y' = y; z' = z; t' = t; x = x' + V·t; y' = y; z' = z; t' = t. (2.27) Из преобразований Галилея вытекает следующее:
 Иллюстрация инвариантности пространственного интервала (длины покоящейся относительно берега яхты) x в движущихся (A и B) и покоящейся (C) СО. Регата “Бархатная осень 2001”. a.ru/~istok/BO2001/Foto/BO2001.htm  | | |||||||||||
| | Абсолютный характер пространственного интервала. Пусть СО S' движется относительно системы S с переменной скоростью V(t), много меньшей скорости света. По аналогии с выражением (2.26) можно записать, что радиус-векторы произвольных точек A и B в этих СО связаны между собой следующими соотношениями: 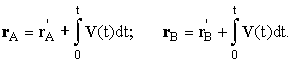 Из этих соотношений следует, что величина пространственного интервала r = |r| не зависит от выбора СО: |r'| = |r'B - r'A| = |rB - rA| = |r|. Пространственный интервал в классической механике есть абсолютная величина по отношению к выбору СО. | | |||||||||||
| | Закон преобразования скоростей. Скорости частицы при переходе от описания движения в одной СО к описанию движения в другой изменяются в соответствии с векторным уравнением, называемым законом преобразования скоростей: = ' + V, (2.28) где - абсолютная скорость (скорость частицы относительно ЛСО); ' - относительная скорость (скорость частицы относительно движущейся СО); V - переносная скорость (скорость движения системы S' относительно ЛСО). Равенство (2.26) получается, исходя из принципа независимости перемещений. Действительно, вектор перемещения относительно ЛСО r равен векторной сумме перемещения r' материальной точки относительно СО S' и перемещения R тела отсчета системы S' относительно ЛСО. r = r' + R. (2.29) Поделив выражение (2.29) на элементарный временной интервал dt и воспользовавшись определением мгновенной скорости, получим закон преобразования скоростей (2.28). Из однородности времени, однородности и изотропности пространства, а также инвариантности относительно преобразований Галилея вытекают обобщения повседневного опыта и удается выявить характеристики пространственно-временных отношений, не зависящие от выбора СО. Ими являются временные и пространственные интервалы. Из выражения (2.29) следует, что относительные скорости материальных точек не зависят от выбора СО, т.е. также являются абсолютными величинами. ' = 'B - 'A = B - A = . | | |||||||||||
| | Закон преобразования ускорений. Если все точки СО S' движутся с одинаковым переносным ускорением aс относительно лабораторной СО, то, дифференцируя по времени выражение (2.28), получим закон преобразования векторов ускорений между этими системами: a' = a - aс, (2.30) где a - абсолютное ускорение; a' - относительное ускорение; aс - переносное ускорение. Если СО S' движется относительно ЛСО равномерно прямолинейно, то ускорение не зависит от выбора СО. В общем случае ускорение относительно, т.е. определяется выбором СО. | | |||||||||||

