1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
§ 2. Годограф скорости
Годограф. Представление движения с помощью годографа скорости.
Описание криволинейного движения частицы: понятие радиуса кривизны траектории, нормального и тангенциального направлений.

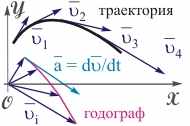
Рис. 3.7. Годограф скорости
Понятие годографа. Наглядное представление о характере движения частицы дает кривая, называемая годографом скорости. Введем его определение. Для этого изобразим вектора скорости частицы в произвольные моменты времени, переместив их начала в одну точку (см. рис. 3.7). Затем проведем линию, соединяющую концы этих векторов. Полученная линия называется годографом скорости.
Годограф скорости представляет собой воображаемую линию, по которой с течением времени перемещается конец вектора скорости.
Примеры.
 | Прямолинейное равноускоренное движение . Годограф представляет собой прямую линию. |
 | Движение тела, брошенного под углом к горизонту. Годограф - прямая линия, параллельная вектору g. |
 | Равномерное движение по окружности. Годограф - окружность. |
 | Движение по окружности с постоянным ускорением. Годограф - плоская спираль. |
Годограф по отношению к вектору скорости выполняет ту же роль, что и траектория по отношению к радиус-вектору (эти понятия были введены аналогично). Поэтому вектора скорости и ускорения в пространстве скоростей являются соответствующими аналогами радиус-вектора и скорости в обычном трехмерном пространстве.
Рассмотрим вопрос об ориентации вектора ускорения по отношению к траектории, воспользовавшись понятием годографа. Ускорение направлено по касательной к годографу точно так же, как вектор скорости направлен по касательной к траектории. Таким образом, вектор ускорения сориентирован произвольным образом по отношению к вектору скорости (см. рис. 3.7) и, следовательно, под произвольным углом (от - до ) к траектории движения. Как будет показано в дальнейшем, вектор ускорения всегда направлен внутрь траектории движения частицы.
Пользуясь понятием годографа, можно найти значение ускорения частицы |a| в случае ее равномерного движения по окружности радиусом r со скоростью . Для этого рассчитаем величину периода кругового движения частицы. Она окажется равным T = 2r/. Движение скоростной точки вдоль годографа происходит с тем же значением периода, который равен T = 2/a. Следовательно, величина вектора ускорения частицы в рассматриваемом случае рассчитывается по формуле a = 2/r.
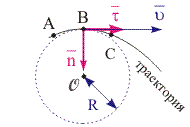
Рис. 3.8. Соприкасающаяся окружность. Нормальное и тангенциальное направления при криволинейном движении (пунктиром изображена соприкасающаяся окружность)
Понятие радиуса кривизны и нормального и тангенциального направлений. Рассмотрим, от чего зависит ориентация вектора ускорения по отношению к траектории при криволинейном движении частицы.
Выделим на произвольном участке траектории некоторые точки A, B, C (см. рис. 3.8.) Из геометрии известно, что через три точки, не лежащие на одной прямой, можно провести окружность. Эта окружность и траектория в общем случае не совпадают. Далее начнем приближать точки A и C к B. Радиус окружности при этом будет изменяться, и она постепенно сблизится с траекторией. Предельное значение радиуса, при котором они совпадут, назовем радиусом кривизны траектории R, а саму окружность - соприкасающейся. Величину, обратную радиусу кривизны 1/R, назовем кривизной траектории в точке B, а центр соприкасающейся окружности - центром кривизны траектории в точке B.
Заметим, что каждая точка траектории имеет свои значения радиуса и центра кривизны.
Выделим два направления в пространстве: нормальное и тангенциальное, совпадающие соответственно с направлениями вдоль радиуса к центру соприкасающейся окружности и вдоль касательной к траектории (см. рис. 3.8). Единичные вектора, сориентированные вдоль этих направлений, обозначим соответственно как n и . Причем вектор всегда сонаправлен вектору скорости . Следовательно,
= ·. (3.17)

