1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 4. Кинематика твердого тела Абсолютно твердым телом называется физический объект, расстояния между любыми точками которого с течением времени не изменяются. Поступательным движением называется такой вид движения тела, при котором все его точки перемещаются по параллельным траекториям. Вращение тела вокруг закрепленной оси. Вращение тела вокруг закрепленной точки. Прецессия как пример движения тела вокруг закрепленной точки. Любое плоское движение можно представить как совокупность поступательного и вращательного движений. Например, при скатывании цилиндра по наклонной плоскости она проходит через точку касания цилиндра и плоскости

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 4. Кинематика твердого тела

Абсолютно твердое тело. Виды движения твердых тел.
Поступательное и вращательное движения - основные виды движения абсолютно твердого тела.
Вращение тела вокруг закрепленной оси.
Вращение тела вокруг закрепленной точки.
Плоское движение твердого тела. Понятие мгновенной оси вращения.

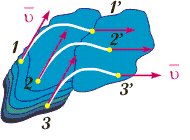
Рис. 3.11. Поступательное движение АТТ

Виды движения твердого тела. Для рассмотрения движения тела воспользуемся физической моделью абсолютно твердого тела (АТТ).

Абсолютно твердым телом называется физический объект, расстояния между любыми точками которого с течением времени не изменяются.

 Существуют различные возможные виды его движения:

	поступательное;
	вращательное вокруг закрепленной оси;
	вращательное вокруг закрепленной точки;
	плоское;
	произвольное свободное движение.

Независимыми видами движения являются первые два, а остальные три могут быть представлены как их комбинации.

Поступательным движением называется такой вид движения тела, при котором все его точки перемещаются по параллельным траекториям.

Заметим, что в общем случае эти траектории не обязательно являются прямыми линиями (см. рис. 3.11). Исходя из определения АТТ следует, что в случае его поступательного движения все его точки в каждый момент времени имеют одинаковые значения скоростей и ускорений. Таким образом, данный вид движения может быть описан путем выявления зависимости r = r(t) для любой из его точек, в качестве которой обычно выбирают центр масс (см. тему 6).

 




 

Вращение тела вокруг закрепленной оси. При вращении АТТ вокруг неподвижной оси OZ оно обладает только одной (вращательной) степенью свободы, и все его точки движутся с одинаковой угловой скоростью , направление которой параллельно оси вращения. Вектор  равен:

 _i =  = {0, 0, d/dt}.     (3.28)

Таким образом, движение твердого тела аналогично движению любой из его точек, имеющих соответствующие кинематические характеристики (угловую скорость и ускорение).






 

Вращение тела вокруг закрепленной точки. В случае произвольного движения твердого тела вокруг неподвижной точки положение оси вращения, а следовательно, и направление вектора  изменяются. Вектор угловой скорости в любой момент времени при этом имеет три независимые компоненты:

 = {_x, _y, _z}     (3.29)

и не параллелен вектору углового ускорения. В данном случае движения тело обладает тремя вращательными степенями свободы.

Если АТТ участвует одновременно в нескольких вращательных движениях, то его угловая скорость равна векторной сумме угловых скоростей каждого из них:

 = ₁+ ₂+ ... + _n,     (3.30)

что легко доказать, продифференцировав по времени выражение векторного закона сложения элементарных угловых перемещений:

d = d₁+ d₂+ ... + d_n.       

Таким образом, результат рассматриваемого сложного движения твердого тела эквивалентен вращению тела вокруг оси, проходящей через точку O и параллельной вектору угловой скорости , определяемому из уравнения (3.30).
 





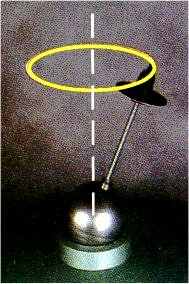
Пример прецессионного движения.

Прецессия как пример движения тела вокруг закрепленной точки. Движение любого вектора, конец которого перемещается по окружности, описывая со временем конус вокруг некоторой оси, не совпадающей с направлением вектора угловой скорости, называется прецессией. Вектор скорости для прецессионного движения равен:

 = dr/dt = [r] = {(-d/dt)·r_y, (d/dt)·r_x, 0}.     (3.31)

Прецессия характерна не только для механических объектов. Она, например, присуща электронным орбитам атомов, помещенных в магнитное поле.







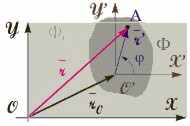
Рис. 3.12. Плоское движение.

Плоское движение твердого тела.

Плоским называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных некоторой неподвижной по отношению к выбранной СО базовой плоскости.

Типичным примером такого рода является качение цилиндра. При описании плоского движения АТТ достаточно найти кинематические характеристики некоторой его части (фигуры) Ф, представляющей собой сечение АТТ плоскостью, параллельной базовой Ф₀ (см. рис. 3.12). Положение твердого тела относительно базовой плоскости и связанной с ней СО S можно задать, указав радиус-вектор r₀ произвольной точки O' этого тела и направление на любую другую его точку, лежащую в плоскости Ф (например, точку A). Указанное направление зададим с помощью угла  (см. рис. 3.12) между горизонтальной осью и вектором r'.

В процессе движения твердого тела радиус-вектор r₀ и угол  изменяются и положение точки A можно задать двумя уравнениями

r₀ = r₀(t) и = (t).

Если за время dt радиус-вектор r' повернется на угол d, то на такой же угол повернется любая другая точка или отрезок твердого тела. Таким образом, движение АТТ относительно точки O' можно рассматривать как чисто вращательное с угловой скоростью , а выбор точки O' является произвольным с точки зрения сохранения вращательного характера этого движения.

Введем вспомогательную СО, жестко связанную с точкой O' АТТ и совершающую поступательное движение относительно системы S (направление осей координат СО S' относительно системы S не изменяется). Вектор элементарного перемещения произвольной точки A относительно СО S можно задать в соответствии с уравнением:

dr = dr₀ + dr',     (3.32)
где dr₀ - вектор элементарного перемещения точки O',
dr' - вектор элементарного перемещения точки A в СО S'.

Продифференцировав выражение (3.32) по времени, учитывая условия выбора системы S' и связь между линейной и угловыми характеристиками (3.9) точки A в системе S', получим:

 = ₀ + [, r'],     (3.33)
где ₀ - вектор скорости поступательного движения
 СО S' относительно S;
 - вектор скорости частицы A относительно СО S;
r' - радиус-вектор точки A в СО S'.

Из уравнения (3.33) следует, что скорость любой точки АТТ можно представить как суперпозицию ее составляющей, связанной с выбором произвольной точки твердого тела - движением точки O' со скоростью ₀, и составляющей ' = [, r'], обусловленной вращением АТТ относительно поступательно движущейся СО S', жестко связанной с точкой O'. Это утверждение применимо и к твердому телу в целом.

Любое плоское движение можно представить как совокупность поступательного и вращательного движений.







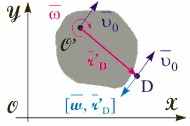
Рис. 3.13. К определению положения мгновенной оси вращения твердого тела

Мгновенная ось вращения. Покажем, что плоское движение в определенных системах отсчета можно свести к чисто вращательному. Исходя из определения плоского движения и рис. 3.13, следует, что вектора, входящие в правую часть уравнения (3.33), параллельны. Таким образом, для любого момента времени всегда найдется такая точка твердого тела D, скорость которой в СО S окажется равной нулю _D = 0, и согласно (3.33) выполнится равенство:

₀ = - [, r'_D],     (3.34)
где r'_D - радиус-вектор точки D в СО S'.

Модуль радиус-вектора r'_D будет равен r'_D = ₀/.

Согласно уравнению (3.34) радиус-вектор точки D задает положение соответствующей оси, относительно которой происходит исключительно вращательное движение твердого тела, причем направление этой оси совпадает с вектором угловой скорости .

Ось вращения, относительно которой любая точка твердого тела в данный момент времени совершает исключительно вращательное движение, называется мгновенной осью вращения.

Положение мгновенной оси меняется с течением времени. Например, при скатывании цилиндра по наклонной плоскости она проходит через точку касания цилиндра и плоскости.

Итак, мы показали, что любое сложное движение твердого тела можно свести к совокупности поступательного и вращательного движений, которые являются базовыми. Их описание можно осуществлять на основе моделей движения частицы.