1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
§2. Описание движения несвободных частиц. Второй закон Ньютона
Описание движения частиц в ИСО при наличии взаимодействия.
Сила как характеристика воздействия на частицу.
Понятие инертной массы. Второй закон Ньютона.


Исаак Ньютон (16431727). Английский ученый физик
Описание движения частиц в ИСО при наличии взаимодействия. В ИСО можно соблюсти все необходимые условия для описания движения: задать СК, выбрать определенный момент времени в качестве начала отсчета, задать временной масштаб, а также провести операцию синхронизации часов. Как мы уже выяснили, в любой ИСО частицы, воздействие на которые любых физических объектов отсутствует, движутся с нулевым ускорением, т.е. равномерно прямолинейно или покоятся.
Перейдем теперь к описанию движения тел в разных ИСО при наличии взаимодействия. Сначала рассмотрим наиболее простой случай - движение частицы, на которую оказывается некоторое воздействие со стороны других тел или частиц. Используем для этого модель несвободной частицы. Согласно данной модели воздействие оказывает влияние на характеристики состояния частицы, но не изменяет ее физические характеристики, например, массу, плотность и т.п.

Иллюстрация понятия "сила" [11]
Для количественного описания движения частицы при наличии воздействия введем понятие силы. Величину силы, действующей на макроскопические объекты, можно измерить различными приборами, например, динамометром, который предварительно прошел операцию калибровки. Показания динамометра, в принципе, определяют результат действия сил любой природы (гравитационной, электромагнитной и т.д.). При этом результат воздействия нескольких сил на динамометр определяется в соответствии с законом сложения векторов (см. рис. 4.3).
За единицу измерения силы в системе СИ принимают 1 ньютон. Размерность силы - [кг·м/с2].
Сила - физическая величина, являющаяся мерой механического воздействия одного тела или поля на другое тело.
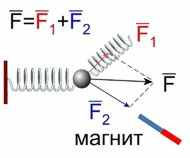
Рис. 4.3. Измерение одновременно действующих сил различной природы с помощью динамометра
Сила обладает следующими свойствами:
 | имеет материальное происхождение, то есть описывает различные взаимодействия, существующие в природе (тепловые, электромагнитные, механические и т.д.). За каждой силой стоит тело или поле, взаимодействие с которым она характеризует; |
 | сила - векторная величина, характеризующаяся величиной, точкой приложения и направлением; |
 | сила, воздействуя на тело, вызывает его ускорение или деформацию (см. рис. 4.3, 4.4). |

Перейдем теперь к описанию движения в ИСО при наличии воздействия. Для этого используем модель несвободной частицы. Согласно этой модели внешнее воздействие оказывает влияние на характеристики состояния частицы, но не изменяет ее физические характеристики, например, массу.
Рассмотрим поведение несвободной частицы с точки зрения динамики, т. е. с учетом причин, вызывающих ее движение. Для количественного описания этого процесса введем понятие силы. Величину силы можно измерить различными приборами, например, динамометром, который предварительно прошел операцию калибровки. Показания динамометра, в принципе, определяют действие сил любой природы, подчиняясь при этом закону сложения векторов (см. рис. 4.3).
За единицу измерения силы в системе СИ принимают 1 ньютон. Размерность силы - [кг·м/с2].
Чем больше сила, тем большее воздействие она оказывает на физические объекты (см. рис. 4.4).
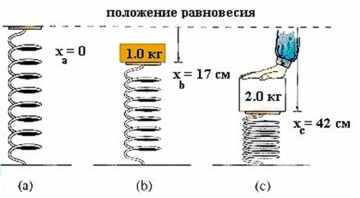
Рис. 4.4. Действие различных сил на пружину (динамометр) [11]


Ньютон и яблоко [11]
О пользе размышлений
Понятие инертной массы. Второй закон Ньютона. Ньютон установил, что ускорение, приобретаемое телом в результате внешнего воздействия, прямо пропорционально силе. Этот экспериментальный факт оказался справедлив для любых тел. Ньютон, обобщив полученные результаты, установил связь между ускорением, приобретаемым частицей, силой, действующей на нее и вызывающей это ускорение, и некой физической величиной, отражающей способность частицы сопротивляться внешнему воздействию. Ньютон назвал эту величину массой. С точки зрения динамики масса задает величину ускорения, которое получает тело под действием определенной силы. Масса является мерой инертности тела по отношению ко внешнему воздействию. Обычно ее называют инертной массой.
Масса является фундаментальной физической величиной. Понятие массы нельзя свести к более простым понятиям. Чем больше масса тела, тем меньшее ускорение оно приобретет под действием одинаковой силы. Чем больше сила, тем с большим ускорением, а следовательно, и большей конечной скоростью будет двигаться тело (см. рис. 4.5).
Рис. 4.5. Иллюстрация понятия массы и второго закона Ньютона [11]
Связь трех величин силы F, ускорения a и массы m, сформулирована во втором законе Ньютона (законе движения), справедливом исключительно в ИСО:
ускорение, приобретаемое частицей при действии на нее произвольных сил, равно отношению векторной суммы этих сил к массе частицы.
В векторной форме второй закон Ньютона имеет следующий вид:
a = Fi/m. (4.1)
Векторное уравнение (4.1) можно представить как 3 скалярных, спроецировав его на оси координат.
При таком рассмотрении второй закон Ньютона утверждает о наличии пропорциональной зависимости между силой, действующей на частицу, и приобретаемым ею ускорением. Масса выполняет роль коэффициента пропорциональности, измеряемого независимым способом.
Массу можно измерить самостоятельно, не используя второй закон Ньютона (см. § 3).
Наличие у частицы с определенной массой ускорения может служить мерой силового воздействия, т.е.
F = m·a,
где F - результирующая сила, действующая на частицу.
ИСО является инвариантом по отношению ко второму закону Ньютона. Действительно, ускорение частицы не зависит от выбора ИСО (2.30), сила определяется взаимным расположением тел и их относительными скоростями, которые так же не зависят от выбора ИСО, а масса есть характеристика частицы, которая в классической механике является постоянной величиной в любых ИСО.

