1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
§ 3. Кинематика криволинейного движения. Полное, нормальное и тангенциальное ускорения
Представление вектора полного ускорения через нормальную и тангенциальную составляющие.
Нормальное ускорение и его физический смысл.
Тангенциальное ускорение и его физический смысл.
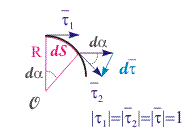
Рис. 3.9. К выводу выражения для расчета величины вектора полного ускорения
Представление вектора полного ускорения через нормальную и тангенциальную составляющие. Рассмотрим вопрос о направлении вектора ускорения частицы при ее криволинейном движении. Исходя из определения вектора мгновенного ускорения и выражения (3.17), получим:
a = d(·)/dt = (d/dt)· + ·(d/dt). (3.18)
Преобразуем второе слагаемое в уравнении (3.18).
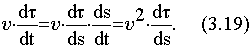
Из рис. 3.9 следует, что |d| = ||·d = d и d = ds/R. Тогда
|d/ds| = 1/R.
С учетом того, что приращение вектора d перпендикулярно нормали (см. рис. 3.9), d/ds = n/R. Следовательно,
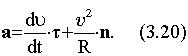
Согласно (3.20), вектор ускорения a равен сумме двух компонент. Первая из них представляет собой его тангенциальную составляющую, а вторая - нормальную составляющую. Вектор a назовем вектором полного ускорения материальной точки, определяющего в общем случае движения величину и направление вектора изменения ее скорости. Величина вектора полного ускорения:
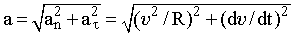. (3.21)
Крутой вираж. При движении мотоциклиста по кривой с переменной скоростью он обладает нормальным и тангенциальным ускорениями
Нормальное ускорение. Определим величину и роль нормального ускорения в изменении скорости. Предположим, что a = an. Тогда:
d = a·dt = an·dt = an·n·dt. (3.22)
Таким образом, вектор приращения скорости d сонаправлен вектору нормального ускорения. Поскольку нормаль n перпендикулярна , а следовательно, и скорости , то вектор приращения скорости в рассматриваемом случае перпендикулярен в любой точке траектории. Следовательно, годограф и траектория движения материальной точки представляют собой окружности. При этом скорость материальной точки изменяется только по направлению, сохраняясь неизменной по величине. Направление вектора приращения скорости в рассматриваемом случае совпадает с вектором n в любой точке траектории. Таким образом,
нормальное ускорение характеризует изменение скорости по направлению.
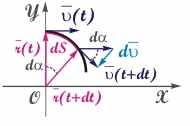
Рис. 3.10. К выводу выражения для расчета величины вектора нормального ускорения
Величину вектора an можно рассчитать из простых геометрических соображений (см. рис. 3.10). Путь ds, пройденный частицей за время dt, можно рассчитать исходя из двух независимых уравнений:
ds = ·dt; (3.23)
s = R·d. (3.24)
Учтя, что d= ·d и исходя из уравнений (3.22)(3.24), получим окончательное выражение для расчета вектора нормального ускорения:
an = d/dt = 2/R или в векторном виде an = (2/R)·n. (3.25)
Тангенциальное ускорение. Определим величину и роль в изменении скорости тангенциального ускорения. Предположим, что a = a. Тогда:
d = a·dt = a·dt, (3.26)
следовательно, в данном случае вектор приращения скорости сонаправлен вектору тангенциального ускорения. С другой стороны, в любой момент времени вектор скорости сонаправлен , поэтому вектора приращения скорости и тангенциального ускорения также направлены вдоль .
Поскольку ориентация вектора скорости не изменяется с течением времени, то модуль приращения вектора скорости |d| равен приращению модуля вектора скорости d|| = d и, следовательно, a = d/dt.
Тангенциальное ускорение характеризует изменение скорости по величине.
Вектор тангенциального ускорения равен:
a = (d/dt)·. (3.27)