Geum.ru

1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материалаДокументы

Содержание


§ 1. Движение частицы по окружности и его кинематические характеристики
Описание движения по окружности.
Угловые кинематические характеристики.
Вектора угловой скорости и ускорения
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   35
§ 1. Движение частицы по окружности и его кинематические характеристики
Движение материальной точки по окружности как движение с одной степенью свободы.
Понятие векторов углового перемещения, угловой скорости и углового ускорения.
Связь угловых кинематических характеристик с линейными.





Вращательное движение звезд в галактике. “Галактика Андромеда”. Фото Jason Ware

Введение. В предыдущих темах мы рассмотрели описание движения частиц или тел отсчета, с ними связанных. Однако важным является также описание движения систем координат, связанных с твердыми телами и служащих для пространственно-временного описания еще одного класса движений, например, различных вращений. Решив эту задачу и воспользовавшись преобразованиями Галилея, можно описать все возможные случаи движения твердых тел в любых системах отсчета.

Перед тем как приступить к изучению кинематики твердого тела, рассмотрим сначала простейший случай  движение его составных частей (материальных точек) по окружности и более общий вариант  криволинейное движение.

Описание движения по окружности. При движении частицы по окружности меняется только направление ее радиус-вектора r(t). Уравнение, характеризующее изменение положения частицы со временем, имеет вид:

r(t) = r·er(t), где r = const.     (3.1)







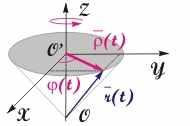
Рис. 3.1. Движение частицы по окружности

Пусть радиус-вектор частицы описывает круговой конус. Тогда его сечение плоскостью ХО'У, перпендикулярной оси OZ, образует окружность радиуса  (см. рис. 3.1). В декартовой СК уравнения движения в проекциях на оси координат примут вид:

x(t) = ·cos (t);  y(t) = ·sin (t),     (3.2)

а траектория частицы будет описываться уравнением:

x2 + y2 = 2.     (3.3)

Вопрос. Какой вид будет иметь мировая линия при равномерном движении частицы по окружности? В рассматриваемом случае угол изменяется со временем по закону (t) = ·t + 0, а мировая линия в трехмерном мире событий будет представлять из себя винтовую линию, нанизанную на ось Ot и имеющую шаг, равный периоду обращения частицы в плоскости вращения T = 2/. В отличии от движения по спирали значение проекции МЛ на ось Ot все время возрастает.







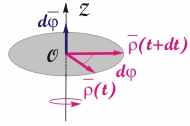
Рис. 3.2. Определение направления вектора элементарного углового перемещения по правилу буравчика (правого винта). Ручку буравчика вращаем по направлению вращения радиус-вектора частицы. Направление вектора d совпадет с направлением поступательного движения буравчика

Угловые кинематические характеристики. Рассмотрим движение частицы в плоскости XY в полярных координатах. Соответствующие уравнения записываются следующим образом:

 = const,  = (t).     (3.4)

В данном случае частица обладает одной степенью свободы и ее движение удобно характеризовать зависимостью угловой координаты (угла) от времени (t).

По аналогии с понятием элементарного вектора перемещения dr введем понятие вектора элементарного углового перемещения d. За величину вектора d примем значение угла, на который повернется частица вокруг оси OZ за время dt, выраженное в радианах. Направление вектора d зададим таким образом, чтобы оно совпадало с осью вращения и определялось в соответствии с правилом правого винта (см. рис. 3.2).

 





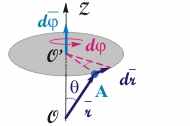
Рис. 3.3. Установление связи между направлением векторов элементарного углового и линейного перемещений

Из вышеизложенного и рис.3.3 следует, что вектора линейного и углового перемещений связаны соотношением (3.5) и не зависят от выбора начала отсчета (точки О) на оси вращения:

dr = [d, r].     (3.5)

Чтобы быть вектором, величина должна удовлетворять четырем правилам (см. тему 2, § 3), одним из которых является подчинение закону сложения векторов.

Рассмотрим случай последовательного поворота частицы на углы d1 и d2 вокруг произвольным образом направленных осей, проходящих через точку О. Элементарное перемещение частицы можно представить как векторную сумму, равную:

dr = dr1 + dr2 = [d1, r] + [d2, r], = [d, r],     (3.6)
где d = d1 + d2.

 





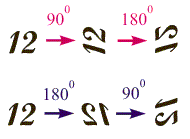
Рис. 3.5. Результаты двух серий однотипных поворотов твердого тела во взаимно перпендикулярных направлениях, проведенных в разной последовательности

Таким образом, последовательность перемещений на элементарные углы подчиняется закону сложения векторов и, следовательно, величины dи  с этой точки зрения могут быть векторами ( d при t ). Перемещения же на конечные углы этому правилу не удовлетворяют (см. примеры).


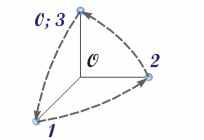
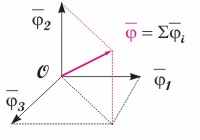
Рис. 3.4. Положение частицы и векторов ее углового перемещения в серии последовательных поворотов на 90 градусов вокруг трех взаимно перпендикулярных осей, проходящих через закрепленную точку

Из рис. 3.3 следует, что при повороте на конечный угол модуль вектора перемещения равен:

|r| = r·sin·2·sin(/2),

и, следовательно, векторное равенство (3.5) в общем случае не выполняется.

Для малых углов поворота оно выполняется приближенно и тем точнее, чем ближе величины 2·sin(/2) и sin( друг к другу.

Итак, введенная величина d в сравнении с понятиями перемещения, скорости и ускорения не является "естественным" вектором (точка приложения dчетко не определена и находится где-то на оси вращения). Кроме того, вектор d имеет существенный ряд ограничений, связанных с малостью поворота. В силу этих причин элементарное угловое перемещение часто называют псевдовектором.






 

Вектора угловой скорости и ускорения. По аналогии с линейной скоростью введем понятие мгновенной угловой скорости. Ею называется величина, равная производной от вектора углового перемещения по времени:

 = d/dt.     (3.7)

Выразим угловую скорость через другие известные нам векторные величины. Модуль линейной скорости равен:

x2 + y2)1/2 = [(-··sin(t))2 + (··cos(t))2]1/2 = ·

 = d/dt.   (3.8)

 





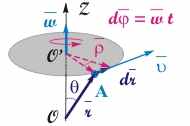
Рис. 3.6. Установление связи между направлением векторов угловой и линейной скорости.

С учетом направлений векторов, указанных на рис. 3.6, скалярное равенство  = · = ·r·sin можно записать в векторном виде:

 = [, r].     (3.9)

Уравнение (3.9) можно получить также, разделив выражение (3.5) на dt и воспользовавшись определениями линейной и угловой скоростей.

Понятие вектора углового ускорения  введем по аналогии с поступательным движением, т. е. как производной от угловой скорости по времени:

 = d/dt.     (3.10)

Установим связь между линейным и угловым ускорением. Для этого продифференцируем выражение (3.11) по времени. Получим, что

a = [, r] + [ [, r]].     (3.11)

В случае неподвижной оси вращения, вектора углового ускорения и угловой скорости коллинеарны (сонаправлены или направлены в противоположные стороны). Первое слагаемое в выражении (3.11) представляет собой составляющую ускорения, направленную по касательной к траектории движения частицы, а второе  вдоль радиуса  в сторону оси вращения (их называют тангенциальной и нормальной составляющими вектора ускорения). Итак, в случае движения частицы по окружности, вектора нормальной и тангенциальной составляющей ускорения равны:

a = [, r],     (3.12)
an = [ [, r]].     (3.13)

Модули величин нормального, тангенциального и полного ускорений частицы рассчитываются из следующих равенств:

a = ·,     (3.14)
an = 2·,     (3.15)
a = (a2 + an2)1/2·(2 + 4)1/2.     (3.16)

Вектор углового ускорения частицы при неизменной ориентации оси вращения параллелен этой оси (направлен вдоль вектора или против него в зависимости от того увеличивается или уменьшается угловая скорость).