1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 2. Релятивистская энергия. Закон сохранения энергии Понятие релятивистской энергии. Релятивистская энергия равна произведению проекции 4-вектора энергии-импульса на скорость света. Для замкнутой системы невзаимодействующих частиц релятивистская энергия остается постоянной.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 2. Релятивистская энергия. Закон сохранения энергии

Понятие релятивистской энергии.
Закон сохранения энергии.
Энергия покоя. Релятивистская кинетическая энергия.

 

Понятие релятивистской энергии. Рассчитаем величину изменения некоторой физической величины, которая обусловлена работой всех сил, действующих на частицу, т.е. является аналогом кинетической энергии в классическом случае. В качестве исходного уравнения движения используем основной закон релятивистской динамики (17.13). Умножив уравнение (17.9) скалярно на вектор скорости частицы υ, получим:

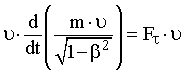.     (17.14)

Проведем ряд преобразований. Путем дифференцирования можно доказать справедливость соотношения:

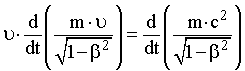.     (17.15)

Из выражений (17.14) и (17.15) следует, что

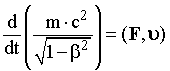.     (17.16)

Умножим уравнение (17.16) на величину dt. Используя выражение для расчета работы всех сил dA на элементарном перемещении dr, получим что:

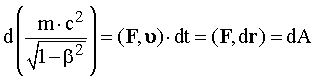.     (17.17)

Согласно (17.17) величина E, равная

E = m·c²/(1 - β²)^1/2 = ·m·c²,

имеет размерность энергии. Рассмотрим физический смысл величины E. Для этого найдем проекцию 4-вектора энергии-импульса на ось времени в пространстве Минковского. Ее величина равна

P_t = m·dR_t/dt₀ = ·m·c·dt/dt = ·m·c.     (17.18)

Таким образом, с точностью до постоянного множителя “c” значение физической величины E равно проекции P_t. Величина E называется релятивистской энергией частицы.

Релятивистская энергия равна произведению проекции 4-вектора энергии-импульса на скорость света.

E = P_t·c = ·m·c².   (17.19)

Проведя суммирование уравнений по всем частицам системы, получим, что за конечный промежуток времени

E = A, т.е.  (17.20)

изменение релятивистской энергии системы равняется работе всех сил, действующих на эту систему.

Рассмотрим как преобразуются релятивистская энергия и импульс при переходе к другим ИСО. Поскольку величины p_рел и E являются проекциями ковариантной величины - 4-вектора энергии-импульса

P = {P_t, P_x, P_y, P_z} = {E·c, p_{рел x}, p_{рел y}, p_{рел z}},     (17.21)

то уравнения их преобразований должны быть аналогичны преобразованиям Лоренца. При этом компоненты p_{рел x}, p_рел y, p_{рел z} преобразуются как x, y, и z, а компонента
P_t = E·c, как время t. Таким образом,

                  
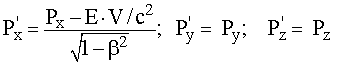
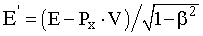     (17.22)



 

Закон сохранения релятивистской энергии. Обобщив выражение (17.20) на систему невзаимодействующих частиц, можно сформулировать закон сохранения энергии в релятивистском случае.

Для замкнутой системы невзаимодействующих частиц релятивистская энергия остается постоянной.

Можно показать, что закон сохранения энергии распространяется также и на случаи распада и столкновения частиц, происходящие в замкнутых ИСО.

Обратите внимание, что энергия взаимодействия в величину релятивистской энергии не входит. Более того, понятие потенциальной энергии, определяемое конкретным видом взаимодействия частиц, в релятивистской механике не используется. Это обусловлено тем, что конечная скорость распространения взаимодействия не позволяет привести в соответствие изменение положения частиц системы и величину потенциальной энергии, определяемой соответствующими силами и зависящей от взаимного расположения частиц, и следовательно, корректно задать значение потенциальной энергии системы применительно к данному моменту времени.




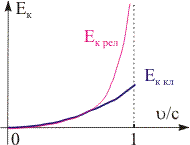
Рис. 17.3. Зависимость релятивистской кинетической энергии от соотношения /c

Энергия покоя. Релятивистская кинетическая энергия. Из определения (17.19) вытекает, что если частица покоится, то ее релятивистская энергия отлична от нуля и рассчитывается с помощью следующего соотношения:

E₀ = m·c².     (17.23)

Величина E₀, равная релятивистской энергии частицы в собственной системе отсчета,  называется энергией покоя частицы.

Энергия покоя включает в себя все виды энергии, не связанные с движением тел, в частности, внутреннюю энергию.

Разность релятивистской энергии и энергии покоя позволяет выделить энергию, обусловленную исключительно движением частицы, т.е. релятивистскую кинетическую энергию E_к.

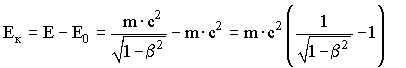.    (17.24)

Разложив в ряд формулу (17.24), можно показать, что выражение для расчета релятивистской кинетической энергии частицы при малых скоростях совпадает с полученной в классической механике формулой E_к = m·υ²/2.

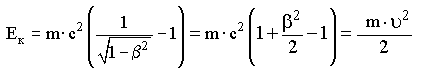.    (17.25)

Из выражений (17.19) и (17.24) следует, что релятивистская кинетическая энергия частицы в отличие от классического случая неограниченно возрастает при стремлении скорости  к скорости света (см. рис. 17.3).

Согласно (17.24)

релятивистская энергия частицы представляет собой сумму энергии покоя и релятивистской кинетической энергии.

Изменение релятивистской кинетической энергии в соответствии с (17.17) и (17.24) равно работе всех сил, действующих на систему. Это утверждение совпадает с аналогичным законом для классической физики.

Релятивистская энергия зависит от выбора ИСО, т.к. равна сумме инварианта E₀ и неинвариантной величины E_к. Поскольку для общего случая совокупности свободных частиц, движущихся с произвольными скоростями, невозможно найти ИСО, в которой бы они все покоились, то именно релятивистская энергия является фундаментальной физической величиной, сохраняющейся в замкнутых ИСО.

Отметим, что для макроскопических тел энергия покоя много больше возможных изменений кинетической энергии. Энергия может переходить из одной формы в другую (см. рис. 17.4), сохраняясь при этом в замкнутых системах невзаимодействующих частиц.

Пример. Генерация гамма-кванта при аннигиляции электронно-позитронной пары. Эксперимент показал, что релятивистская энергия гамма-кванта E = h·, являющаяся по сути энергией электромагнитной волны, равна сумме релятивистских энергий электрона и позитрона, представляющих собой сумму их энергий покоя и энергии механического движения (релятивистскую кинетическую энергию).