1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 2. Пространственно-временной интервал как абсолютная характеристика мира событий Относительность временных и пространственных    интервалов. Пространственно-временной интервал. Абсолютность пространственно-временного интервала по отношению к выбору ИСО. Эйнштейн ввел новый инвариант I, являющийся комбинацией величин r и t, характеризующий единые пространственно-временные отнош Существует следующие виды интервалов Итак, инвариантами в ИСО являются: скорость света, собственное время и пространственно-временной интервал.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 2. Пространственно-временной интервал как абсолютная характеристика мира событий

Относительность временных и пространственных интервалов.
Понятие пространственно-временного интервала. Абсолютность пространственно-временного интервала по отношению к выбору ИСО.
Времениподобные интервалы. Инвариантные величины в релятивистской механике.



 

Относительность временных и пространственных    интервалов. То, что понятия одновременности удаленных событий не являются инвариантами, следует из преобразований Лоренца. Действительно, выражение для расчета промежутка времени между двумя событиями в системе S', исходя из выражения (15.10), имеет вид:

t' = t₂' - t₁' = ·(t - V·x/c²),     (16.13)
где = (1-^^.

Из уравнения (16.13) следует, что события в системах S и S' являются одновременными (t = 0 и t' = 0) только в одной точке пространства (x = 0). Для удаленных событий понятие одновременности не является абсолютным. Не равны также и величины отрезков r иr' между точками пространства, в которых происходят эти события.

Величины пространственных и временных интервалов не являются абсолютными при описании пространственно-временных отношений, связывающих события в произвольно движущихся ИСО.




Альберт Эйнштейн (1879-1955). Немецкий физик, лауреат Нобелевской премии.

Пространственно-временной интервал. Абсолютность пространственно-временного интервала по отношению к выбору ИСО. Как мы видели в теме 1, величины x, y и z не являются инвариантными по отношению к выбору СО, но их комбинация (длина пространственного отрезка) r является таковой. Попробуем найти комбинацию неинвариантных величинr и t, которая не изменялась бы в произвольной ИСО при любых  скоростях движения.

Рассмотрим частный случай - излучение и прием светового сигнала в системах S и S', начала отсчета которых совпадали в момент испускания сигнала t = t₀ = 0. Из постулата СТО о постоянстве скорости света следует, что

c' =r'/t' = r/t = c.     (16.14)

Таким образом, справедливо соотношение:

c²·(t')² - (r')² = c²·(t)² - (r)² = 0.     (16.15)

В (16.15) мы использовали операцию возведения в квадрат по аналогии с описанием положения частицы в трехмерном пространстве (длина пространственного отрезка равна квадратному корню из суммы квадратов его проекций). Введем величинуI, которую назовем пространственно-временным интервалом, являющуюся комбинацией пространственных и временных характеристик. Пусть квадрат этой величины равен:

I² = c²·(t)² - (r)² = c²·(t)² - (x)² - (y)² - (z)².    (16.16)

В предыдущем примере (для случая событий, связанных световым сигналом) величина  I равнялась нулю. В общем случае, как это можно показать с помощью  преобразований Лоренца, интервал I не равен нулю, но остается постоянным в любой ИСО, т. е. является инвариантом.

Запишем выражение для пространственно-временного интервала ∆I' между двумя произвольными событиями в движущейся СО.

∆I'² = γ·c²·∆t'² -∆x'² - ∆y'² - ∆z'². (16.17)

Используя преобразования Лоренца (15.11) и (15.12), видоизменим уравнение (16.17) через величину пространственно-временного интервала между этими событиями в лабораторной СО. После несложных арифметических преобразований получим, что

∆I'² = γ²·(c² - V²)·∆t² - ∆x²∙ γ²·(1 - V²/ c²) - ∆y² - ∆z² =
= c²·∆t² - ∆x² - ∆y² - ∆z² = ∆I².

Поскольку∆I' = ∆I, то пространственно-временной интервал является инвариантом в любой ИСО.

Эйнштейн ввел новый инвариант I, являющийся комбинацией величин r и t, характеризующий единые пространственно-временные отношения.




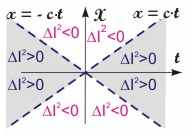
Рис.16.1. Области времени- и пространственноподобных интервалов в двумерном мире событий.

Времениподобные интервалы. Инвариантные величины в релятивистской механике. Пространственный интервал в обычном трехмерном пространстве всегда имеет положительное значение. В мире событий ситуация несколько иная.

Существует следующие виды интервалов:

времениподобные I² > 0 (в величине пространственно временного интервала преобладает временная составляющая, т.е. c²·t² > r²);
светоподобные I² = 0;
пространственноподобные I² < 0 (в величине пространственно временного интервала преобладает пространственная составляющая, т.е. c²·t² < r²).

Графически области расположения этих интервалов в двумерном мире событий приведены на рис. 16.1.

Рассмотрим события, способные влиять друг на друга. Поскольку распространение физического взаимодействия не может осуществляться со скоростями, большими скорости света (см. тему 15), то интервалы I между этими событиями всегда времени- или светоподобны. Действительно, если в какой-либо ИСО события находятся в причинной связи r < c·t, то согласно определению (16.16) I² > 0 и, исходя из инвариантности времениподобного интервала, следует сохранение причинно-следственной связи во всех других ИСО, т.е. r' < c·t'.

Проведем эти рассуждения более детально. Предположим, что в системе S со скоростью  движется частица. За время t она сместится от исходного положения на величину вектора перемещения r = ·t. При этом интервал I будет равен:

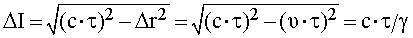.     (16.18)

В собственной СО, движущейся со скоростью V = , частица покоится, следовательно, интервал I' будет равен:

I' = c·₀,     (16.19)
где ₀ - промежуток времени между событиями по часам ССО.

Исходя из инвариантности интервала I' и скорости света из равенства (16.19) следует инвариантность еще одной величины - собственного времени ₀. Связь между собственным временем и временем в произвольной ИСО определяется соотношением:

₀ = /,   (16.20)

т.е. независимо от скорости движения произвольной ИСО, определяющей величину , собственное время одинаково в любой ИСО. Равенство (16.20) доказывает незыблемость причинно-следственных отношений в области  времениподобных интервалов, поскольку знак  определяется знаком ₀ для любых ИСО. Заметим, что хотя величина промежутка времени является относительной, но для времениподобных интервалов понятия "раньше", "позже" абсолютны и определяются инвариантной величиной ₀.

Итак, инвариантами в ИСО являются: скорость света, собственное время и пространственно-временной интервал.