Рис. 14.7. Ламинарное течение жидкости. Фото [13].
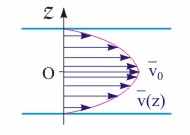
Рис. 14.8. Скорость движения слоев жидкости в горизонтальной трубе при ламинарном течении.
|
Течение реальных жидкостей и газов. Течение вязкой жидкости по трубам в зависимости от ряда условий может быть ламинарным (или слоистым) и турбулентным (или вихревым). В случае ламинарного течения все молекулы жидкости движутся параллельно оси трубы (см. рис. 14.7) и, находясь на одинаковом расстоянии от осевого центра трубы, имеют равные скорости (см. рис. 14.8). Для турбулентного движения характерно наличие нормальной (перпендикулярной направлению течения жидкости) составляющей скорости движения молекул и резкий спад скорости течения при приближении к границам. Траектория движения молекул представляет собой сложную кривую линию (см. рис. 14.9).
Характер течения можно установить, пользуясь безразмерной величиной - числом Рейнольдса:
Re = ·ср·r/h, (14.16)
где - плотность жидкости;
ср - средняя (по сечению трубы) скорость потока;
h - коэффициент вязкости жидкости;
r - характерный геометрический размер,
в частности, радиус сечения цилиндрической трубы.
|

Рис. 14.9. Пример турбулентного течения жидкости.
Фото В. Вестерхолма "Речной порог".
|
Ламинарное течение наблюдается при малых значениях числа Рейнольдса. Начиная с некоторого определенного значения Re, называемого критическим, течение приобретает турбулентный характер. Для воды в гладких круглых трубах Reкр = 2000.
В случае ламинарного течения жидкости согласно третьему закону Ньютона более медленные слои за счет вязкого трения тормозят более быстрые и наоборот, быстрые ускоряют медленные. Причем молекулы стенок трубы не имеют тангенциальной составляющей скорости, и пограничный слой жидкости жестко "прилипает" к ее стенкам. Таким образом, скорость движения отдельных равноудаленных от оси трубы цилиндрических слоев жидкости возрастает от нулевого до максимального значения по мере удаления от стенок трубы (см. рис. 14.8). При стационарном течении распределение скоростей по сечению трубы имеет параболический характер.

|
§ 5. Динамика течения жидкостей и газов Динамика течения жидкостей по трубам. Формула Пуазейля.
Лобовое давление и подъемная сила.
Эффект Магнуса.

|
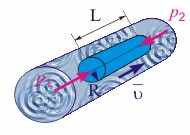
Рис.14.10. К выводу формулы Пуазейля.
|
Формула Пуазейля. Рассмотрим стационарное ламинарное течение жидкости по цилиндрической трубе радиуса R. Пусть жидкость движется под действием перепада давлений p1 и p2 (см. рис. 14.10). Рассчитаем поток или количество жидкости, протекающей через поперечное сечение трубы S в единицу времени. В случае однородного поля скоростей величина потока Q зависит от скорости течения жидкости по следующей формуле:
Q = ·S. (14.17)
Рассчитаем поток жидкости dQ, вытекающей из цилиндрического слоя толщиной dr, расположенного на расстоянии r от оси трубы, а затем проведем интегрирование по всем слоям от 0 до R.
dQ = (r)·dS = (r)·2·r·dr, (14.18)
где dS - площадь поперечного сечения цилиндрического слоя.
Для ответа на поставленный вопрос необходимо найти зависимость (r). Выделим цилиндр радиусом r и длиной L, расположенный симметрично осевой линии трубы (см. рис. 14.10). При стационарном течении скорость течения со временем не изменяется, следовательно, сумма всех сил, действующих на все объемы жидкости, равна нулю. На выделенный цилиндр действуют следующие силы: сила давления, равная произведению разности внешних давлений на площадь поперечного сечения выделенного объема, и сила вязкого трения, действующая на боковую поверхность цилиндра радиусом r, рассчитываемая по формуле Ньютона (14.14). Таким образом,
(p1 - p2)π·r2 = ·|d/dr|·2·r·L. (14.19)
Преобразуя уравнение (14.18), получим, что
- d = (p1 - p2)·r·dr/(2·L). (4.20)
Проинтегрировав выражение (14.20) с учетом граничных условий = 0 при r = R,
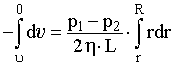 , (14.21) , (14.21)
получим формулу для расчета скорости слоев жидкости, расположенных на расстоянии r от оси трубы:
(r) = (p1 - p2)·(R2 - r2)/(4·L). (14.22)
Максимальная скорость, достигаемая в центре трубы 0, равна:
0 = (p1 - p2)·R2/(4·L). (14.23)
Подставив выражение (14.22) в (14.18) и проведя интегрирование по радиусу, найдем выражение для потока жидкости, вытекающей из трубы:
Q = (p1 - p2)··R4/(2·L). (14.24)
Соотношение (14.24) называется формулой Пуазейля.
Из выражения (14.24) следует, что поток в случае стационарного течения жидкости обусловлен перепадом давлений, зависит от геометрии трубы и свойств жидкости.

|
Жуковский Николай Егорович (1847-1921). Русский ученый в области механики, основоположник современной гидроаэродинамики [12].
|
Лобовое давление и подъемная сила. Рассмотрим движение твердого тела относительно жидкости, находящейся в состоянии покоя в некоторой ИСО. Исходя из принципа относительности эта задача эквивалентна обтеканию неподвижного тела стационарным потоком жидкости.
Силу, действующую на неподвижное тело в направлении потока, называют лобовым сопротивлением, а силу, действующую на него в перпендикулярном направлении, - подъемной силой.
Cтационарное обтекание твердого тела потоком идеальной жидкости не вызывает появления подъемной силы и лобового сопротивления. Покажем это на примере симметричного, покоящегося относительно наблюдателя, тела. В данном случае линии тока относительно вертикальной оси, проходящей через центр масс тела перпендикулярно направлению потока жидкости, симметричны. Следовательно, для симметричных элементарных пространственных областей значения величины скоростей в трубке тока равны по величине. Тогда, исходя из уравнения Бернулли, давления в этих областях попарно равны и лобовое сопротивление отсутствует.
В виду симметрии задачи (но уже по отношению к оси, параллельной потоку) равна нулю и подъемная сила.

|
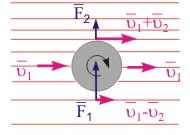
Рис. 14.11. Подъемная сила, действующая на вращающееся тело, помещенное в поток газа.
|
Эффект Магнуса. Иначе дело обстоит для вязкой жидкости или газа. Пусть тело, вращающееся относительно своего центра масс, погружено в газовый поток (см. рис. 14.11). Прилегающие к телу слои молекул участвуют в двух движениях: вращательном, обусловленном наличием вязкого трения между телом и газом, и поступательном, связанным с движением газа вдоль оси трубы. Исходя из векторного закона преобразования скоростей получается картина линий тока, изображенная на рис. 14.11, т. е. скорости потока молекул газа над твердым телом выше, чем под ним. Следовательно, в соответствии с уравнением Бернулли давление над телом будет ниже, чем под ним, и появляется подъемная сила.
Возникновение подъемной силы в результате циркуляции воздуха вокруг твердого тела называется эффектом Магнуса.
|
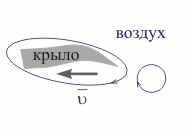
Рис. 14.12. Движение молекул воздуха около крыла самолета.
|
Наиболее характерным примером является наличие подъемной силы у крыла самолета при его движении относительно воздуха. Из-за характерной формы крыла вблизи его острой задней кромки в близлежащих слоях воздуха возникают вихревые воздушные потоки, причем направление вращения молекул происходит против часовой стрелки (см. рис. 14.12). Эти вихревые потоки постепенно нарастают и отрываются от крыла, но за счет наличия вязкого трения они заставляют вращаться по часовой стрелке вокруг поверхности крыла прилегающие к ней молекулы воздуха. Наличие циркуляции, обусловленной вязким трением, и приводит к возникновению подъемной силы.
|







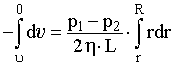 , (14.21)
, (14.21)