1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание Фазочастотная характеристика осциллятора. Резонанс характеризуется наличием максимально благоприятных условий для передачи энергии от источника внешней силы к осциллятору Рассмотрим на качественном уровне физическую картину вынужденных колебаний

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

 


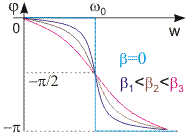
Рис. 13.6. Фазочастотная характеристика

Фазочастотная характеристика осциллятора. Как следует из уравнения (13.12), сдвиг по фазе между силой и смещением зависит от соотношения частот собственной и вынуждающей силы, а также от значения коэффициента затухания β (см. рис. 13.6). При значении w = ω₀ смещение отстает от силы на π/2. Это означает, что в момент, когда сила достигает своего максимального значения, смещение равно нулю, а в момент, когда сила равна нулю - смещение максимально.

С увеличением частоты внешней силы отставание смещения от силы растет и при очень больших частотах w приближается к π, т. е. сила и смещение колеблются в противофазе.

Фазовые соотношения между смещением и внешней силой позволяют более глубоко понять сущность явления резонанса с точки зрения энергетических соображений. Покажем, что при w = ω₀  смещение отстает по фазе от вынуждающей гармонической силы на π/2, т.е. сила и смещение подчиняются следующим законам:

F = F₀·cos (ω₀·t);                
x = A·sin (ω₀·t).    (13.18)

Согласно (13.23) зависимость скорости колеблющейся частицы (осциллятора) от времени имеет вид:

x' = υ = A·ω₀·cos (ω₀·t).    (13.19)

Из соотношений (13.18), (13.19) видно, что скорость и внешняя сила колеблются в фазе. Следовательно, мощность, развиваемая внешней силой, равная N = (F·υ), положительна в любой момент времени. Работа внешней силы в случае w = ω₀ направлена на преодоление сил трения.

При наличии в системе затухания и когда w = ω_р, модуль сдвига фаз между смещением и внешней силой несколько меньше, чем π/2, но мощность, развиваемая внешней силой, не снижается ввиду сопутствующего процесса увеличения значения амплитуды установившихся колебаний осциллятора в резонансе.

Резонанс характеризуется наличием максимально благоприятных условий для передачи энергии от источника внешней силы к осциллятору.

Самые неблагоприятные условия передачи энергии при
w << ω₀ и w >> ω₀. В этих случаях фазы силы и скорости отличаются почти на π. Значит внешняя сила за период колебания осциллятора примерно половину времени направлена противоположно вектору скорости и половину времени совпадает с ней. В среднем осциллятору при этих условиях от источника внешней силы за период колебаний передается незначительная энергия и поэтому их амплитуда очень мала.

Рассмотрим на качественном уровне физическую картину вынужденных колебаний в различных областях частот.

а) w << ₀. В этом случае в закон динамики вынужденных колебаний (13.2) входят слагаемые, пропорциональные ускорению и скорости, много меньше слагаемого ₀²·х, связанного с упругой силой. Следовательно, уравнение движения сводится к следующему виду:

₀²·х = F₀/m · cos(w·t);               
x = F₀·cos(w·t)/k = F(t)/k.     (13.20)

Как вытекает из (13.21), в каждый момент времени смещение является таковым, каким оно должно было бы быть в случае неизменной со временем силы, равной своему мгновенному значению. Силы трения в данном случае себя не проявляют. Смещение совпадает по фазе с внешней силой.

Как вытекает из (13.20) в каждый момент времени смещение является таковым, каким оно должно было бы быть в случае неизменной со временем силы, равной своему мгновенному значению. Силы трения в данном случае себя не проявляют. Смещение совпадает по фазе с внешней силой.

б) w >> ₀. При большой частоте вынуждающей силы слагаемое, обусловленное ускорением, много больше слагаемых, связанных со скоростью и упругой силой. Таким образом, силы упругости и силы трения не играют никакой роли в колебаниях. Внешняя сила действует на осциллятор так, как если бы этих сил не было. Уравнение динамики имеет вид:

x'' = (F₀/m)·cos(w·t).     (13.21)

Решение этого уравнения представляется формулой:

x(t) = -F₀/(m·w^)·cos(w·t) = -F(t)/(m·w^).    (13.22)

Смещение отстает от силы по фазе на .

в) Резонанс. В данном случае система совершает гармонические колебания с частотой w = ₀, следовательно, закон движения можно представить в виде:

 x'' = -ω^·x = 0.

Слагаемое, связанное с ускорением, равно слагаемому, обусловленному упругой силой. Это значит, что ускорение создается силой упругости, а внешняя сила и сила трения взаимно компенсируются. Закон движения (13.2) имеет вид:

2·x' = (F₀/m)·cos(_·t).     (13.23)

Решение уравнения (13.23) представляется формулой:

x = F₀/(2··m·₀)·sin(₀·t).     (13.24)

Смещение отстает от силы по фазе на .




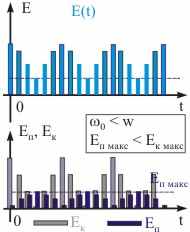
Рис. 13.7. Зависимость энергии установившихся вынужденных колебаний от времени

Энергия установившихся вынужденных колебаний. Энергия установившихся вынужденных колебаний рассчитывается согласно выражению (12.36), но, в отличие от уравнения (12.35) для собственных колебаний, множители перед тригонометрическими функциями не равны:

E = Е_к + Е_п = m·²/2 + k·x²/2 = 
= (m·A²·w²·cos²(w·t + ₀) + k·A²·sin²(w·t + ₀))/2 =
= m·A²·(w²·cos²(w·t + ₀) + ·_²·sin²(w·t + ₀)/2 .    (13.25)

Следовательно, полная механическая энергия установившихся вынужденных колебаний не постоянна. Она изменяется с течением времени по гармоническому закону около некоторого постоянного значения, большего нуля, с частотой, равной 2w (см. рис. 13.7). Амплитуда колебаний полной механической энергии тем меньше, чем ближе частота вынуждающей силы к собственной частоте осциллятора. В случае равенства этих частот полная механическая энергия осциллятора постоянна и равна максимальному значению кинетической или потенциальной энергии:

E = m·A²·_²/2.
где A - амплитуда установившихся вынужденных колебаний.

В общем случае применительно к произвольному моменту времени вклады кинетической и потенциальной энергий в полную механическую энергию осциллятора не равны. Согласно (13.25) в случае w << _ в полной энергии преобладает доля потенциальной, а в случае w >> _ - кинетической энергии.