1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 3. Сложение взаимно перпендикулярных гармонических колебаний. Фигуры Лиссажу

Сложение ортогональных колебаний с равными частотами.
Сложение ортогональных колебаний с кратными частотами.
Фигуры Лиссажу.

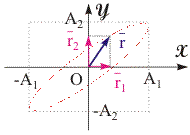Рис. 11.11. Сложение ортогональных колебаний с равными частотами.

Рассмотрим два колебания, описываемых векторными уравнениями: r1 = A1·cos(1·t +1); r2 = A2·cos(2·t +2). Заметим, что с течением времени направление каждого из векторов r1 и r2 не меняется, а изменяются только их величины. Очевидно также, что вектор амплитуды A1 сонаправлен r1, а вектор A2 сонаправлен r2. Найдем уравнение движения частицы, участвующей одновременно в двух описанных выше колебательных процессах, т.е. найдем векторную сумму r = r1 + r2. Рассмотрим частный случай ортогональных (взаимно-перпендикулярных) колебаний (см. рис. 11.11 ). Выберем СО, ось X которой направлена вдоль вектора r1, а ось Y  - вдоль r2. Очевидно, результирующий вектор r в любой момент времени будет находиться в плоскости XY. Фигура, которую описывает конец вектора r вписывается в прямоугольник со сторонами 2A1 и 2A2, а ее вид зависит от соотношения частот, фаз и амплитуд складываемых колебаний. Сложение ортогональных колебаний с равными частотами. Рассмотрим случай ортогональных колебаний с равными частотами: r1 = A1·cos (·t +1);     (11.27) r2 = A2·cos (·t +).     (11.28) Спроецировав уравнения (11.27) и (11.28) на оси координат и проведя суммирование проекций двух колебательных движений, получим: x = A1·cos (·t +1);     (11.29) y = A2·cos (·t +).     (11.30) Исключив с помощью тригонометрических преобразований t из (11.29) и (11.30), получим математическое выражение для траектории движения частицы, которое представляет собой уравнение эллипса: 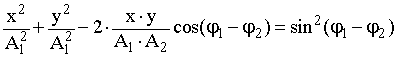. (11.31) Вид эллипса зависит от разности фаз . В общем случае, когда  отлична от 0, полуоси эллипса повернуты относительно осей X и Y на некоторый угол. Если сдвиг фаз  = 0, то, как следует из уравнения (11.31), будет справедливо следующее выражение: (х/А1 - y/A2)2 = 0 или y = А2·x/А1.     (11.32) То есть траектория представляет из себя прямую линию с углом наклона  к оси X, причем tg  = А2/А1. Если  = , то y = - А2·x/А1. Если  = , то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат: х2/А12 + y2/A22 = 1.     (11.33) Если  =  и А1 = А2 = A, то эллипс переходит в окружность радиуса A. х2 + y2 = A2.     (11.34)

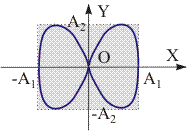Рис. 11.12. Сложение ортогональных колебаний с соотношением частот 1/2. 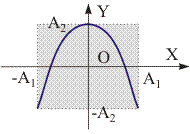      Рис. 11.13. Сложение ортогональных колебаний с соотношением частот 1/2 и разностью фаз /2.

Сложение ортогональных колебаний с кратными частотами. Фигуры Лиссажу. Пусть частоты исходных колебаний 1 и 2 кратны и относятся как целые числа: 1/2 = n1/n2. В данном случае результирующее колебание будет иметь более сложную, чем эллипс, фигуру. Траектории движения частицы, участвующей в ортогональных колебаниях с кратными частотами, называются фигурами Лиссажу. Рассмотрим следующий пример: x = A1·sin·t); y = A2·sin(2·t). (11.35) Для нахождения вида фигуры Лиссажу используем метод графического исключения t. Изобразим на одном графике зависимости x(t) и y(t). Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость XY. В результате получим фигуру Лиссажу типа восьмерки (см. рис. 11.12). Если взять колебания с разными начальными фазами, то при таком же соотношении частот также получим фигуры Лиссажу типа восьмерки, но не симметричные относительно осей координат. При  = , фигура Лиссажу примет вид параболы (см. рис. 11.13). Существует правило частот Лиссажу, согласно которому можно определить отношение частот складываемых колебаний. О величине этого отношения судят по числу точек пересечения фигуры прямыми, параллельными осям координат: y/x = nx/ny.     (11.36) где nx и ny число пересечений фигурой Лиссажу осей X и Y соответственно (или параллельных им прямых). Докажем справедливость правила (11.36). Обозначим за  - минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что  равно наименьшему кратному периодов колебаний Tx и Ty, совершаемых вдоль осей X и Y. За один период конец вектора r пересечет ось X два раза. Следовательно, за время  число пересечений этой оси будет равно  nx = 2·/Ty. Аналогично для числа пересечений оси Y получим, что ny = 2·/Tx. Следовательно,  ny/nx  = Ty/Tx = x/y. Метод фигур Лиссажу широко используется для определения соотношения частот и фаз складываемых колебаний, например, в радиотехнике для градуировки генераторов. Чувствительность фигуры Лиссажу к разности фаз используется также для исследования фазовых соотношений в цепях переменного тока.