1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
 Рис. 10.3. Гироскоп в оправе "карданов подвес". | Гироскоп. Гироскопом называется любое тяжелое симметричное тело, вращающееся вокруг оси симметрии с большой угловой скоростью. Примеры:
Благодаря быстрому вращению, гироскоп имеет уникальные свойства. Рассмотрим их на примере гироскопа в особой оправе, называемой "карданов подвес". Оправа состоит из двух колец: внутреннего и наружного. Непосредственно сам гироскоп представляет собой тяжелое тело в форме диска, способное быстро вращаться с малым трением вокруг его оси симметрии. Ось вращения гироскопа проходит через центр масс и закреплена в подшипниках, расположенных во внутреннем кольце. Внутреннее кольцо может вращаться вокруг горизонтальной оси, опирающейся на подшипники, укрепленные на внешнем кольце. Внешнее кольцо может свободно вращаться вокруг вертикальной оси, проходящей через торцевой подшипник подставки (см. рис.10.3). Силы трения в подшипниках малы. Кольца и диск симметричны относительно своих осей, поэтому гироскоп остается в равновесии в любом положении. В данном случае гироскоп можно рассматривать как симметричное твердое тело, закрепленное в центре масс. Ось гироскопа может занимать любое положение в пространстве. Свободный гироскоп может поворачиваться вокруг трех взаимно перпендикулярных осей, следовательно, он обладает тремя степенями свободы. В случае блокировки поворота вокруг одной из осей (например, вертикальной) гироскоп имеет только две степени свободы и называется несвободным гироскопом.  | ||||||||||
| | Свойства свободного гироскопа. Гироскоп обладает следующими характерными свойствами:
Указанные свойства гироскопа в полной мере проявляются для массивного диска, вращающегося с большой скоростью (критерий этого значения скорости будет приведен в следующем подразделе этого параграфа). При малой скорости вращения вокруг собственной оси гироскоп утрачивает эти свойства. | ||||||||||
| | Элементы физики свободного гироскопа. Неизменность положения оси гироскопа в пространстве объясняется исходя из уравнения моментов, применимого к описанию вращательного движения твердого тела, закрепленного в точке: dL/dt = M. (10.7) На гироскоп действуют сила тяжести и силы реакции со стороны подшипников. Результирующий момент сил реакции подшипников M1 и M2, в которых закреплена ось гироскопа, равен нулю, поскольку подшипники располагаются симметрично относительно СО, связанной с центром масс, а вектора сил F1 и F2, созданных этими силами, равны. Можно показать, что равен нулю и момент однородного поля силы тяжести Mт, в котором находится гироскоп относительно его центра масс. Действительно, Mт = [ri, mi·g] = [mi·ri, g] = [m·rc, g] = 0, где rc - радиус-вектор центра масс гироскопа; ri и mi - радиус-вектор и масса i-й части гироскопа. Итак, мы доказали, что результирующий момент внешних сил равен нулю. Следовательно, в отсутствие сил трения в соответствии с уравнением (10.7) момент импульса гироскопа остается постоянным. Момент импульса величина векторная, и его направление для симметричных тел совпадает с направлением вектора угловой скорости L = I·ω. Таким образом, в отсутствие моментов внешних сил ось гироскопа сохраняет свое положение относительно ИСО. При ударных воздействиях на одну из оправ гироскопа момент, создаваемый конечной по величине внешней силой, вызывает пренебрежительно малое изменение величины момента импульса L = M·t ( L/L << 1). Следовательно, направление оси гироскопа, совпадающее с вектором L при быстром вращении, за время удара не успевает измениться.  | ||||||||||
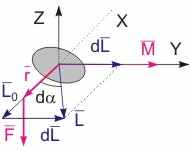 Рис. 10.4. Необычная реакция гироскопа на действие внешней силы. | Рассмотрим движение гироскопа под действием постоянно действующего момента внешней силы (см. рис. 10.7). Пусть начальный момент импульса гироскопа L0 направлен вдоль оси X. Пусть к оси (соответствующему кольцу "карданова подвеса") приложена сила F, направлен вдоль вертикальной оси Z. Момент этой силы, равный векторному произведению [r, F], сориентирован вдоль горизонтальной оси Y. В данном направлении согласно основному закону динамики вращательного движения сориентирован также и вектор элементарного приращения момента импульса dL. Таким образом, по истечении времени dt момент импульса L изменит свое направление в пространстве, повернувшись на некоторый угол d вокруг оси Z: L = L0 + dL. (10.8) Покажем, что ось гироскопа при быстром его вращении повернется вокруг оси Z на такой же угол. Действительно, диск гироскопа участвует в двух движениях: быстром вращении вокруг своей оси и медленном, связанном с поворотом этой оси. Таким образом, ось симметрии гироскопа не совпадает по направлению с мгновенной осью вращения и, следовательно направлением вектора момента импульса. Однако при большой скорости вращения гироскопа (малом отношении dL/L) этим различием можно пренебречь и считать, что вектор момента импульса сориентирован вдоль оси симметрии гироскопа и движется вместе с ней. Ось гироскопа перемещается в направлении действия момента силы, а не самой силы, что и обуславливает необычную реакцию гироскопа на его воздействие. Гироскоп в соответствии с законом (10.7) безынерционен. Как только мы уберем внешнее воздействие, вращение в направлении действия момента силы прекратится (однако сам гироскоп будет продолжать вращаться).  | ||||||||||
 Рис. 10.5. Прецессия гироскопа.  Рис. 10.6. К расчету скорости прецессии. | Прецессия. Прецессией гироскопа называется движение по окружности конца оси гироскопа относительно некоторой оси, сориентированной вдоль вектора внешней силы, происходящее под действием этой силы (см. рис.10.5). Вычислим угловую скорость прецессии гироскопа п, ось которого смещена относительно горизонтальной плоскости на угол (см. рис. 10.6). Прецессия обусловлена действием внешней силы F, создающей момент M. п = d/dt; d = dL/(L·cos()) = M·dt/(L·cos()); п = M/(L·cos()) = M/(I··cos()), (10.9) где L·cos() - проекция момента импульса на плоскость вращения гироскопа (плоскость, в которой располагаются вектора dL). Скорость прецессии гироскопа определяется величиной внешней силы F, точкой ее приложения, угловой скоростью вращения диска гироскопа и его моментом инерции I. Направление прецессии зависит от направления действующей силы и направления вращения диска. Пример. Прецессия волчка (см. рис. 10.5). В качестве внешней силы на волчок действует сила тяжести m·g, приложенная к его центру масс. Волчок вращается вокруг оси, составляющей некоторый угол с вертикалью. Скорость прецессии равна: п = M/(L·sin()) = m·g·l·sin()/(L·sin()) = m·g·l/(I·), (10.10) где l - расстояние от точки вращения до центра масс, - угол между направлением действия силы тяжести и моментом импульса волчка.  | ||||||||||
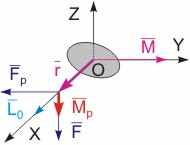 Рис. 10.7. Свойство несвободного гироскопа №1. | Несвободный гироскоп. Гироскопические эффекты. Если закрепить одно из колец "карданова подвеса", то соответствующая вращательная степень свободы исчезнет. Мы получим гироскоп с двумя степенями свободы. Его свойства совершенно другие. При вращении гироскопа относительно одной из осей он не будет "сопротивляться", т.е. будет вести себя как обычный диск, одна из осей которого закреплена в подшипниках кольца. Пусть на ось OX гироскопа действует сила F, направленная против оси OZ (см. рис. 10.7). Момент этой силы направлен вдоль оси OY. Данный момент стремится повернуть гироскоп относительно оси OZ, чему препятствуют силы реакции Fp (пара сил), возникающие в подшипниках, в которых закреплена ось гироскопа. Силы Fp называются гироскопическими силами. Их появление обусловлено тем, что наружное кольцо жестко закреплено и не может вращаться относительно вертикальной оси. Гироскопические силы создадут гироскопический момент Mp, сонаправленный вектору F. В этом направлении и будет происходить изменение момента импульса. Несвободный гироскоп, таким образом, является "послушным". Возникновение гироскопических сил в различных устройствах и системах называется гироскопическим эффектом. К отрицательным последствиям проявления этих эффектов можно отнести разрушение механических конструкций, содержащих массивные вращающиеся детали. Гироскопические силы возникают в подшипниках при попытке изменения положения осей различных механических узлов, приведенных во вращение. Например, в турбинах, колесах автомобилей, пропеллерах самолетов и т.д. | ||||||||||
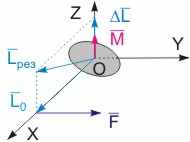 Рис. 10.8. Свойство несвободного гироскопа №2. | Рассмотрим теперь результат поворота вокруг вертикальной оси закрепленного наружного кольца гироскопа (см. рис. 10.8). В этом случае ось гироскопа будет поворачиваться вокруг горизонтальной оси до тех пор, пока его момент импульса не совпадет по направлению с вектором угловой скорости оправы. Действительно, при вращении вокруг вертикальной оси гироскопу передается момент сил, направленный вдоль оси вращения наружного кольца (см. рис. 10.8). Этот момент будет вызывать вращение гироскопа вокруг горизонтальной оси до тех пор, пока направления векторов изменения момента импульса L (момента сил) и момента импульса гироскопа L не совпадут.  | ||||||||||
| | Применение гироскопов. Гироскопы применяются в различных технических устройствах. Приведем лишь несколько примеров их использования.
|


