1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 1. Динамика поступательного движения твердого тела Об эквивалентности описания движения частицы и поступательного движения твердого тела. Уравнение динамики поступательного движения твердого тела.
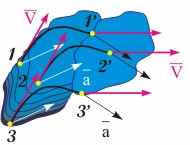Рис. 9.1. Поступательное движение твердого тела (без штрихов - начальное положение произвольных точек тела, со штрихами - их конечное положение)	Уравнение поступательного движения твердого тела. Разобьем абсолютно твердое тело на элементарные части, обладающие массами mi, которые можно считать материальными точками. Так как в случае поступательного движения все элементарные массы твердого тела движутся с одинаковыми скоростями и ускорениями (см. рис. 9.1), то для каждой из них справедлив второй закон Ньютона: 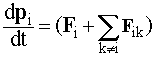,     (9.1) где Fi - равнодействующая внешних сил, приложенных к элементарной массе mi; Fik - сила взаимодействия между i-й и k-й частями тела.   Просуммировав уравнения (9.1) по индексу i, получим выражение для расчета скорости изменения импульса абсолютно твердого тела dp/dt: 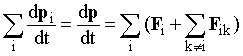.  (9.2) Поскольку согласно третьему закону Ньютона сумма всех внутренних сил системы равняется нулю, то исходя из уравнения (9.2), получим закон динамики поступательного движения твердого тела: 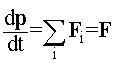.   (9.3) где F - результирующая внешних сил, действующих на тело. Уравнение (9.3) в точности повторяет уравнение движения центра масс системы. Следовательно, поступательное движение твердого тела можно рассматривать как движение материальной точки массой, равной массе твердого тела, происходящее под действием внешних сил, приложенных к нему.
§ 2. Элементы статики. Основное уравнение динамики вращательного движения Понятие момента силы относительно произвольной точки. Момент силы относительно закрепленной оси. Момент инерции. Теорема Штейнера. Основной закон динамики твердого тела. Условия равновесия твердого тела. Момент пары сил.
Рис. 9.2. Маятник Обербека	Рассмотрим движение твердого тела вокруг закрепленной оси с точки зрения анализа причин этого движения и выявим физические характеристики, необходимые для его описания. В качестве примера рассмотрим вращение симметричной крестовины с закрепленными на ней грузами, положение которых можем изменять. Крестовину укрепим в подшипнике, насаженном на неподвижной оси - металлическом стержне. На ось насадим также второй подшипник с катушкой и намотаем на нее нить (нить можно наматывать на различные части катушки, отличающиеся диаметром). Свободный конец нити перекинем через блок и подвесим к ней груз. Описанная выше конструкция называется маятником Обербека (см. рис. 9.2). Если крестовину отпустить, то благодаря действию силы притяжения груз начнет двигаться поступательно по направлению к Земле, а подшипники и связанные с ними крестовина и катушка придут во вращение вокруг закрепленной оси. Результаты эксперимента, полученные с помощью маятника Обербека, свидетельствуют о том, что угловое ускорение твердого тела, вызванное внешними силами, зависит:  - не только от массы твердого тела (крестовины), но и от ее распределения относительно оси вращения, - не только от внешней силы, но и от точки ее приложения. Таким образом, для количественного описания вращательного движения твердого тела необходимо ввести дополнительные (по отношению к описанию поступательного движения) характеристики, адекватно соотносящиеся с результатами эксперимента.
Рис. 9.3. К понятию момента силы, действующей на материальную точку	Момент силы относительно произвольной точки. Пусть частица A движется относительно точки О под действием произвольной  силы F (см. рис. 9.3). Моментом силы M относительно произвольной точки О называется векторное произведение радиус-вектора частицы r, проведенного из точки O в точку приложения силы, на вектор силы F: M = [r, F].     (9.4)
Рис. 9.4. Определение направления момента силы	Момент силы перпендикулярен плоскости, в которой находятся вектора r и F. Направление вектора M задается правилом векторного произведения. Вектора r и F изображают исходящими из одной точки и связывают с ними правый винт (см. рис. 9.4). Затем головку винта поворачивают по кратчайшему пути от вектора r к F. Поступательное движение винта происходит сонаправленно вектору M. Величина вектора момента сил рассчитывается согласно уравнению (9.5): M = r·F·sin() = F·R,     (9.5) где R = r·sin() - плечо силы, равное кратчайшему расстоянию  от оси вращения до линии действия силы (см. рис. 9.2).
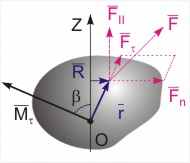Рис. 9.5. К определению момента силы относительно закрепленной оси	Момент силы относительно закрепленной оси. Моментом силы относительно произвольной оси Z называется величина, равная проекции вектора момента сил M на данную ось, взятого относительно произвольной точки O, расположенной на этой оси (см. рис. 9.5). Mz = [r, F]z .    (9.6) Найдем значение вектора M для твердого тела, вращающегося вокруг закрепленной оси Z под действием силы F. Разложим эту силу на три составляющие (см. рис.9.5): F = F|| + F + Fn, где F|| - составляющая силы, параллельная оси вращения; F - тангенциальная составляющая силы, расположенная в плоскости вращения; Fn - нормальная составляющая силы, расположенная в плоскости вращения. Момент силы относительно точки О можно представить как векторную сумму соответствующих моментов, созданных этими силами: M = M|| + M + Mn.
Иллюстрация понятия момент силы. Неподвижная ось - это голень. Чем дальше рука спортсмена относительно оси, тем легче сломать ракетку. Аугусто Куэртен. Сидней, Олимпийские игры 2001 г.  AP and Renters	Моменты M|| и Mn перпендикулярны оси вращения, и их проекции на эту ось равны нулю. Момент силы Mобразует с ней угол . Таким образом, проекция результирующего момента на ось Z равна (см. рис.9.5): Mz = Mz = |M|·cos(=r·F·cos(= R·F.     (9.7) Как видно из уравнения (9.7), величина момента силы относительно закрепленной оси не зависит от выбора точки O на этой оси. Из опыта следует, что только сила F способна вызвать вращение тела вокруг закрепленной оси, причем чем дальше от оси расположена точка приложения тангенциальной составляющей силы, тем легче осуществить поворот вокруг этой оси. Следовательно, момент силы относительно оси характеризует способность силы вращать тело относительно данной оси. Из последнего утверждения вытекает условие равновесия твердого тела относительно закрепленной оси. Если сумма моментов внешних сил относительно закрепленной оси равна нулю, то тело находится в положении равновесия относительно этой оси.
	Момент инерции. Моментом инерции материальной точки массой m относительно оси вращения называется величина, равная: I = m·R2,      (9.8) где R - кратчайшее расстояние от оси вращения до точки. Момент инерции системы материальных точек равен сумме моментов инерции его частей: I = mi·Ri2.      (9.9) Момент инерции твердого тела равен сумме моментов инерций его частей и рассчитывается путем интегрирования по всему телу: .    (9.10) Следовательно, момент инерции твердого тела зависит от: массы тела; формы и размеров тела; распределения массы относительно оси вращения. Для симметричных однородных тел моменты инерции рассчитываются с помощью элементарного интегрального исчисления. Формулы для расчета моментов инерции некоторых из них приведены в таблице.
	Теорема Штейнера. При переносе оси вращения или отдельных частей тела относительно этой оси его момент инерции изменяется. Соотношение между моментами инерции тела относительно некоторой оси вращения, проходящей через центр масс, и относительно произвольной, параллельной ей оси устанавливается с помощью теоремы Штейнера (ГюйгенсаШтейнера). Проведем некоторую ось вращения Z, проходящую через центр масс твердого тела. Выберем другую произвольную ось Z', параллельную оси Z. Момент инерции относительно оси Z равен: I0 = Σmi·Rci2, где Rci - расстояние от частей твердого тела до центра масс. Момент инерции относительно оси  Z' рассчитаем аналогичным образом. I = Σmi·Ri2, где Ri - кратчайшее расстояние от частей твердого тела до точки пересечения с осью Z'. Воспользовавшись выражением для преобразования координат при переходе между СО, получим, что I = Σmi·Ri2 = Σmi·(d + Rci)2 = = Σmi·d2 + Σmi·Rci2 + 2Σmi·(d, Rci) = = d2·Σmi + Σmi·Rci2 + 2(d, Σmi·Rci),    (9.11) где d - кратчайшее расстояние между осями. Исходя из определения центра масс последнее слагаемое в уравнении (9.11) равняется нулю. Следовательно, момент инерции I можно рассчитать как: I = I0 + m·d2,   (9.12) где m = Σmi - масса твердого тела. Уравнение (9.12) является аналитическим выражением теоремы Штейнера. Момент инерции тела относительно произвольной оси вращения равен сумме момента инерции этого тела, взятого относительно параллельной ей оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями.
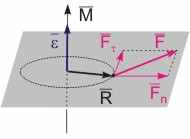Рис. 9.6. К выводу основного уравнения динамики вращательного движения	Уравнение динамики вращательного движения материальной точки. Рассмотрим изменение характера движения частицы массой m, вращающейся вокруг точки О по окружности радиуса R, за счет действия результирующей внешней силы F (см. рис. 9.6). В инерциальной системе отсчета справедлив второй закон Ньютона. Запишем его применительно к произвольному моменту времени: F = m·a. Мы знаем, что нормальная составляющая силы не способна изменить характер вращательного движения частицы, поэтому рассмотрим действие только тангенциальной составляющей силы. В проекции на тангенциальное направление уравнение движения частицы примет вид: F= m·a.    (9.13) Поскольку  a = ·R, то F= m··R(9.14) Умножив левую и правую части уравнения (9.14) на R, получим: F·R= m··R2     (9.15) Mz = I·    (9.16) Уравнение (9.16) описывает вращательное движение материальной точки, исходя из представления динамики. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление сонаправленного ему вектора углового ускорения, который параллельна оси вращения (см. рис. 9.6): M = I·     (9.17) Выражение (9.17) представляет собой основной закон динамики вращательного движения материальной точки: произведение момента инерции частицы на ее угловое ускорение равно результирующему моменту сил, действующих на эту частицу.
F --- M m --- I a ---  F = m·a --- M = I·	Закон динамики вращательного движения твердого тела. Обобщим полученный результат для твердого тела, закрепленного в точке O (например, стержень, один из концов которого закреплен в шаровом подшипнике).  Разобьем тело на элементарные участки массой mi. Пусть Ri - кратчайшее расстояние от оси, относительно которой происходит вращение, до элемента массой mi, а Ii - его момент инерции относительно этой оси. Обозначим за Mi результирующий момент внешних сил, действующий на элемент mi, а Mi* - результирующий момент внутренних сил, действующий на него со стороны других элементов тела. Из уравнения (9.17) следует, что: Mi + Mi* = Ii·(9.18) Просуммировав уравнение (9.18) по всем элементам и учитывая, что согласно третьему закону Ньютона результирующий момент внутренних сил равен нулю, получим уравнение, аналогичное (9.17), задающее движение частицы: M = I·(9.19) где M - результирующий момент внешних сил, действующих на твердое тело,  относительно точки О; I - момент инерции тела относительно оси вращения. Основной закон динамики вращательного движения твердого тела относительно закрепленной точки можно сформулировать следующим образом: произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение. Момент силы M относительно точки O, в которой закреплено тело, характеризует способность силы вращать тело вокруг этой точки. Причем его поворот произойдет вокруг оси, параллельной вектору результирующего момента внешних сил M, взятому относительно точки O. Итак, при вращательном движении твердого тела относительно закрепленной точки результат силового воздействия характеризуется величиной и направлением вектора момента силы. Для описания движения твердого тела относительно закрепленной оси необходимо спроецировать уравнение (9.19) на эту ось: Mz = Iz·.     (9.20) Из уравнения (9.20) можно найти величину углового ускорения относительно закрепленной оси. Твердое тело приобретет угловое ускорение относительно закрепленной оси под действием проекции момента сил Mz. На основании основного закона динамики вращательного движения в проекции на ось вращения можно доказать теорему об изменении кинетической энергии для вращающегося тела. Действительно, dA = Mz·d= I··d = I·(d/dt)··dt = I·d(2/2), где Mz - проекция результирующего момента всех сил, действующих на тело. Произведя интегрирование по углу, получим:  A12 = I·22/2 - I·12/2 = Eк.
Условия равновесия. Фото andre@andre.ru 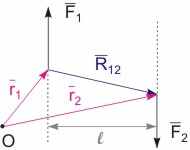  Рис. 9.7. К расчету момента пары сил	Условия равновесия твердого тела. Тело находится в равновесии относительно выбранной ИСО, если оно не обладает ускорением поступательного и вращательного движений, т. е. выполняются следующие условия: a = 0,  = 0. Очевидно, что это имеет место при равенстве нулю результирующей внешних сил F и результирующего момента внешних сил M, действующих на тело. Условие равновесия твердого тела заключается в выполнении векторных соотношений (9.21): F = 0 и M = 0.     (9.21) Заметим, что равенство нулю результирующего вектора сил не обязательно обуславливает равенство нулю результирующего момента внешних сил, действующих на тело. Типичным примером такого рода является действие момента пары сил  F1 = -F2 (см. рис. 9.7), вызывающего движение тела с угловым ускорением. Расстояние между линиями продолжения сил l называется плечом пары. Момент пары сил равен: M = [r1, F1] + [r2, F2]= -[R12, F1], где R12 - вектор, соединяющий точки приложения сил. Величина вектора момента пары сил в отличие от величины вектора результирующей внешней силы не равняется нулю. |M| = l·F1.     (9.22)