1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 3. Момент импульса. Уравнение моментов

Понятие момента импульса частицы.
Момент импульса твердого тела.
Вектор момента импульса симметричных тел.
Уравнение моментов.

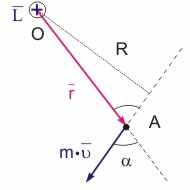
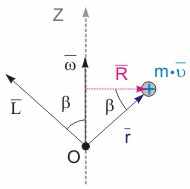
Рис. 9.8. К определению момента импульса частицы, движущейся относительно произвольной точки O         Рис. 9.9. К определению момента импульса частицы, вращающейся вокруг закрепленной оси	Момент импульса частицы. Моментом импульса L частицы A относительно точки О называется величина, равная векторному произведению радиус-вектора частицы r на ее импульс p:  L = [r, p] = m·[r, ].    (9.23) В общем случае произвольного движения частицы относительно точки О модуль момента импульса частицы равен:  L = r·m··sin() = R·m·,    (9.24) где R - плечо импульса частицы относительно точки О (см. рис. 9.8). Пусть частица массой m совершает вращательное движение вокруг некоторой произвольной оси Z с угловой скоростью  (см. рис. 9.9). Направление вектора момента импульса относительно произвольной точки О, расположенной на этой оси, как следует из рис. 9.9, составляет с ней угол  и не совпадает с направлением вектора угловой скорости. Учитывая, что вектора r и  взаимно перпендикулярны, получим выражение для расчета величины вектора момента импульса частицы относительно точки О:  L = r·m·.    (9.25) Моментом импульса Lz частицы относительно произвольной оси Z называется проекция вектора L на эту ось. Как видно из рис. 9.10,  Lz = L·cos () = R·m·.    (9.26) Как следует из выражения (9.26), момент импульса частицы относительно закрепленной оси не зависит от выбора точки O на этой оси.
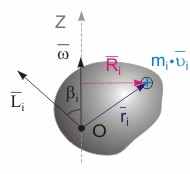
Рис. 9.10. К определению момента импульса твердого тела, вращающегося относительно закрепленной оси                       --- m --- I p --- L p = m· --- L = I·	Момент импульса твердого тела. Рассмотрим твердое тело, совершающее вращательное движение вокруг некоторой закрепленной оси с угловой скоростью . Моментом импульса тела называется величина, равная векторной сумме моментов импульса его частей:  L = Li = [ri, pi] = mi·[ri i].    (9.27) Очевидно, что, как и для случая с частицей, проекция момента импульса i-й части тела на ось Z в соответствие с рис. 9.10 равна: Lzi = Ri·mi·i = Ri2·mi·z.    (9.28) Произведя суммирование по всему телу и исходя из определения момента инерции, получим выражение для расчета проекции момента импульса тела на ось Z: Lz = Lzi = Li·cos (i) = Ri2·mi·z = Iz·z.    (9.29) При суммировании мы учли, что значения проекций векторов моментов импульса каждой части тела на ось Z имеют одинаковые знаки, т.к. для них (как следует из геометрических соображений) углы между вектором угловой скорости и моментами импульсов всегда острые. Заметим, что выражение (9.29) не зависит от выбора точки О на оси вращения. В случае симметричного тела и нахождения точки О на оси симметрии направление момента импульса тела совпадает с направлением его угловой скорости, т. к. всегда найдется пара симметричных точек, для которых составляющие вектора L, расположенные в плоскости вращения, скомпенсированы. Следовательно, для симметричного тела, вращающегося вокруг оси симметрии, справедливо векторное равенство: L = I·.    (9.30) Момент импульса симметричного тела, вращающегося вокруг оси симметрии, равен произведению его момента инерции относительно этой оси на угловую скорость. В случае несимметричного тела результирующий вектор L направлен под произвольным углом к оси вращения и конец вектора L совершает вокруг нее вращательное движение (прецессирует). Заметим, что уравнение (9.30) аналогично выражению для импульса твердого тела в случае его поступательного движения p = m·. Следовательно,  момент импульса твердого тела есть его характеристика при вращательном движении.
F = dp/dt --- M = dL/dt	Уравнение моментов. Пользуясь уравнением (9.27), найдем скорость изменения момента импульса тела: dL/dt = ([dri/dt, pi] + [ri, dpi/dt]).    (9.31) Первое слагаемое в правой части выражения (9.31) равняется нулю, поскольку производная от радиуса по времени, представляющая собой скорость i-й части тела, сонаправленной ее импульсу. Другое слагаемое преобразуем, воспользовавшись вторым законом Ньютона: dpi/dt = Fi + Fi*,    (9.32) где Fi и Fi* - соответственно равнодействующие внешних и внутренних сил, действующих на i-й элемент тела. Подставив выражение (9.32) в (9.31), получим, что скорость изменения момента импульса равняется сумме моментов внешних Mi и внутренних Mi* сил. Поскольку последний из них равен нулю, то dL/dt = (Mi + Mi*) = Mi = M.    (9.33) Скорость изменения момента импульса вращающегося тела равняется векторной сумме моментов внешних сил, действующих на него. Уравнение (9.33) называется уравнением динамики вращательного движения в форме моментов или уравнением моментов.