Geum.ru

1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материалаДокументы

Содержание


§ 1. Законы изменения и сохранения момента импульса системы
Закон изменения момента импульса.
Следствия из закон сохранения момента импульса
Примеры:к первому следствию
Сохранение момента импульса и изотропность пространства.
Подобный материал:
1   ...   14   15   16   17   18   19   20   21   ...   35



§ 1. Законы изменения и сохранения момента импульса системы
Закон изменения момента импульса.
Закон сохранения момента импульса.
Следствия закона сохранения момента импульса.
Изотропность пространства и закон сохранения момента импульса.

 
Закон изменения момента импульса. Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей Li, взятых относительно одной и той же точки выбранной системы отсчета.

L = ΣLi.     (10.1)

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела (9.31)(9.33), получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

dL/dt = M.     (10.2)

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (10.2) представляет собой закон изменения момента импульса системы. Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением 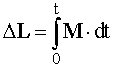(10.3.

.     (10.3)

Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее.

Уравнения (10.2) и (10.3) справедливы как в ИСО, так и в НСО. В неинерциальной СО к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.
 



Рис. 10.1. Следствие закона сохранения момента импульса. Величина вектора угловой скорости скамьи на верхнем фрагменте фотографии меньше, чем на нижнем.
Закон сохранения момента импульса. Из закона изменения момента импульса, полученного нами для системы тел, вытекает закон сохранения момента импульса применительно к механике:

момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Еще раз подчеркнем, что при использовании этого закона моменты импульса и сил необходимо брать относительно одно и той же оси.

Закон сохранения момента импульса является фундаментальным законом природы и выполняется для любых, а не только механических систем.

Следствия из закон сохранения момента импульса:



в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;



если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;



в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.

Примеры:
к первому следствию - при движении человека, находящегося на поверхности диска, по окружности с центром, совпадающим с центром масс диска, последний начинает поворачиваться в сторону, противоположную движению человека относительно Земли; 
ко второму следствию - ко второму следствию - студент, держащий в вытянутых расправленных руках гантели, сидит на скамье (скамье Жуковского), которая вращается вокруг вертикальной оси  (см. рис. 10.1). В случае приближения гантелей к груди угловая скорость движения системы “скамья-студент-гантели” увеличивается.



Рис. 10.2. Пример выполнения закона сохранения момента импульса. При изменении положения оси вращающегося колеса студентом неподвижная изначально скамья приходит во вращение.
к третьему следствию к третьему следствию (см. рис. 10.2) - в начальный момент времени студент сидит на неподвижной скамье Жуковского и удерживает в руках раскрученное колесо. Пусть ось вращения колеса перпендикулярна оси вращения Z скамьи Жуковского, т. е. расположена в горизонтальной плоскости. При повороте колеса на 90о в вертикальной плоскости проекция момента импульса системы “скамья-студент-колесо” на вертикальную ось Lz не изменится и останется равной нулю.

Lz = Lz студ + Lz кол = Lz0 = 0, т.е. Lz студ = - Lz кол.

Следовательно, вектора угловых скоростей системы “студент-скамья” и колеса направлены в противоположные стороны.

 
Сохранение момента импульса и изотропность пространства. Изотропность пространства обусловлена симметрией пространства к операции поворота (см. § 2 темы 1). В случае поворота замкнутой системы на угол  относительно выбранной ИСО работу могут совершить только внутренние силы. При этом работа консервативных сил, зависящая исключительно от изменения взаимного расположения частей системы, равняется нулю. Неконсервативные силы ввиду отсутствия относительного движения частей системы работы не совершают. Следовательно, работа всех внутренних сил системы равня-ется нулю.

dA1-2 = Σ(M*i, dα) = 0.     (10.4)

Из уравнения (10.4) вытекает, что результирующий момент внутренних сил в замкнутой системе отсчета также равен нулю

M = ΣM*i = 0.     (10.5)

В соответствии с законом динамики вращательного движения и уравнением (10.5) момент импульса замкнутой системы при осуществлении операции ее поворота сохраняется.

L = M/dt = M*/dt = 0.     (10.6)

Таким образом, соблюдение условия (10.4) позволяет получить закон сохранения момента импульса замкнутой системы, используя для этого вместо третьего закона Ньютона одно из свойств симметрии пространства - его изотропность.