1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 3. Колебания под действием внешней негармонической периодической силы

Уравнение динамики вынужденных колебаний под действием негармонической периодической силы.
Решение уравнения динамики вынужденных колебаний.
Гармонический анализ.

Рис. 13.8. Амплитудочастотный спектр	Уравнение динамики вынужденных колебаний под действием негармонической периодической силы. Пусть на гармонический осциллятор действует негармоническая периодическая внешняя сила: F(t) = F(t + n·T),     (13.26) где Т - период внешней силы. По известным из математического анализа формулам ее можно представить в виде ряда Фурье, каждое слагаемое которого является гармонической функцией: F(t) = F0i·cos(wi·t + i),     (13.27) где wi = i·wc = n·2·/T;  i = 1, 2, 3,..., n; wc - частота самой низкой гармоники (основная частота),  равная частоте вынуждающей силы w, wc = w1 = w = 2/T. Набор wi называется частотным спектром силы, набор Foi называется амплитудным спектром силы, а набор i - фазовым спектром силы. Силу принято изображать в виде диаграммы амплитудочастотного спектра (см. рис. 13.8). Рассмотрим действие, которое оказывает на осциллятор внешняя негармоническая периодическая сила вида (13.27). Закон динамики осциллятора в этом случае выглядит следующим образом: x'' + 2··x' + 02·x = F0i·cos(wi·t + i)/m.     (13.28) Решение уравнения динамики вынужденных колебаний. Как следует из теории дифференциальных уравнений, для решения уравнения (13.28) дополнительных расчетов не требуется. Достаточно учесть, что оно является линейным и, следовательно, его решение может быть представлено как сумма решений уравнений, в правой части каждого из которых стоит только одно из слагаемых суммы (13.28). Другими словами, каждая из составляющих амплитудного спектра сил действует на осциллятор независимо, причем, результат такого действия нам известен из анализа колебаний под действием гармонической внешней силы (13.5).
принцип суперпозиции	Следовательно, результирующее колебание представляет собой алгебраическую сумму величин xi(t), вызываемых отдельными гармониками силы Fi, что соответствует принципу суперпозиции силового действия. Результирующее колебание рассчитывается по формуле:  x(t) = xi(t).
	Подчеркнем, что принцип суперпозиции справедлив только для линейных явлений. В данном случае в системах возможно протекание сразу нескольких независимых колебательных процессов, которые не оказывают никакого влияния друг на друга. Для нелинейных явлений отклик системы не пропорционален оказанному воздействию и колебательные процессы начинают влиять друг на друга. Например, одновременное возбуждение в нелинейной системе двух колебаний с разными частотами приводит к возникновению составляющих результирующего колебания на кратных, суммарных и разностных частотах. Можно отметить следующие закономерности колебаний, происходящих под действием внешней негармонической периодической силы: каждая составляющая негармонической периодической внешней силы вызывает гармоническое колебание с периодом этой составляющей; гармонический осциллятор с одной степенью свободы под действием внешней негармонической периодической силы совершает негармоническое колебание с периодом, равным периоду этой силы. Результирующее колебание представляет собой сумму гармонических колебаний; амплитуды отдельных гармоник установившихся вынужденных колебаний Аi зависят от соотношения между частотой гармонической составляющей внешней силы и собственной частоты системы; форма x(t) не совпадает с формой F(t).
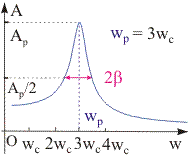Рис. 13.9. Амплитудочастотная характеристика, соответствующая действию на осциллятор негармонической периодической внешней силы (амплитудно-частотный спектр этого осциллятора приведен на рис. 13.8)	Гармонический анализ. Рассмотрим еще один вопрос. Может ли негармоническая сила вызвать гармонические колебания системы? На рис. 13.9 изображена амплитудочастотная характеристика (АЧХ), соответствующая воздействию на систему негармонической периодической внешней силы с амплитудочастотным спектром, приведенным на рис. 13.8. Очевидно, что в нашем примере третья гармоника вызывает колебания с наибольшей амплитудой, т.к. она соответствует возбуждению колебаний в режиме резонанса. Ее частота 3·wс = wр. Остальные гармоники практически не вызовут колебаний, т. к. их частоты далеки от резонансной, и амплитуды вызываемых ими колебаний очень малы. Следовательно, осциллятор с острой резонансной кривой может колебаться гармонически в ответ на действие внешней негармонической периодической силы. Такая система селективно (выборочно) откликается на внешнее воздействие, только на ту составляющую, частота которой близка к собственной частоте системы. Изменяя собственную частоту системы можно произвести разложение внешней силы в ряд по гармоническим составляющим (сделать анализ спектра внешней силы). Эта операция называется гармоническим анализом.