1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 1. Динамика вынужденных колебаний под действием гармонической силы Понятие вынужденных колебаний. Закон динамики вынужденных колебаний, происходящих под действием гармонической силы. Уравнение вынужденных колебаний. Переходный и установившийся режимы вынужденных колебаний. Расчет амплитуды и фазы установившихся вынужденных колебаний.
Пример вынужденных колебаний [11]	Закон динамики колебаний, происходящих  под действием гармонической силы. Рассмотрим движение частицы, происходящее под действием внешней переменной (по направлению) силы. Из интуитивных соображений понятно, что такого рода движение будет колебательным (в частном случае - периодическим). Вынужденными называются колебания, которые совершает физическая система под действием переменной внешней силы. Характер движения зависит от особенностей этой силы.  Наиболее важным является случай гармонического внешнего воздействия. Более сложные случаи его изменения во времени сводятся к этому простейшему. Будем считать, что на осциллятор действует гармоническая внешняя сила, изменяющаяся по следующему закону: F = F0·cos(w·t).     (13.1) где w и F0 - частота и амплитуда внешней силы. Кроме внешней силы на осциллятор как и в случае собственных колебаний действуют квазиупругая сила и сила трения. Согласно второму закону Ньютона движение осциллятора описывается следующим уравнением: m·x'' + h·x' + k·x = F0·cos(w·t). После проведения преобразований получим закон движения для вынужденных колебаний под действием гармонической силы: x'' + 2··x' + 02·x = F0·cos(w·t)/m.     (13.2)
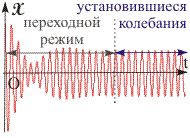Рис. 13.1. График вынужденных колебаний w > 0	Уравнение вынужденных колебаний. Закон движения (13.2) представляет собой линейное неоднородное дифференциальное уравнение второго порядка. Напомним, что в неоднородном уравнении, в отличие от однородного, существуют слагаемые, содержащие аргумент в явном виде (в нашем случае - время t). Общее решение x(t) неоднородного дифференциального уравнения (решение, справедливое при любых значениях входящих в него параметров)  представляет собой сумму общего решения однородного уравнения x1(t) и частного решения неоднородного уравнения x2(t), т. е.   x(t) = x1(t) + x2(t).     (13.3) Частным решением дифференциального уравнения называется такое решение, которое справедливо только при строго определенных значениях входящих в него параметров. Первое из этих слагаемых нам известно - это уравнения собственных затухающих колебаний (12.25), а второе, исходя из вида уравнения (13.2), будем искать в виде: х2(t) = A·cos(w·t + ),     (13.4) где A и  - постоянные величины, представляющие собой амплитуду и сдвиг фаз между смещением и внешней силой, которые требуется найти. Таким образом, общее решение x(t) будут иметь вид: x(t) = A0·e-·t·sin(·t + ) + A·cos(w·t + ).     (13.5) Из уравнения (13.5) следует, что в течение определенного промежутка времени осциллятор будет совершать сложное негармоническое движение, т. к. оно является результатом сложения двух колебаний, происходящих с разными частотами  и w). Однако через промежуток времени, равный нескольким значениям t = 1/, амплитуда, а следовательно, и энергия собственных колебаний существенно уменьшатся. При этом второе слагаемое останется неизменным, а значит результирующее колебание с течением времени станет гармоническим (см. рис. 13.1).
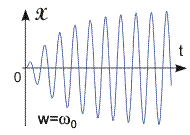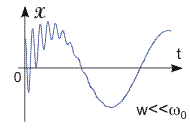Рис. 13.2. Графики вынужден-ных колебаний для случаев 0 = w и w << 0	Переходной и установившийся режимы колебаний. Гармонические колебания, которые будет совершать система через некоторое время после начала воздействия внешней силы, называются установившимися вынужденными колебаниями. Процесс релаксации колебаний называется переходным режимом (см. рис. 13.1, 13.2). Установившиеся колебания не зависят от начальных условий и описываются уравнением: х = A·cos(w·t + ).     (13.6) Частота вынужденных колебаний w равна частоте вынуждающей силы, а амплитуда A и сдвиг фаз смещения относительно внешней силы зависят от значений собственной частоты колебаний 0, частоты вынуждающей силы wи коэффициента затухания  (см. рис. 13.1, 13.2).
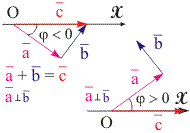Рис. 13.3. К расчету амплитудочастотной резонансной характеристики методом векторных диаграмм	Параметры вынужденных колебаний. Найдем величины А и установившихся вынужденных колебаний. Для этого подставим частное решение (13.6) и его производные по времени в выражение (13.2): - A·w·cos(w·t + ) - 2··w·A·sin(w·t + ) + A·2·cos(w·t + )  = F0·cos(w·t)/m.     (13.7) После преобразования (13.7) получим соотношение: A·(2 - w)·cos(w·t + ) - 2··w·A·sin(w·t + ) = F0·cos(w·t)/m.     (13.8) Найдем, при каких значениях А и будет выполняться соотношение (13.8), что и является по сути поиском частного решения неоднородного уравнения (13.2). Для этого воспользуемся методом векторных диаграмм. Каждое слагаемое в уравнении (13.8) последовательно представим в виде проекций на ось ОX векторов a, b и с, вращающихся относительно точки O с одной и той же постоянной угловой скоростью w (см. рис. 13.3). Взаимное расположение этих векторов относительно друг друга задается сдвигом фаз между соответствующими слагаемыми уравнения (13.8).  Обратите внимание, что если величина  > 0, то векторная диаграмма не замыкается, т.е. векторное равенство a + b = c      (13.9) не выполняется. Векторное равенство (13.9) может соблюдаться только в случае  < 0. Воспользовавшись теоремой Пифагора a2 + b2 = c2 для векторов, изображенных на рис. 13.3, получим: A2·((02 - w)2 + 4·2·w2) = (F0/m)2.     (13.10) Таким образом, значение амплитуды вынужденных колебаний равно: A = (F0/m)/((02 - w)2 + 4·2·w2)1/2.    (13.11) Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы и существенно зависит от соотношения между частотой вынуждающей силы и собственной частотой осциллятора. Зависимость A(w) называется амплитудочастотной характеристикой. Величину сдвига фаз между смещением и вынуждающей силой найдем как тангенс угла , равный отношению модулей векторов b и a (см. рис. 13.3). tg = - 2··w/(2 - w).     (13.12) Заметим, что смещение всегда отстает по фазе от вынуждающей силы (-  <  < 0) и зависит от соотношения частот w и ω0.
§ 2. Резонанс. Амплитудо- и фазочастотные характеристики Резонанс амплитуды. Анализ амплитудочастотной характеристики. Резонанс скорости. Фазочастотная характеристика осциллятора. Энергия установившихся вынужденных колебаний.
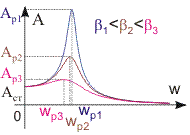Рис. 13.4. Амплитудочастотные характеристики осциллятора               резонансная частота                               физический смысл добротности	Резонанс амплитуды. Анализ амплитудочастотной характеристики. На рис. 13.4. изображены амплитудочастотные характеристики А(w) осцилляторов, совершающих колебания в средах с различными коэффициентами затухания β. Из рис. 13.4 видно, что функция А(w) зависит от величины коэффициента . Причем при определенном значении частоты вынуждающей силы амплитуда осциллятора становится максимальной. Явление, при котором амплитуда установившихся колебаний осциллятора достигает максимального значения, характерного для определенного значения частоты вынуждающей силы, называется резонансом. Частота вынуждающей силы, при которой амплитуда установившихся колебаний достигает своего максимального значения, называется резонансной. Приравнивая к нулю производную выражения (13.11) по частоте, получим формулы для расчета резонансной частоты wр и амплитуды Ар: wр = (2 - 2·2)1/2;     (13.13) Ар = F0/(2·m··0).     (13.14) В отсутствие трения, т.е. при  = 0 резонансная амплитуда стремится к бесконечности. Амплитуда, соответствующая значению частоты w = 0, называется статическим смещением Aст.  Под действием постоянной силы F0 частица отклоняется от положения равновесия на расстояние, равное Aст. Следовательно,  F0 = k·Aст и Аст = F0/k = F0/(m·02).     (13.15) Из выражения (13.11) следует, что при стремлении частоты вынуждающей силы к бесконечности амплитуда колебаний стремится к нулю. В этом случае система не успевает реагировать на достаточно быстрое изменение внешней силы и, несмотря на внешнее воздействие, будет находиться в положении равновесия. Из рис. 13.4 видно, что, чем меньше коэффициент затухания, тем ярче выражен резонанс. Рассмотрим отношение резонансной амплитуды к величине статического смещения. Из формул (13.14) и (13.15) следует, что это отношение постоянно для различных значений коэффициентов затухания и равно добротности системы: Ар/Аст = 0/2 = / = Q,     (13.16) где  - логарифмический декремент затухания. Добротность является важнейшей характеристикой резонансных свойств системы. Добротность задает отношение амплитуды колебаний осциллятора в резонансе к величине его статического смещения. Добротность также задает остроту пика амплитудочастотной кривой, которую принято измерять шириной Δw на половине высоты этого пика. Можно показать, что при малом затухании соблюдается равенство Δw =  или ω0/Δw = Q. Чем выше добротность, тем острее амплитудочастотная кривая. Явление резонанса имеет как положительные, так и отрицательные стороны. При резонансе могут разрушаться различные механические конструкции, например, мосты, валы турбин, здания. К положительным моментам использования явления резонанса относится, например, прием слабых электромагнитных сигналов с помощью резонансных контуров электрических цепей, разрушение бактерий ультразвуковой механической волной.
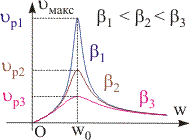Рис. 13.5. Зависимость амплитуды скорости установившихся вынужденных колебаний от их частоты   сравните рис. 13.4 и 13.5	Резонанс скорости. Амплитуда колебаний скорости υмакс для установившихся вынужденных колебаний, как следует из уравнения (13.4), равна: υмакс = Aυ = A·w. Воспользовавшись выражением (13.11) для амплитудочастотной характеристики, получим: υмакс = (F0·w/m)/((02 - w2)2 + 4·2·w2)1/2.     (13.17) Зависимость амплитуды скорости осцилляторов от частоты внешней гармонической силы приведена на рис. 13.5. Ее вид зависит от коэффициента затухания и несколько отличается от аналогичной зависимости для амплитуды смещения, а именно, значения скорости при w = 0 равняются нулю; резонансная частота амплитуды скорости не зависит от коэффициента затухания и равна собственной частоте колебаний при любых значениях коэффициента затухания. Это можно показать, продифференцировав выражение (13.17) по частоте и приравняв полученную производную к нулю.