1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 2. Сложение сонаправленных гармонических колебаний Сложение сонаправленных колебаний с кратными частотами.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 2. Сложение сонаправленных гармонических колебаний

Сложение сонаправленных гармонических колебаний с равными частотами.
Биения.
Сложение сонаправленных колебаний с кратными частотами.

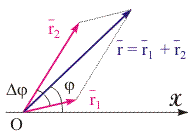
Рис. 11.8. Сложение сонаправленных колебаний с равными частотами методом векторных диаграмм.

Сложение гармонических колебаний одного направления с равными частотами. Пусть мы имеем два гармонических  колебания, описываемых законами:

x₁ = A₁·cos(·t +₁);
x₂ = A₂·cos(·t +₂).

(11.17)

Найдем их сумму х = x₁ + x₂. Данная задача эквивалентна нахождению результирующего колебания частицы, участвующей в двух гармонических процессах x₁(t) и x₂(t). Решим задачу простым, чем тригонометрическое сложение, способом. Для этого воспользуемся методом векторных диаграмм. В соответствии с этим методом зададим скалярные величины x₁ и x₂ в виде проекций векторов r₁ и r₂, вращающихся вокруг точки O с угловой скоростью . На рис. 11.8 представлено положение этих векторов и их проекций в момент времени  t = 0. 

Поскольку сумма проекций векторов r₁ и r₂, имеющих амплитуды A₁ и A₂, на ось OX равна проекции на эту же ось результирующего вектора r = r₁ + r₂, т.е.

r_1x + r_2x = (r₁ + r₂)_x,     (11.18)

то для получения искомого результата сначала по правилу сложения векторов (см. рис. 11.8) найдем r, а затем вычислим его проекцию. 

Так как в рассматриваемом примере колебания синхронные, то взаимная ориентация векторов r₁ и r₂ с течением времени не изменяется, и вектор r будет вращаться вокруг точки O со скоростью . Следовательно, результирующее колебание будет гармоническим, при этом в произвольный момент времени проекция r_x задается уравнением (11.19):

r_x  = x =  A·cos (·t + .     (11.19)

В уравнении (11.19) значения амплитуды A и угла  определяются в соответствие с выражениями (11.20) и (11.21):

A² = A₁² + A₂² + 2A₁·A₂·cos();     (11.20)
tg = (A₁·sin ₁ + A₂·sin ₂)/(A₁·cos ₁ + A₂·cos ₂).     (11.21)

Такой же результат получается исходя из представления колебаний в комплексной форме. В данном случае сначала производится сложение гармонических колебаний, представленных в виде векторов на комплексной плоскости, а затем находится действительная часть результирующего вектора как его проекция на действительную ось. Графическое отображение этих операций похоже на случай, изображенный на рис. 11.8. Похожий пример рассмотрен в задачах.

Величины A и  задают проекцию вектора r в начальный момент времени  x₀ =  A·cos . Из уравнений (11.20) и (11.21) следует, что амплитуда результирующего колебания зависит не только от соотношения амплитуд исходных колебаний, но и от сдвига фаз между ними  = ₂ - ₁.

Пример. Если ₂ = ₁, то амплитуда результирующего колебания равна сумме амплитуд A = A₁ + A₂, 
если ₂ - ₁ = , то их разности  A = A₁ - A₂ (при A₁ = A₂ амплитуда результирующего колебания равна нулю).




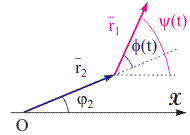
Рис. 11.9. Сложение сонаправленных колебаний с разными частотами методом векторных диаграмм.

Биения. Рассмотрим сложение гармонических колебаний одного направления с разными частотами. Пусть выполняется неравенство ₁ > ₂. Сначала проанализируем случай, когда разность частот складываемых колебаний мала (случай близких частот, т. е. ₁ - ₂ =  << ₁, ₂):

x₁ =  A₁·cos (₁·t + ₁    (11.22)
x₂ =  A₂·cos (₂·t + ₂    (11.23)

Найдем результирующее колебание x = x₁ + x₂. Заменив величину ₁ на ₂ + , запишем уравнение 1-го колебания в виде:

x₁ =  A₁·cos (₂·t + (·t + ₁A₁·cos (₂·t + (t   (11.24)

Величину(t будем рассматривать как медленно изменяющуюся со временем фазу (t = ·t + ₁. При этом угол (t)(t - φ₂ между векторами r₂ и r₁ изменяется по закону  (t)= ·t + и оба они вращаются с постоянной угловой скоростью ω₂ относительно точки O. С учетом вышеизложенного изобразим r₁ и r₂ на векторной диаграмме, как показано на рис. 11.9.

В результате проведения операции сложения  получим вектор r = r₁ + r₂, который вращается с постоянной угловой скоростью ₂, причем длина этого вектора периодически меняется со временем от значения, равного сумме A₁ + A₂, до значения, равного разности A₁ - A₂. Из уравнения (11.20) следует, что для произвольного момента времени:

A² = A₁² + A₂² + 2A₁·A₂·cos(·t + ),    (11.25)
где  = ₁ - _2,

т.е. амплитуда результирующего колебания А изменяется по гармоническому закону с частотой и периодом Т_б, равным:

Т_б = 2/.    (11.26)

Обратите внимание, что одновременно с этим процессом проекция результирующего вектора r на ось OX также изменяется согласно гармоническому закону, но с другими значениями частоты и периода, равными₂ и Т = 2π/₂ соответственно.
 


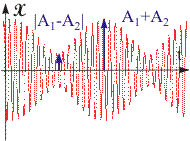
Рис. 11.10. График биений.

Амплитудно-модулированное колебание с медленно меняющейся амплитудой, являющееся результатом сложения сонаправленных гармонических колебаний с близкими частотами, называется биением.

График биений имеет вид, представленный на рис. 11.10. Видно, что результирующее колебание не является гармоническим (несущая частота равняется ₂, а частота изменения амплитуды равна ).

Наблюдать биения вы сможете с помощью следующей демонстрации. 

Пример. Если два камертона заставить звучать с близкими частотами, то в результате сложения колебаний громкость звука, обусловленная амплитудой суммарного колебания, периодически меняется с частотой биений. Высота же звука существенно не меняется, т.к. она определяется частотой результирующего колебания, которая близка к частотам складываемых колебаний.

Метод биений является чувствительным методом определения разницы частот.

 

 

Сложение сонаправленных колебаний с кратными частотами. Если складываемые колебания имеют резко отличающиеся частоты, то результирующее колебание в общем случае не будет периодическим. Если частоты складываемых колебаний кратны, т.е. ₁/₂ = n₁/n₂ (n₁ и n₂ - целые числа), то результирующее колебание, не являясь гармоническим, окажется периодическим. Период результирующего колебания будет равен наименьшему общему кратному (НОК) периодов складываемых гармонических колебаний.

Докажем это утверждение. Исходя из определения циклической частоты, T₂·n₂ = T₁·n₁ = С, где С - константа, являющаяся общим кратных периодов T₁ и T₂ (поскольку результат деления С на любой из этих периодов равен целому числу). С другой стороны, воспользовавшись методом векторных диаграмм, можно показать, что через целое число периодов складываемых колебаний n₁ и n₂ вектора r₁, r₂ и результирующий вектор r займут исходное положение, т.е. С - величина, кратная периоду T результирующих колебаний. Поскольку период колебаний равен наименьшему промежутку времени по истечение которого движение полностью повторяется, то его значение можно рассчитать как T = C/n, где n - общий делитель целых чисел n₁ и n₂. Таким образом, период результирующего колебания T есть НОК периодов T₁ и T₂ складываемых гармонических колебаний.

Например, если Т₁ = 2 с, Т₂ = 3 с, то Т = 6 с.