1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 1. Собственные незатухающие колебания Понятие собственных колебаний. Пружинный маятник. Математический и физический маятники. Крутильные колебания. Уравнение динамики гармонического осциллятора. Линейные и нелинейные системы. Ангармонические колебания.
Пример собственных колебаний.           Рис. 12.1. Иллюстрация квазиупругой силы.	Cобственные колебания. Колебания с точки зрения вызывающих их причин делятся на собственные и вынужденные. Собственными (свободными) называются колебания, которые совершает система исключительно под действием внутренних сил. Отметим, что собственные колебания сами по себе не возникают. Для их возбуждения систему необходимо предварительно вывести из положения равновесия. В дальнейшем за счет внутренних сил колебания будут продолжаться самостоятельно. Рассмотрим примеры собственных колебаний и условия их возникновения. Пружинный маятник. Пусть система состоит из тела, скрепленного с пружиной (см. рис. 12.1). Будем считать, что все упругие свойства сосредоточены в пружине, а ее масса пренебрежимо мала по сравнению с массой тела. Примем точку O, соответствующую положению тела при недеформированной пружине, за начало отсчета х0 = 0 (см. рис. 12.1). Предположим, что сила трения в системе отсутствует Fтр = 0. В случае смещения тела из положения равновесия в системе возникает сила упругости, действующая на тело и стремящаяся возвратить его в равновесное состояние. Поскольку при малых деформациях проекция силы упругости на ось X рассчитывается в соответствии с законом Гука F = -k·x, то второй закон Ньютона в проекции на направление движения будет иметь вид: m·aх = -k·x или     x" + ω02·х = 0, (12.1) где ω0 = (k/m)1/2 - постоянная для данной системы величина. Выражение (12.1) представляет собой уравнение, в  которое входит искомая функция x(t), ее вторая производная x'' (мгновенное ускорение) и параметр ω0. Уравнения такого типа называются дифференциальными уравнениями второго порядка. Поскольку переменная t в уравнение (12.1) в явном виде не входит, то оно является однородным. Более того, искомая функция и ее производные входят в уравнение (12.1) в первой степени и оно является линейным. Итак, выражение (12.1) представляет собой линейное однородное дифференциальное уравнение второго порядка. Общим решением дифференциальных уравнений является такая функция x(t), которая при подстановке обращает их в тождество при любых значениях входящих в него параметров. В теории дифференциальных уравнений показано, что общее решение (12.1) выражается зависимостью вида: x = A·cos(ω0·t + φ0),   (12.2) где ω0 - собственная частота колебаний. Если груз подвешен на вертикально расположенной пружине, то уравнение динамики в проекции на вертикальную ось примет вид: m·x'' = -k·x + m·g, где x - величина отклонения груза от положения равновесия. Введем новую ИСО, тело отсчета которой свяжем с положением покоящегося под действием сил тяжести и упругости груза xg. Отклонение груза от положения равновесия в этой СО x будет равно: x = x - xg. В результате несложных преобразований, учитывая, что x'' = x'', получим уравнение динамики пружинного маятника в новой СО: m·x'' = -k·x - k·xg + m·g = -k·x. Таким образом, наличие дополнительной постоянной силы (силы тяжести) не изменяет вида закона движения груза (12.2), если выбрать новое положение тела отсчета. Итак, необходимыми условиями возникновения собственных гармонических колебаний пружинного маятника являются наличие упругой силы, подчиняющейся уравнению (12.3), и отсутствие диссипативных сил. F = -k·x,    (12.3) где F - равнодействующая сил, приложенных к телу. Обратите внимание на то, что собственная частота колебаний пружинного маятника ω0 задается физическими свойствами системы и не зависит от начальных условий. Таким образом, ω0 - характеристика пружинного маятника.
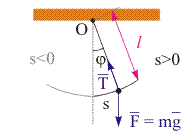Рис. 12.2. Математический маятник.	Математический маятник. Математическим маятником называется система, состоящая из тела, которое подвешено на длинной невесомой нерастяжимой нити и совершает колебательное движение в вертикальной плоскости вокруг точки подвеса. Поскольку длина нити много больше размеров тела, то его можно считать материальной точкой. Маятник, будучи выведенным из положения равновесия, начнет совершать вращательное движение в вертикальной плоскости относительно точки подвеса. Введем обозначения: O - точка подвеса маятника; С - положение колеблющегося тела; l - длина маятника (длина нити); φ - угол отклонения от положения равновесия. Закон движения математического маятника в проекции на направление элементарного перемещения ds имеет вид: m·s'' = -m·g·sin φ,   (12.4) где s'' - вторая производная от дуговой координаты s по времени, отсчитываемой от положения равновесия. В случае малых колебаний, когда с достаточной степенью точности выполняется равенство sin φ = φ, уравнение динамики математического маятника можно записать как s'' + g·φ = 0. Поскольку φ = s/l, то s'' = φ''·l, и уравнение движения математического маятника примет вид: φ'' + (g/l)·φ = 0.   (12.5) Выражение (12.4) по сути совпадает с (12.2), в которое в качестве изменяющейся величины входит угловое смещение от положения равновесия φ, а в качестве параметра ω02 выступает величина g/l. Решение уравнения (12.5) имеет следующий вид: φ(t) = φmax·sin(ω0·t + φ0),   (12.6) где ω0 = (g/l)1/2.   (12.7) Таким образом, математический маятник совершает гармоническое вращательно-колебательное движение относительно точки O и является линейным осциллятором.
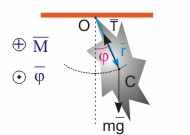Рис. 12.3. Физический маятник.	Физический маятник. Физическим маятником называется твердое тело, совершающее вращательные колебания относительно закрепленной точки, жестко связанной с этим телом. Введем обозначения: O - точка подвеса; С - положение центра масс маятника; r - длина физического маятника, равная расстоянию от точки подвеса до его центра масс; φ - угол отклонения от положения равновесия. На маятник действуют сила тяжести m·g и упругой деформации T. Основное уравнение динамики вращательного движения для физического маятника в проекции на ось вращения, проходящую через точку O, имеет вид: Mz = I·φ''.   (12.8) Исходя из рис. 12.3, поворот маятника вокруг точки подвеса может произойти только под действием на тело момента силы тяжести, причем ось вращения будет перпендикулярна плоскости рис. 12.3. Проекция момента силы тяжести на эту ось равна: Mz = -m·g·r·sin φ. Для малых углов справедливо выражение: Mz = -m·g·r·φ.  (12.9) Закон движения физического маятника можно преобразовать к виду: φ'' + (m·r·g/I)·φ. = 0.  (12.10) Выражение (12.10) в точности совпадает с (12.5), где в качестве параметра ω02 выступает величина m·r·g/I. Решение уравнения (12.10) имеет следующий вид: φ(t) = φmax·sin(ω0·t + φ0),   (12.11) где ω0 = (m·g·r/I)1/2.   (12.12) Таким образом, физический маятник совершает гармоническое вращательно-колебательное движение относительно закрепленной точки O и является линейным осциллятором. Собственную частоту колебаний физического маятника можно представить в виде, аналогичном выражению (12.7) для математического маятника: ω0 = (g/lприв)1/2,   (12.13) где lприв = I/(m·l) - приведенная длина физического маятника.
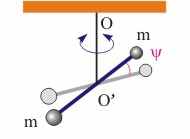Рис. 12.4. Крутильные колебания.	Крутильные колебания (см. рис. 12.4). Рассмотрим систему, изображенную на рис. 12.4. Введем обозначения:  - угловая координата,  I - момент инерции системы грузов и подвеса. Уравнение динамики для этой системы в проекции на ось вращения имеет вид: I· = -K·       или '' = -(K/·.     (12.14) где К - постоянная системы Сравнивая уравнения (12.5) и (12.14), видим, что они аналогичны. Следовательно, решение уравнения (12.14) имеет вид гармонической функции: (t) = max·sin((K/I)1/2·t + 0),     (12.15) а система представляет собой гармонический осциллятор.
	Уравнение динамики гармонического осциллятора. Обобщим результаты, полученные для различных колеблющихся систем. Мы показали, что если закон движения системы имеет вид (12.1), то она является гармоническим осциллятором. Уравнение (12.1) есть уравнение динамики гармонического осциллятора, а его решение (12.2) является уравнением гармонических колебаний. Свободные колебания любого осциллятора в отсутствие диссипативных сил будут гармоническими в случае, если результирующая сила, действующая на него, направлена к положению равновесия и зависит от величины смещения из этого положения по линейному закону (для случая вращательного движения вектор результирующего момента сил направлен против вектора углового смещения). Сила, направленная к положению равновесия и зависящая от величины смещения от этого положения по линейному закону, называется квазиупругой. Наличие квазиупругой силы является критерием малых колебаний. Линейные и нелинейные системы.  Очевидно, что далеко не всегда колебания системы являются малыми, а сила - квазиупругой. Поставим вопрос несколько иначе. Существуют ли определенные условия для произвольных систем, при которых действующую в них возвращающую силу можно считать квазиупругой? Для ответа на этот вопрос воспользуемся понятием потенциальной энергии. Любую функцию в окрестности некоторой точки x0 можно представить в виде бесконечного ряда - ряда Тейлора: f(x) = f(x0) + f'(x0)·(x - x0) + f''(x0)·(x - x0)2/2! + + f'''(x0)·(x - x0)3/3! + ...    (12.16) Воспользуемся формулой (12.16) и разложим потенциальную энергию в ряд Тейлора вблизи положения равновесия системы - точки c координатой x0 = 0. Ввиду незначительности отклонения от положения равновесия системы в случае малых колебаний x - x0 << 1 ограничимся первыми тремя слагаемыми ряда (чем больше порядок слагаемого, тем меньше его вклад в сумму). Eп(x) = Eп(0) + Eп'(0)·x + Eп''(0)·x2/2. Известно, что в положении устойчивого равновесия первая производная от потенциальной энергии по координате равняется нулю, а вторая - имеет положительное значение. Следовательно, Eп(x) = Eп(0) + k·x2/2,   (12.17) где k - положительная постоянная. Найдем выражение для консервативной силы, которая соответствует виду потенциальной энергии, задаваемой соотношением (12.17). Поскольку Fx = -dEп/dx, то Fx = -k·x, что соответствует критерию квазиупругой силы. Уравнение динамики такой системы имеет вид (12.1), а сама система называется линейной. Следовательно, система, находящаяся в состоянии, близком к равновесному, в отсутствии диссипативных сил является линейной и, следовательно, совершает гармонические колебания. Чем больше отклонение от положения равновесия, тем в меньшей степени можно ограничиться приближением (12.17). Такие системы называются нелинейными, и их колебания не являются гармоническими. Ангармонические колебания. Рассмотрим в качестве одного из примеров нелинейной системы большие колебания физического маятника. Его движение описывается следующим нелинейным уравнением: φ'' + ω02·sin φ = 0.   (12.18) Решение уравнения (12.18) уже не является гармоническими колебаниями. Такие колебания будут ангармоническими. Период ангармонических колебаний зависит от их амплитуды φmax. Приближенная формула для его расчета имеет вид: T = T0·(1 + φmax2/16),   (12.19) где T0 - период соответствующих малых гармонических колебаний.
§ 2. Собственные затухающие колебания Уравнение динамики затухающих колебаний. Коэффициент затухания и его физический смысл. Логарифмический декремент затухания. Добротность.
Движение тела в вязкой среде. 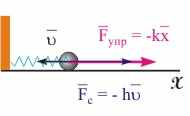Рис. 12.5. Иллюстрация силы вязкого трения.	Уравнение динамики затухающих колебаний. В реальных ситуациях на тело, совершающее собственные гармонические колебания, действуют диссипативные силы. Наиболее распространен случай вязкого трения, когда диссипативные силы пропорциональны скорости движения тела в вязкой среде: Fтр = -h·,      (12.20) где h - коэффициент сопротивления среды.  Уравнение (12.20) справедливо, например, при медленном движении тел в жидкости. По мере увеличения скорости в правой части уравнения (12.20) появляются слагаемые более высокого порядка (пропорциональные квадрату, кубу скорости и т. д.). В вязкой среде, когда справедливо уравнение (12.20), закон движения тела в проекции на ось X (см. рис. 12.5) будет иметь вид: m·x'' = -k·x -h·x'.    (12.21) После несложных преобразований получим: x'' + (h/m)·x' + (k/m)·x = 0;       x'' + 2··x' + 2·x = 0,    (12.22) где  h/(2m) - коэффициент затухания.
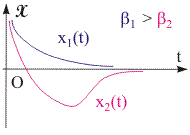Рис. 12.7. График затухающих колебаний в случае большого трения.	Решение уравнения динамики для случая сильного и слабого трения. Общее решение линейного дифференциального уравнения (12.22) будем искать в комплексном виде: x(t) = A0·ei··t+,     (12.23) где i = (-1)1/2 - мнимая единица;   - константа , значение которой определяет частоту колебаний системы при наличии вязкого трения. Подставив (12.23) в уравнение затухающих колебаний, получим выражение для расчета α: -α2 + 2··α·i + 2·x = 0. Решение этого квадратного уравнения будет выглядеть следующим образом: 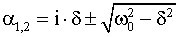.   (12.24) Исходя из (12.24), решение дифференциального уравнения (12.23) будет разным в зависимости от величины коэффициента сопротивления. Слабое трение. В случае малого сопротивления среды  <  из уравнений (12.23) и (12.24) следует, что: x(t) = A0·e-·t·e+/-i·ω·t+.     Действительная часть полученного комплексного выражения в случае знака плюс перед квадратным корнем в уравнении (12.24) есть уравнение собственных затухающих колебаний: x(t) = A0·e-·t·sin(·t + ).   (12.25) где ω - циклическая частота затухающих колебаний, равная ω  = (2 - 2)1/2   (12.26) Величины A0 и  определяются начальными условиями, а циклическая частота затухающих колебаний  - характеристиками колеблющейся системы и окружающей среды. Наличие трения уменьшает частоту колебаний. Качественно этот факт можно объяснить следующим образом. Сила вязкого трения действует против скорости. Следовательно, в модели  линейной системы ее действие эквивалентно уменьшению квазиупругой силы. Это означает, что частота затухающих колебаний , зависящая от коэффициента k, также уменьшается, а их период Т - увеличивается. 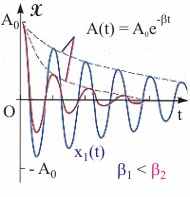Рис. 12.6. График затухающих колебаний в случае малого трения. При слабом трении  << ω0 частота затухающих колебаний приблизительно равна собственной, а выражение A0·e-·t, стоящее перед функцией синус в уравнении (12.26), можно рассматривать как медленно меняющуюся амплитуду колебаний. График затухающего колебания представляет собой амплитудно-модулированную синусоиду (см. рис. 12.6). Модулирующая функция является экспоненциальной и описывается уравнением (12.27):  А(t)  = A0·e-·t.     (12.27) Колебания при наличии затухания не являются гармоническими и даже периодическими. Условно, за период слабо затухающих колебаний можно принять минимальный промежуток времени между локальными максимумами или минимумами функции x(t) (см. рис. 12.8). Сильное трение. При сильном трении  > ω0 решение уравнения динамики является действительным и имеет вид (12.28). Физический смысл имеет решение со знаком минус перед квадратным корнем в уравнении (12.24), иначе при >> ω0 колебания x(t) вообще не будут затухать: x(t) = A0·e-( + ( - )1/2)·t+.     (12.28) В данном случае система колебаний как таковых не совершает (кривая x1(t) на рис. 12.7). Будучи выведенной из положения равновесия, она апериодически (без осцилляций) возвращается в равновесное состояние. Возможен также и промежуточный вариант между случаями сильного и слабого трения (кривая x2(t) на рис. 12.7).
	Коэффициент затухания. Коэффициент , определяющий быстроту изменения амплитуды, называется коэффициентом затухания. Если промежуток времени между измерением амплитуд соседних циклов колебаний равен  t = 1/, то как следует из (12.27), их отношение равно основанию натурального логарифма А0/А = е. Отсюда вытекает физический смысл коэффициента затухания:  величина 1/, равна промежутку времени, по истечении которого амплитуда колебаний уменьшается в е раз (e  основание натурального логарифма, е = 2.7318).
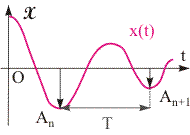Рис. 12.8. К определению логарифмического декремента затухания.	Логарифмический декремент затухания, добротность. Коэффициент затухания  не дает полного представления об интенсивности затухания. Пусть два осциллятора совершают затухающие колебания с разными частотами, причем амплитуда колебаний достигла определенного малого уровня через одинаковые промежутки времени. Но для первого из них это произошло по истечении промежутка времени, равного 10 периодам соответствующих колебаний, а для второго - 100. Остается неясным, какой осциллятор обладает более быстрым затуханием. Для характеристики интенсивности затухания вводят понятие логарифмического декремента затухания. Пусть Т - условный период затухающего колебания, Аn и An+1 - амплитудные значения функции x(t) для двух ее последовательных экстремумов (см. рис. 12.8). Величина , равная  = ln(Аn /An+1), называется логарифмическим декрементом затухания.   = ln(Аn /An+1).   (12.29) Установим связь между величинами  и : = ln( Аn /An+1) = ln(A0·e -·t/A0·e -·(T + t)) = ln(e·T) =  =  ·T.    (12.30) Используя уравнение (12.30), можно преобразовать закон затухания амплитуды колебаний: An = A0·e-·t = A0·e-·T·t/T = A0·e-·n,     (12.31) где n = t/T - число колебаний, совершенных за время t. Из уравнения (12.31) следует, что если n = 1/, то A0/An = e = 2.7318.  Величина 1/ равна числу колебаний, по истечение которых их амплитуда уменьшается в е раз. Если значение  мало ( << 1), то можно показать, что логарифмический декремент затухания равен относительному изменению амплитуды колебаний за условный период T: (An - An+1)/An = .     (12.32) Для характеристики колебаний также используют величину, называемую добротностью. Добротность системы Q  величина, равная отношению числа π к логарифмическому декременту затухания. Q = /.     (12.33) Добротность равна произведению числа колебаний, по истечении которых их амплитуда уменьшится в e раз, на число . На физическом смысле добротности более подробно остановимся в теме 13.
§ 3. Энергия собственных колебаний Полная механическая энергия собственных незатухающих колебаний. Полная механическая энергия собственных затухающих колебаний.
	Полная механическая энергия незатухающих колебаний. Рассмотрим груз на пружине, совершающий собственные незатухающие колебания. Так как Fтр = 0, то система "грузпружина" является замкнутой, консервативной и согласно закону сохранения ее полная механическая энергия, равная сумме кинетической и потенциальной составляющих, не изменяется: E = Ек + Еп = const.     (12.34) Рассчитаем полную механическую энергию Е гармонического осциллятора, совершающего колебания по закону x = A·sin(·t +0). При выводе выражения для расчета Еп учтем, что k = 2· m. Выражения для Ек и Еп будут иметь следующий вид: Ек = m·2/2 = m·A2·2/2·cos2(·t +0); Еп = k·x2/2 = m·A2·2/2·sin2(·t +0). (12.35) Просуммировав уравнения системы (12.35) и учтя определение (12.34), получим, что полная механическая энергия гармонического осциллятора пропорциональна квадратам амплитуды и собственной частоты: E = m·A2·2.     (12.36) Полная механическая энергия собственных незатухающих колебаний постоянна, но при этом кинетическая и потенциальная энергии изменяются с течением времени по гармоническому закону с частотой равной 2. Из закона сохранения полной механической энергии следует, что по мере совершения колебаний кинетическая энергия системы переходит в потенциальную и наоборот (см. рис. 12.9), а максимальные значения кинетической и потенциальной энергий равняются значению полной механической энергии. 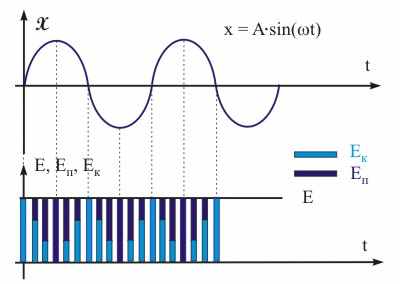                   Рис. 12.9. Превращение энергии в случае колебательного движения груза на пружине. Выражение для полной механической энергии как суммы ее кинетической и потенциальной составляющих есть уравнение фазовой траектории осциллятора, представляющее собой эллипс. Действительно, E = m·υ2/2 + k·x2/2 = const или υ2/(2E/m) + x2/(2E/k) = 1.  Периодическое движение осциллятора по фазовой траектории соответствует взаимообразному переходу кинетической энергии в потенциальную при сохранении полной механической энергии системы.
Рис. .12.10. Зависимость полной механической энергии затухающих колебаний от времени.	Полная механическая энергия собственных затухающих колебаний. В случае слабого трения  <<  полная механическая энергия системы с течением времени уменьшается, но ее изменением за условный период колебаний согласно (12.32) можно пренебречь. Подставив выражения для кинетической и потенциальной энергии затухающих колебаний в формулу (12.34), получим: E = Ек + Еп = m·2/2 + k·x2/2 = = (m·A2(t)·2·cos2(·t + 0) + k·A2(t)·sin2(·t + 0))/2 = = m·A2(t)·(2·cos2(·t + 0) + 2·sin2(·t + 0))/2. (12.37) Следовательно, полная механическая энергия затухающих колебаний не постоянна. Она уменьшается с течением времени согласно соответствующему закону изменения амплитуды A2(t) = A02·e-2··t, совершая при этом колебания с частотой, равной 2ω (см. рис. 12.10). Эти осцилляции тем меньше, чем ближе частота затухающих колебаний системы к собственной частоте. В данном случае полная механическая энергия осциллятора изменяется по экспоненциальному закону (12.38). E(t) = m·A02·2·e-2··t/2 = Е0·e-2··t.     (12.38)
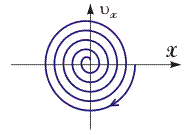Рис. .12.11. Фазовая траектория затухающих колебаний.	Фазовая траектория затухающих колебаний при действии сил трения, пропорциональной скорости, представляет собой закручивающуюся относительно начала координат спираль (см. рис. 12.11). По мере затухания колебаний энергия системы уменьшается и значение радиус-вектора осциллятора в фазовой плоскости уменьшается. Число витков спирали равно числу колебаний, которое успеет совершить осциллятор за время его движения.