Geum.ru

1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материалаДокументы

Содержание


§1. Общая характеристика гармонических колебаний и формы их представления
Колебательные процессы в механике.
В механических колебаниях речь идет об изменениях величин линейного или углового смещения тела.
Гармоническими называются колебания в любой физической системе, которые описываются величиной, изменяющейся по закону синуса или
Величина А, равная наибольшему отклонению колеблющейся физической величины от положения равновесия, называется амплитудой колеба
Частота - есть число колебаний осциллятора за одну секунду.
Кинематические характеристики гармонических колебаний.
Фазовые траектории гармонического осциллятора.
Подобный материал:
1   ...   16   17   18   19   20   21   22   23   ...   35



§1. Общая характеристика гармонических колебаний и формы их представления
Колебательные процессы в механике.
Понятие гармонических колебаний. Гармонический осциллятор.
Параметры колебаний и их физический смысл.
Кинематические характеристики гармонических колебаний.
Фазовые траектории гармонического осциллятора.
Представление гармонических колебаний с помощью метода векторных диаграмм.
Представление гармонических колебаний в комплексной форме.


Демонстрация колебаний пружинного маятника.
Колебательные процессы в механике. В природе существует большое количество разнообразных повторяющихся через определенные промежутки времени процессов различной природы, например, движение Солнца, работа сердца, протекание переменного электрического тока, распространение электромагнитного поля и т. д. Естественно попытаться провести описание такого рода физических процессов с единой точки зрения, учитывая указанное выше свойство  повторяемость.

Колебание – многократно повторяющийся или приблизительно повторяющийся процесс, характеризующийся изменением значения физической величины около ее равновесного значения.

В механических колебаниях речь идет об изменениях величин линейного или углового смещения тела.

Примеры механических колебаний: движение груза, связанного с деформированной пружиной; колебания тела, подвешенного на нити; движение поршня двигателя внутреннего сгорания.

Механические колебания являются одним из частных случаев движения, но описание физической сущности этого процесса не ограничивается только решением задачи по определению значения координаты физического объекта и его скорости в произвольный момент времени. Принципиально важным является анализ поведения колеблющейся системы за достаточно длительный временной интервал, существенно больший периода колебаний. Например, эффект воздействия звука на человеческое ухо определяется не только конкретным значением величины отклонения барабанной перепонки от равновесного положения, но и совокупностью серии многих циклов ее колебательного движения.

Уравнения колебаний служат основой для описания волновых процессов различного рода, таких как механические, электромагнитные и, следовательно, несмотря на их различную природу нуждаются в рассмотрении с единых позиций.

Форма колебаний может быть разной (см. рис. 11.1). Выделяют непериодические и периодические колебания.

Периодическими называются колебания, для которых значения физической величины повторяются на протяжении всего колебательного процесса через некоторый постоянный временной интервал T.
Минимальная величина этого интервала называется периодом колебаний.

Для периодических колебаний для любого момента времени t выполняется соотношение f(t) = f(t + n·T), где f(t) - анализируемая функция; n - целое число.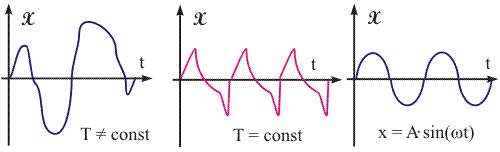


Рис. 11.1. Примеры колебаний некоторой величины x.

 
Понятие гармонических колебаний. Гармонический осциллятор. Среди всех периодических колебаний особая роль отводится гармоническим колебаниям.

Гармоническими называются колебания в любой физической системе, которые описываются величиной, изменяющейся по закону синуса или косинуса.

Физическая система, совершающая гармонические колебания, называется линейным (гармоническим) осциллятором.

Теория механических гармонических колебаний имеет важное значение ввиду следующих причин:
распространенность данного вида движения;



возможность обобщения на другие, немеханические физические процессы;



возможность анализа на основе теории гармонических колебаний любых периодических процессов, поскольку любое периодическое колебание можно представить в виде суммы гармонических составляющих.

Уравнение гармонических колебаний имеет следующий вид:

x = A·cos(ω·t +0),     (11.1)
где х - значение колеблющейся величины;
t - время;
А, ω,  - константы, характерные для данного колебания.

 

 
Параметры гармонических колебаний и их физический смысл. Постоянные величины А, ω, , входящие в уравнение (11.1), называются параметрами колебания. Рассмотрим их физический смысл.

Из (11.1) следует, что при соs(ω·t + 0) = ±1 значение модуля величины x максимально, т.е. |x| = xmax = A.

Величина А, равная наибольшему отклонению колеблющейся физической величины от положения равновесия, называется амплитудой колебания.

Установим связь между периодом колебаний и параметром ω. Поскольку период функции косинус равняется 2π, то, исходя из определения периода колебаний, через временной интервал, равный произведению n·T, аргумент функции косинус изменится на величину, кратную 2π. При этом величина х примет свое предыдущее значение. Таким образом для любого момента времени t выполняются следующие равенства:

x(t) = x(t + n·T),
ω∙n·T = 2π∙n,
где Т - период;
n - целое число.

Из последнего уравнения следует физический смысл параметра ω, называемого циклической частотой колебаний. Т.к.

 = 2/Т, то     (11.2)

циклическая частота  - есть число колебаний осциллятора за 2π секунд.

Единица измерения циклической частоты - радиан в секунду (рад/с).

Величина, обратная периоду колебаний Т, называется частотой ν = 1/Т = /2. Частота - есть число колебаний осциллятора за одну секунду. Единица измерения частоты - герц. 1 Гц = 1 с-1.

Мгновенное значение физической величины х определяется фазой колебаний Ф, равной:

Ф = ·t + 0.     (11.3)


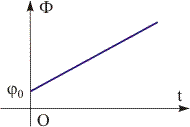Рис. 11.2. Зависимость фазы гармонических колебаний от времени.
Фаза гармонических колебаний Ф линейно растет со временем (см. рис. 11.2). При t = 0 значение Ф равняется 0, которое называется начальной фазой. Начальная фаза задает значение x в начальный момент времени.

Начальную фазу и амплитуду гармонического осциллятора можно рассчитать исходя из начальных условий, подставив в уравнение колебательного движения (11.1) и выражение для его скорости υ = dx/dt значение времени t = 0. Проделав соответствующие операции, получим:

х(0) = х0 = А·cos(0).
0 = -А··sin(0).
где υ - скорость колеблющейся системы.

Решив эту систему уравнений, получим, что величины амплитуды и начальной фазы определяются начальными условиями для рассматриваемой системы.

A = (x02 + υ02/ω2)1/2;    (11.4)
tg φ0 = -υ0/(x0·ω).    (11.5)

Примеры. Если груз на пружине отклонить от положения равновесия и отпустить с нулевой скоростью, то начальные условия примут вид: x(0) = х0, υ0 = 0. Подставив эти значения в (11.4) и (11.5), получим, что колебание груза описывается уравнением x = A·cos (ω·t).

Если колебания груза инициируется толчком из положения равновесия, то начальные условия примут вид: x(0) = 0, 0. Подставив эти выражения в (11.4) и (11.5), получим, что колебание описывается уравнением
x = 0/ω·sin(ω·t).

Большое значение для анализа сложного колебательного движения имеет понятие разности фаз (сдвига фаз) колебаний Ф.

Если колебания имеют одинаковую частоту, то величина Ф не зависит от времени, и они происходят с постоянным сдвигом фаз. Если колебания происходят с разными частотами, то величина Ф зависит от времени.


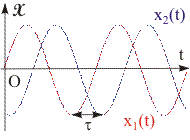Рис. 11.3. Вид колебаний с равными частотами.
Пример такого рода колебаний приведен на рис. 11.3. Колебание величины x1 = A1·sin(·t)  опережает колебание x2 = A2·sin(·(t - )), где  = const > 0.

Сдвиг фаз можно выразить в радианах и в долях периода. Пусть колебания подчиняются уравнениям:

x1 = A1·sin(2·t/T);
x2 = A2·sin(2·(t - )/T),
(11.6) 
где  - время запаздывания 2-го колебания
относительно 1-го.

Второе колебание можно представить в следующем виде:

x2 = A2·sin(2·t/T - 2·/T).     (11.7)

Очевидно, что

1 - 2 = 2·/Т.     (11.8)

Из уравнения (11.8) следует, что если  = Т/4, то 1 - 2 = /2, а при  = Т/2, сдвиг фаз 1 - 2 = .


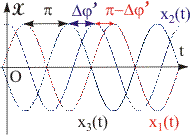Рис. 11.4. К понятию сдвига фаз колебаний.
Колебания, происходящие со сдвигом фаз , называются противофазными (кривые x1 и x3 на рис. 11.4). Имеется некоторая неопределенность в отставании и опережении на угол . Нельзя сказать, которое из колебание отстает по фазе от другого, а какое опережает, т. к. математически эти утверждения эквивалентны. Для устранения этой неопределенности условились сдвиг фаз задавать в диапазоне от 0 до . 

Рассмотрим случай, когда колебание х2 отстает по фазе от х1 больше, чем на  (см. рис.11.4). Сдвиг по фазе Ф1 - Ф2 =  + ' характеризует отставание 2-го колебания от 1-го. Из  рис.11.4 видно, что такое отставание эквивалентно опережению 2-м колебанием 1-го на угол Ф2 - Ф1 =  - '. Такой же результат получим в аналитическом виде, исходя из тригонометрического равенства:

sin( + ) = sin( - ).

Влияние параметров колебаний на их вид вы можете наблюдать на графиках, которые получите самостоятельно.
 

 
Кинематические характеристики гармонических колебаний. Найдем величины скорости и ускорения колебательного движения, описываемого уравнением:

x = A·sin(·t +0).     (11.9)

Поскольку скорость  - есть производная от координаты по времени, а ускорение - производная от скорости a = dυ/dt, то для гармонических колебаний, описываемых уравнением (11.8), эти величины зависят от времени также по гармоническим законам:

 = A··cos(·t +0) = A··sin(·t +0 + /2);     (11.10)
a = -A·2·sin(·t +0) = -2·x.   (11.11)

Для гармонических механических колебаний скорость опережает по фазе смещение на /2, а ускорение  на .

Наличие пропорциональной зависимости ускорения от величины смещения от положения равновесия (11.11) является характерным признаком гармонического колебательного движения.

Фазовые траектории гармонического осциллятора. Фазовая траектория гармонического осциллятора представляет собой собой эллипс (см. задачу 11-2). Во время колебаний изображающая их точка движется по эллипсу по часовой стрелке, совершая полный оборот за время T = 2π/ω. Максимальная скорость движения наблюдается в точке равновесия и, наоборот, при максимальном отклонении от положения равновесия значение скорости обращается в нуль.

Замкнутость фазовой траектории показывает, что движение носит периодический характер, а значение колеблющейся величины не выходит за пределы области от -A до +A.


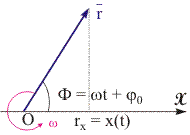Рис. 11.5. Иллюстрация метода векторных диаграмм
Представление гармонических колебаний с помощью метода векторных диаграмм. В ряде случаев оказывается полезным представить колебания скалярных величин с помощью векторов. Данный способ называется методом векторных диаграмм. Для представления величины x, изменяющейся по гармоническому закону в соответствии с уравнением (11.9), изобразим вектор r, исходящий из точки O (см. рис. 11.5). Пусть длина данного вектора равна амплитуде A колебаний, а угол между ним и координатной осью OX - фазе Ф. 

Допустим, что вектор r вращается вокруг точки O с угловой скоростью  против часовой стрелки, что соответствует положительному направлению отсчета углов. Тогда угол между вектором r и осью OX и фаза будут изменяться по закону Ф(t) = ·t +0. Значение физической величины x в любой момент времени зададим как проекцию вектора r на ось Х:

rx = x = A·cos(·t +0).     (11.12)

Итак, скалярное гармоническое колебание можно представить как проекцию вектора с амплитудой A, который вращается вокруг закрепленной точки O с постоянной угловой скоростью .


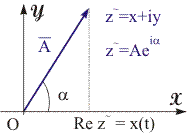Рис. 11.6. Представление комплексного числа в декартовой системе координат.
Представление гармонических колебаний в комплексной форме. Для представления гармонических колебаний в комплексной форме воспользуемся формулой Эйлера (11.13).

eiα = cos α +i·sin α,    (11.13)
где i = (-1)1/2 - мнимая единица.

Изобразим произвольное комплексное число z~ = x + i·y на плоскости XY. В декартовой системе координат действительную часть комплексного числа x обычно откладывают по оси абсцисс, а мнимую y - по оси ординат (см. рис. 11.6). Следовательно, любое комплексное число можно представить в виде вектора A на комплексной плоскости, проведенного из начала координат в точку с координатами {x, y}. Исходя из формулы Эйлера и представления z~ в виде суммы действительной и мнимой составляющих, любое комплексное число можно записать в экспоненциальной форме:

z~ = A·eiα, (11.14)
где A = (x2 + y2)1/2 - модуль комплексного числа;
tg α = y/x - фаза комплексного числа.

 


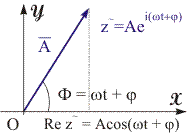Рис. 11.7. Представление гармонических колебаний на комплексной плоскости.
Перейдем к рассмотрению уравнения гармонических колебаний. Действительная или мнимая части выражения (11.14) есть функции косинуса и синуса (гармонические функции), следовательно, действительная Re z~ или мнимая Im z~ части функции z~ = A·ei(ω·t+φ), в соответствии с формулами (11.15), (11.16) есть уравнения гармонических колебаний:

Re z~ = A·cos (ω·t + φ);    (11.15)
Im z~ = A·sin (ω·t + φ).    (11.16)

Представление гармонических колебаний в комплексной форме пояснено на рис. 11.7. Гармоническое колебание - есть проекция на ось абсцисс комплексного числа z~, изображенного на комплексной плоскости в виде вектора A.