1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 1. Элементы гидростатики Свойства жидкостей. Закон сообщающихся сосудов. Закон Паскаля. Закон Архимеда. Условие плавания тел.
Сообщающиеся сосуды.	Свойства жидкости. Свойства жидкостей и газов благодаря своему молекулярному строению существенным образом отличаются от свойств твердых тел. Газ занимает весь объем сосуда, в котором находится, а сколь угодно малое силовое воздействие на жидкость способно изменить ее форму без изменения объема. Например, жидкость, находящаяся в поле силы тяжести, принимает форму сосуда, в котором она находится. Поверхность покоящейся жидкости перпендикулярна направлению действия силы тяжести независимо от формы сосуда. Гидростатика изучает равновесие жидкости и воздействие покоящейся жидкости на погруженные в не тела. Одним из законов гидростатики является закон сообщающихся сосудов: в сообщающихся сосудах однородная по плотности жидкость устанавливается на одном уровне.
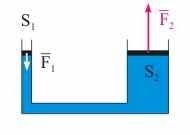Рис. 14.1. Гидравлический пресс.	Закон Паскаля. Давлением p в жидкости называется величина, равная отношению модуля силы F, действующей перпендикулярно выделенной площадке, к ее площади S: p = F/S.     (14.1) Закон Паскаля гласит: давление, оказываемое внешними силами, передается жидкостью одинаково по всем направлениям. На основе закона Паскаля работают различные гидравлические устройства, тормозные системы автомобилей, домкраты, прессы и т.п. В гидравлическом прессе малая сила F1, действующая на поршень малой площади S1, трансформируется в большую силу F2, действующую на большой поршень S2 (см. рис. 14.1). Действительно, согласно закону Паскаля p = F1/S1 = F2/S2. Следовательно, F2 = F1·S2/S1 > F1. Давление на жидкость оказывают окружающие ее физические объекты, например, атмосфера. Нижние слои жидкости, находящиеся под действием поля силы тяжести, испытывают дополнительное давление со стороны верхних ее слоев. Благодаря своему весу, давление несжимаемой жидкости возрастает по мере увеличения глубины погружения по следующему закону: p2 = p1 + ·g·h,     (14.2) где p1 и p2 - давление в менее и более глубоких слоях жидкости, h - разность уровней этих слоев жидкостей,  - плотность жидкости, g - ускорение свободного падения. Суммарное давление, оказываемое на жидкость внешними силами p0 и весом столба жидкости ·g·h, называется гидростатическим. Гидростатическое давление равно: p = p0 + ·g·h.     (14.3)
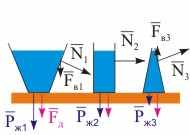Рис. 14.2. Гидростатический парадокс.	Заметим, что сила, с которой столб жидкости давит на дно Fд зависит от площади дна и высоты столба жидкости, но не зависит от формы сосуда (см. рис. 14.2) и, следовательно, может отличаться от веса жидкости Pж. Данное явление называется гидростатическим парадоксом. Он объясняется тем, что при наличии наклонных поверхностей у сосуда, существуют вертикальные составляющие силы Fв бокового давления N жидкости, действующие на эти поверхности (стенки). В случае суживающегося от земли сосуда они направлены вверх, а в случае расширяющегося сосуда - вниз.
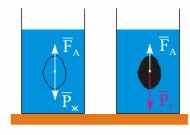Рис. 14.3. К выводу закона Архимеда.	Закон Архимеда. Наличие гидростатического давления приводит к существованию статической выталкивающей силы, действующей на погруженные в жидкость тела. Эту силу назвали силой Архимеда, а закон, определяющий ее величину,  законом Архимеда: выталкивающая сила (сила Архимеда) равна весу жидкости, объем которой совпадает с объемом погруженной в жидкость части тела. Докажем закон Архимеда. Выделим в однородной жидкости объем произвольной формы. Поскольку выделенное количество жидкости находится в равновесии, то ее вес Pж по величине равен выталкивающей силе FА, действующей на поверхность этого объема со стороны окружающей жидкости. Теперь заменим выделенную жидкость равным по объему и форме твердым телом весом Pт (см. рис. 14.3). Выталкивающая сила, обусловленная гидростатическим давлением, не изменится и по-прежнему окажется равной весу жидкости, заключенной в выделенном объеме, что доказывает справедливость закона Архимеда. Сила Архимеда направлена против действия силы тяжести, а линия ее действия проходит через центр масс объема жидкости, замещенного погруженным в нее телом, и не зависит от того, где расположен центр масс этого тела - в жидкости или вне ее. Сила Архимеда действует также на твердые тела, погруженные в газ, но ее значения из-за малой плотности газов существенно меньше веса тел и выталкивающей силы в жидкостях. Исходя из закона Архимеда можно сформулировать условие плавания тел. Если средняя плотность тела меньше, чем плотность жидкости, то часть тела выступит над поверхностью жидкости.
§ 2. Кинематическое описание движения идеальной жидкости Понятие идеальной жидкости. Метод Эйлера как способ описания течения жидкости. Линии и трубки тока. Уравнение неразрывности струи.
"Водопад". Фото Tsuenso Yamada.	Понятие идеальной жидкости. В предыдущих темах рассматривалось движение частиц и твердых тел. Характерной чертой этих физических объектов являлась их дискретность, т. е. расположение в строго определенных ограниченных и изменяющихся с течением времени, областях пространства. В противоположность этому жидкости и газы, если не вдаваться в молекулярную структуру вещества, можно рассматривать как непрерывные среды, применяя к описанию их движения характерные методы. В качестве физической модели, служащей для описания течения жидкости, используем так называемую идеальную жидкость. Идеальная жидкость - жидкость, плотность которой не зависит от давления и постоянна в любой пространственной области, а вязкость (внутреннее трение) отсутствует.
	Кинематическое описание течения жидкости. Для кинематического описания течения идеальной жидкости воспользуемся методом Эйлера. Для этого выберем систему отсчета и зададим в ней поле скоростей, т. е. зависимость скорости каждой точки среды  от ее радиус-вектора и времени  = f(r, t). Мысленно проведем в жидкости линии тока. Линии тока - линии, касательные к которым совпадают с направлением вектора скорости течения жидкости . При этом совершим построение так, чтобы густота линий тока (число линий, пронизывающих площадку единичной площади в перпендикулярном им направлении) была бы пропорциональна величине вектора скорости. Направление линий тока при этом должно совпадать с направлением . Применение метода Эйлера дает наглядное представление о направлении и величине вектора скорости течения жидкости в разных точках. В случае стационарного течения картина линий тока не изменяется, а сами они совпадают с траекториями движения молекул жидкости. Поверхность, образованная линиями тока, проведенными через все точки замкнутого контура, называется трубкой тока. При стационарном течении жидкости ее молекулы не пересекают трубку тока.
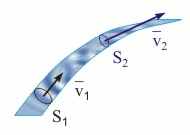Рис. 14.4. Иллюстрация течения идеальной жидкости.	Уравнение неразрывности струи. Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова (см. рис. 14.4). Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Следовательно, объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S··dt, то выполняется соотношение: S1·1 = S2·2    или S· = const.     (14.4) Выражение (14.4) называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.
§ 3. Уравнение Бернулли Стационарное течение идеальной жидкости в однородном поле силы тяжести. Вытекание жидкости из сосуда. Формула Торричелли.
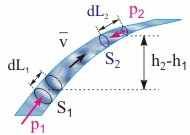Рис. 14.5. К выводу уравнения Бернулли.	Стационарное течение жидкости. Рассмотрим стационарное течение идеальной жидкости плотности  в однородном поле силы тяжести под действием сторонних сил. Пусть под действием перепада давлений p1 - p2, вызванного внешними сторонними силами, за интервал времени dt молекулы жидкости, находящиеся в сечениях трубки тока S1 и S2, сместились вдоль нее соответственно на  расстояния dL1 и dL2 (см. рис.14.5). Для описания движения воспользуемся энергетическими соображениями. Рассмотрим жидкость, сосредоточенную между сечениями трубы S1 и S2. Согласно закону изменения полной механической энергии ее приращение равно работе внешних сторонних Aст и внутренних неконсервативных сил (см. тему 7), действующих на рассматриваемый объем жидкости. Последняя из этих составляющих в отсутствие внутреннего трения у идеальной жидкости равняется нулю и, следовательно, E = Aст.     (14.5) Исходя из того, что работу совершают только тангенциальные составляющие сил, получим выражение для расчета работы по перемещению выделенного объема жидкости: Aст = p1·S1·dL1 - p2·S2·dL2.     (14.6) Из уравнения неразрывности струи (14.4) и формулы (14.6) cледует, что Aст = (p1 - p2)·dV,     (14.7) где dV - объем жидкости, протекающей через сечение трубки тока за время dt. Приращение полной механической энергии E найдем как сумму приращений кинетической и потенциальной энергий в 1-м и 2-м сечениях трубки тока: E = (·V·22/2 - ·V·12/2) + (·V·g·h2 - ·V·g·h1).     (14.8) Из выражений (14.5), (14.7) и (14.8) с учетом произвольности выбора сечений 1 и 2, получим, что для выбранной трубки тока справедливо следующее соотношение: ·2/2 + p + ·g·h = соnst.     (14.9) Соотношение (14.9), называемое уравнением Бернулли, получено для достаточно узкой трубки тока и, строго говоря, справедливо, когда трубка тока переходит в линию тока. Оно хорошо выполняется для реальных жидкостей, обладающих малым внутренним трением. Следствия из уравнения Бернулли. 1. Течение жидкости по горизонтальной трубе. В данном случае уравнение Бернулли примет вид: ·2/2 + p = соnst.     (14.10) Из выражения (14.10) следует, что в областях трубки с большей скоростью течения жидкости давление меньше. Согласно уравнению неразрывности струи скорость течения жидкости больше в местах с меньшим сечением трубы, следовательно, давление по мере перехода к более узким ее участкам уменьшается. Образующийся при этом перепад давлений заставляет жидкость двигаться вдоль трубы с ускорением. Обратите внимание, что зависимости скорости и давления от координаты вдоль оси трубы, а также направление ускорения не зависят от направления скорости течения жидкости.  2. Вытекание жидкости из сосуда. Пусть идеальная жидкость вытекает из сосуда через отверстие малого диаметра, просверленное у его дна. Все линии тока проходит через свободную поверхность, находящуюся на высоте h над дном сосуда, и отверстие, причем постоянная в уравнении Бернулли будет равна для всех линий тока. Рассмотрим одну из этих линий, учитывая, что скорость течения жидкости у свободной поверхности пренебрежимо мала по сравнению со скоростью вытекания жидкости из отверстия. Учтя вышеизложенное и применив уравнение Бернулли к линии тока на уровне свободной поверхности жидкости и отверстия получим: pатм + ·g·h = pатм +·2/2,     (14.11) где pатм - атмосферное давление;  - скорость вытекания жидкости из отверстия сосуда. Из уравнения (14.11) получим выражение для расчета скорости истечения жидкости через отверстие, называемое формулой Торричелли:  = (2·g·h)1/2.    (14.12) Скорость вытекания идеальной жидкости из отверстия в сосуде рассчитывается по той же самой формуле, что и для случая свободного падения тела с высоты h. Для реальных жидкостей скорость вытекания из отверстия будет несколько меньше.
§ 4. Вязкостные свойства жидкостей и газов Понятие вязкости и формула Ньютона. Ламинарное и турбулентное течение жидкости. Число Рейнольдса.
	Вязкостные свойства жидкостей. Идеальная жидкость является физической моделью, позволяющей понять суть явления в некотором приближении. Всем реальным жидкостям присущи вязкость или внутреннее трение, что приводит к появлению у них принципиально новых свойств. В частности, возникшее в жидкости движение после прекращения действия причин, его вызвавших, постепенно замедляется. Следовательно, жидкость при своем движении в трубе испытывает сопротивление. Такого рода сопротивление называют вязким, подчеркивая тем самым отличие от сопротивления в твердых телах. В твердых телах в случае попытки изменения их формы (например, при сдвиге одной части тела относительно другой) возникает сила упругой деформации сдвига, пропорциональная смещению атомов, находящихся в узлах кристаллической решетки соседних атомных слоев. В жидкости эта сила пропорциональна величине изменения скорости, наблюдающейся при переходе между соседними слоями взаимодействующих молекул. Рассмотрим следующий опыт. Расположим жидкость между двумя твердыми параллельными пластинами равной площади S, находящимися на расстоянии d. Попытаемся сдвинуть одну из пластин относительно другой. Опыт показывает, что для поддержания постоянной относительной скорости движения этих пластин  к одной из них нужно приложить постоянную силу F, направленную вдоль поверхности пластины и пропорциональную площади пластины S. |F| = η·||·S/d, (14.13) где η - постоянная для данной жидкости величина,  называемая вязкостью.   Необходимость наличия такой силы обусловлена “прилипанием” приграничных молекул жидкости к пластинам, что в свою очередь вызывает движение молекул, находящихся в объеме жидкости, с разной скоростью. Величина силы F зависит от свойств жидкости и обусловлена взаимодействием между проскальзывающими относительно друг друга слоями жидкости. Это взаимодействие характеризует внутреннее трение.
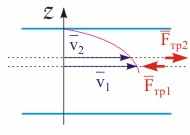Рис. 14.6. Взаимодействие молекул жидкости, расположенных в соседних слоях.	Рассмотрим взаимодействие слоев жидкости, движущихся параллельно друг другу и стенкам трубы, в которую заключена эта жидкость. На рис. 14.6 изображены соседние слои жидкости, расположенные на расстоянии Δz друг от друга. Площадь соприкасающихся слоев S существенно больше размеров молекул. Верхний и нижний слои выделенного объема движутся параллельно оси трубы и имеют разные скорости: 1 и 2 соответственно. Для сохранения постоянства этих скоростей к поверхностям выделенного объема необходимо приложить постоянные по величине силы F1 и F2, которые должны уравновесить силы внутреннего трения Fтр1 и Fтр2, действующие между соседними слоями выделенного объема жидкости. В соответствии с третьим законом Ньютона силы внутреннего трения равны по величине и противоположны по направлению, поэтому верхний слой замедляет движение нижнего, а нижний - ускоряет движение верхнего (см. рис. 14.6). Величина силы внутреннего трения задается формулой Ньютона: Fтр = η·|Δ/Δz|·S, (14.14) где η - коэффициент вязкости; |Δ/Δz| - модуль градиента скорости, показывающий, как быстро меняется величина вектора скорости  в направлении, перпендикулярном течению жидкости; S - площадь поверхности соприкасающихся слоев жидкости.
	Физический смысл коэффициента вязкости вытекает из выражения (14.14): коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади поверхности соприкасающихся слоев, при единичном градиенте скорости. В системе СИ вязкость измеряется в Па·с, а в СГС - в пуазах (Пз): 1 Па·с = 10 Пз. Коэффициент вязкости жидкости зависит от природы жидкости (в частности, ее плотности) и температуры, уменьшаясь с ростом последней по экспоненциальному закону. Для более объективного учета характера взаимодействия молекул в непрерывных средах с разной плотностью, например, в жидкостях и газах, вводят понятие кинематического коэффициента вязкости. Кинематический коэффициент вязкости равен отношению коэффициента η к плотности среды.
	Для объяснения температурной зависимости коэффициента вязкости жидкостей необходимо учесть характер теплового движения составляющих их молекул. Оно, в основном, сводится к механическим колебаниям молекул около положений равновесия, которые в отличие от таковых в твердом теле изменяются с течением времени за счет переходов молекул в соседние положения с локальным минимумом потенциальной энергии. Для того, чтобы молекула жидкости перескочила из одного временного положения равновесия в другое, она должна нарушить связи со своими соседями, то есть преодолеть потенциальный барьер высотой W. Величина W называется энергией активации. Величина, обратная вероятности разрыва связи, определяется отношением энергии активации к тепловой энергии, равной произведению постоянной Больцмана k и абсолютной температуры T. С другой стороны, молекулы жидкости большую часть времени находятся около положения равновесия, и движущаяся масса жидкости увлекает соседние слои в основном за счет сил межмолекулярного взаимодействия, которые убывают с ростом температуры, и, следовательно, вязкость также убывает с ростом температуры. Я. И. Френкель, исходя из характера теплового движения молекул в жидкостях, показал, что температурная зависимость вязкости жидкости имеет активационный характер и описывается выражением: η = C·e W/(k·T),    (14.15) где W - энергия активации; Т - абсолютная температура; C - постоянная величина; k - постоянная Больцмана, k = 1.38·10-23 Дж/К; е - основание натурального логарифма. Применяя формулу Ньютона (14.14) для решения задач, связанных с течением жидкости, можно получить определенные количественные закономерности, которые используются для экспериментального определения коэффициента вязкости. Наиболее точными и распространенными методами определения вязкости являются: метод, основанный на измерении скорости падения шарика в вязкой среде (метод Стокса);  метод, основанный на измерении средней скорости установившегося течения жидкости в капилляре (метод Пуазейля).