1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени
| Вид материала | Документы |
Содержание§ 1. Релятивистский закон преобразования скоростей и ускорений Преобразование скоростей. Преобразование ускорений. |
- А. Закон инерции, 40.83kb.
- Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
- Воробьева Валентина Константиновна курс лекций, 273.12kb.
- Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
- Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
- Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
- Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
- Линейное пространство, 700.44kb.
§ 1. Релятивистский закон преобразования скоростей и ускоренийПреобразование скоростей в релятивистском случае. | |||||
 Ускоритель заряженных частиц. Лаборатория Э. Ферми (США). Длина окружности главного кольца ускорителя 6.3 км. Фото IGDA/Fermilab. | Преобразование скоростей. Пронаблюдаем за движением частицы относительно двух различных ИСО. Пусть СО S движется относительно системы S' слева направо со скоростью V. Обозначим за и ' скорости частицы в системах S и S' соответственно и попытаемся найти связь между ними. Для этого сначала продифференцируем уравнение (15.9) из системы преобразований Лоренца: 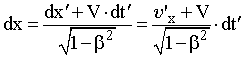 . (16.1) . (16.1)Затем разделим левую и правую части этого выражения на dt и, воспользовавшись определением мгновенной скорости, получим выражение для расчета проекции скорости частицы на ось OX в системе S. 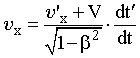 . (16.2) . (16.2)Отношение dt'/dt найдем путем дифференцирования уравнения (15.11) системы преобразований Лоренца: 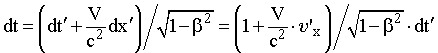 ; (16.3) ; (16.3)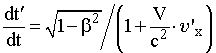 . (16.4) . (16.4)Исходя из выражений (16.2) и (16.4), получим закон преобразования проекций скоростей на ось OX при переходе от рассмотрения движения частицы в одной ИСО к рассмотрению этого движения относительно другой ИСО: 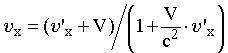 . (16.5) . (16.5)Проведя аналогичные выкладки для проекций скоростей на оси OY и OZ, получим: 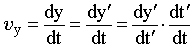 ; (16.6) ; (16.6)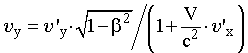 ; (16.7) ; (16.7)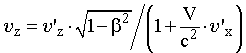 . (16.8) . (16.8)Уравнения (16.5), (16.7) и (16.8) представляют собой закон преобразования скоростей в релятивистском случае. Этот закон соответствует постулатам специальной теории относительности, а именно:
 | ||||
| | Преобразование ускорений. Пусть две произвольные ИСО движутся друг относительно друга, как в предыдущем случае, но сама частица движется с ускорением. Обозначим за a ускорение частицы в системе S, а за a' - ее ускорение в системе S'. Найдем связь между проекциями вектора ускорения на оси координат в этих ИСО. Продифференцировав уравнение (16.5), а затем разделив его на dt и учтя соотношение d'x/dt = (d'x/dt')·dt'/dt и выражение (16.4), получим следующие равенства: 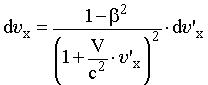 ; (16.9) ; (16.9)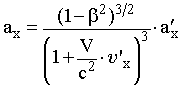 . (16.10) . (16.10)Рассмотрим частицу в тот момент времени, когда она покоится относительно системы S'. Такую систему назовем сопровождающей СО. Для этой системы вместо уравнения (16.10) получим более простое выражение: ax = (1 - β2)3/2∙a'x. (16.11) Проведя аналогичные вычисления для проекций скоростей на направления, перпендикулярные скорости движения собственной СО, можно доказать, что выполняются следующие равенства: ay = (1 - β2)1/2∙a'y, az = (1 - β2)1/2∙a'z. (16.12) Таким образом, составляющие ускорения вдоль направления движения собственной СО и в перпендикулярном ему направлении изменяются по-разному. Уравнения (16.11) и (16.12) представляют собой закон преобразования продольной и поперечной составляющих ускорения для сопровождающих СО. Из закона преобразования ускорений вытекают важные следствия:
 | ||||

