1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Вид материала

Документы

Содержание § 1. Законы изменения и сохранения импульса Механическая система, на которую не действуют внешние силы, называется замкнутой (изолированной). Закон изменения импульса системы Импульс как универсальная характеристика систем. Импульс является характеристикой состояния частиц и систем.

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 1. Законы изменения и сохранения импульса

Понятие импульса системы.
Закон изменения импульса системы.
Импульс как универсальная характеристика состояния систем.
Закон сохранения импульса.

Рис. 6.1. Распад частицы на две составляющие, произошедший в замкнутой системе

Понятие импульса системы. Вернемся к рассмотрению результата распада частицы на составляющие, произошедшего в покоящейся относительно наблюдателя замкнутой ИСО.

Механическая система, на которую не действуют внешние силы, называется замкнутой (изолированной).

Импульсом системы P называется величина, равная векторной сумме импульсов составляющих ее частиц p_i.

,     (6.1)
где N - число частиц системы.

Импульс системы является аддитивной величиной независимо от наличия взаимодействия между частицами системы и характера этого взаимодействия. Например, для системы, состоящей из двух жестко связанных тел, движущихся поступательно, скорость системы равна скорости любого из этих тел, в то время как импульс системы равен векторной сумме импульсов тел системы.

Покажем, что импульс является универсальной характеристикой, описывающей движение системы в целом. Рассмотрим сначала распад одной покоящейся относительно некоторой ИСО частицы на две составляющие, происходящий в замкнутой системе. Согласно результатам эксперимента импульсы частиц, возникших после распада, равны по величине и противоположны по направлению  p₁ = -p₂. Следовательно, импульс системы частиц после распада равен нулю:

p₁ +  p₂ = 0.    (6.2)

До распада импульс этих частиц в выбранной нами ИСО также равнялся нулю P = M·υ = 0. Таким образом, суммарный импульс рассматриваемой системы, на которую не оказывается внешнего воздействия, аддитивен и сохраняется. Для системы, состоящей из двух частиц:

P = p₁ + p₂ = const.    (6.3)

Это утверждение справедливо также, когда исходная частица в СО движется со скоростью u, отличной от нуля. Для доказательства этого положения выберем вспомогательную систему S', движущуюся с такой постоянной скоростью V, что до распада частица в ней покоилась, т. е. V = υ. В дальнейшем системы, относительно которых тело покоится, будем называть собственными СО.

Запишем закон сохранения импульса для собственной системы отсчета:

P' = m₁·υ₁' + m₂·υ₂' = M·υ' = 0.   (6.4)

Далее, используя закон преобразования скоростей (2.28), получим доказываемый результат:

m₁·(υ₁ - V) + m₂·(υ₂ - V) = 0;
P = m₁·υ₁ + m₂·υ₂ = (m₁ + m₂)·V = M·V.
     (6.5)

Если продолжить рассуждения, предположив, что одна из этих частиц вновь распадется на составляющие, то импульс этих составляющих также сохранится и окажется равен импульсу вновь выбранной частицы до распада. Следовательно, импульс системы, состоящей из трех частиц, по-прежнему останется равен импульсу исходной не распавшейся частицы. Распространяя эти рассуждения на произвольное число распадов, получим, что импульс замкнутой системы, состоящей из произвольного числа частиц, в случае их распада сохраняется.

Исходя из вышеизложенного следует, что импульс любой замкнутой системы независимо от скорости ее движения остается постоянным, но значения этих констант в разных ИСО в общем случае не равны.

Закон сохранения импульса замкнутой системы справедлив также и для случая захвата частиц. Убедимся в этом, изучив предварительно причины изменения импульса системы.






 

Закон изменения импульса системы. Рассмотрим систему, состоящую из нескольких частиц, обладающих массами m_i. Запишем закон движения, основываясь на определении импульса системы и законах движения входящих в нее частиц (4.5). Произведем векторное суммирование всех скоростей изменения импульсов частиц системы и сил, действующих на них. Выделим два типа сил: внутренние, обусловленные взаимодействием частиц системы между собой, и внешние, обусловленные воздействиями извне.

Тогда закон движения системы запишется в виде:

,     (6.6)

где F_ik - внутренние силы взаимодействия i-й и k-й частиц
системы между собой;
F_i - равнодействующая внешних сил, приложенных к i-й частице.

Согласно третьему закону Ньютона каждая пара частиц действует друг на друга с силами, равными по величине и противоположными по направлению F_ik = -F_ki. Следовательно, результирующая внутренних сил равняется нулю и

скорость изменения импульса системы P равняется векторной сумме внешних сил F_i, действующих на частицы этой системы.

.     (6.7)

Уравнение (6.7) справедливо для любого момента времени и не зависит от конкретного способа взаимодействия частиц между собой. Изменение импульса системы за конечный промежуток времени можно рассчитать, произведя суммирование импульсов внешних сил по отдельным участкам движения в соответствии с уравнением (6.8).

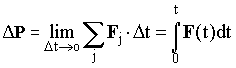.     (6.8)

Изменение импульса системы за конечный промежуток времени t равно определенному интегралу от импульса равнодействующей внешних сил.

Импульс как универсальная характеристика систем. Итак, импульс является универсальной по сравнению со скоростью физической величиной по следующим причинам:

	через понятие массы изменение импульса частицы определяют результат взаимодействия с другими частями системы;
	это аддитивная, в отличие от скорости, величина;
	величина, которая сохраняется для замкнутых систем;
	является характеристикой любых материальных объектов, в том числе имеющих массу, равную нулю (например, световых квантов).

Импульс является характеристикой состояния частиц и систем.







Рис. 6.2. Иллюстрация закона сохранения импульса при абсолютно упругом соударении шаров

Закон сохранения импульса. Из закона изменения импульса вытекают условия его сохранения:

импульс замкнутой системы или системы, для которой действие всех внешних сил скомпенсировано, сохраняется.

Отметим часто встречающиеся на практике случаи, в которых возможно применение закона сохранения импульса:

	в случае равенства нулю какой-либо из проекций результирующей внешних сил, действующих на систему, проекция импульса системы на соответствующую ось сохраняется;
	в случае ударных, взрывных воздействий на систему ее импульс сохраняется. Действительно, для кратковременного воздействия величина ∆t стремится к нулю, а величина F конечна, следовательно, произведение F·∆t стремится к нулю и импульс системы сохраняется.

Закон сохранения импульса позволяет сделать важные выводы об изменении состояния системы, не прибегая к уравнениям динамики, т. е. к знанию конкретных зависимостей силы от времени для произвольных моментов t.

Важно, что закон сохранения импульса является фундаментальным законом природы, применимым не только к описанию механического движения. Его справедливость не доказывается теоретически. Она подтверждается результатами экспериментов и выводами из частных физических законов и принципов.

В первом параграфе мы рассмотрели лишь частный случай применения этого закона в механике и его соответствие законам Ньютона.