Учебно-методический комплекс Для специальности: 080801 Прикладная информатика (в экономике) Москва 2009
| Вид материала | Учебно-методический комплекс |
Содержание7. Задания для самостоятельной работы студентов Количество рабочих мест K |
- Учебно-методический комплекс Для специальности: 080801 «Прикладная информатика (в экономике)», 357.03kb.
- Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике), 325.69kb.
- Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике), 223.84kb.
- Учебно-методический комплекс для специальности 080801 Прикладная информатика (в экономике), 639.9kb.
- Учебно-методический комплекс Для специальности: 080801 Прикладная информатика (в экономике), 575.12kb.
- Учебно-методический комплекс Для специальности: 080801 «Прикладная информатика (в экономике)», 489.66kb.
- Учебно-методическим советом экономического факультета мировые информационные ресурсы, 221.33kb.
- Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике), 278.53kb.
- Учебно-методический комплекс Для специальности 080801 Прикладная информатика (в экономике), 610.8kb.
- Учебно-методический комплекс Для специальности 080801 Прикладная информатика (в экономике), 296.07kb.
7. Задания для самостоятельной работы студентов
Тема 2. Априорный анализ компонент временного ряда
- Вопросы для самоконтроля:
- Понятия, категории и методы Общей теории статистики, используемые при статистическом моделировании и прогнозировании.
- Основные этапы разработки статистических прогнозов.
- Методы и приемы, позволяющие определить тенденцию в ряду динамики. Метод скользящей средней.
- Решить задачи:
Задача 1. На сахарном заводе один из цехов производит рафинад. Контроль качества обнаружил, что один из ста кусочков сахара разбит. Если Вы случайным образом извлекаете два кусочка сахара, то чему равна вероятность того, что, по крайней мере, один из них будет разбит? (Предполагаем независимость событий, это предположение справедливо вследствие случайности отбора).
Задача 2. Детали для обработки поступают из двух заготовительных цехов: из первого цеха – 70%, из второго – 30%, причем продукция первого цеха имеет 10% брака, а продукция второго цеха – 20% брака. Какова вероятность того, что случайно взятая деталь будет без дефектов?
Задача 3. Число яхт, сходящих со стапелей маленькой верфи – случайная величина, заданная следующим рядом распределения:
| xi | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P(X)=pi | 0,20 | 0,20 | 0,30 | 0,10 | 0,10 | 0,05 | 0,05 |
Чему равна ожидаемая средняя сумма заработка конструктора яхты, если предположить, что конструктор зарабатывает в месяц фиксированную сумму, равную 25000 условных денежных единиц плюс 5000 условных денежных единиц за каждую сошедшую со стапелей яхту?
Задача 4. Служащий рекламного агентства утверждает, что время, в течение которого телезрители помнят содержание коммерческого рекламного ролика, подчиняется экспоненциальному закону с λ=0,25 дня. Найдите долю зрителей, способных вспомнить рекламу спустя 7 дней?
Задача 5. При сборе урожая ананасов оказалось, что средний вес плода равен 650 г. Применяя неравенство Маркова, оцените вероятность того, что наудачу взятый плод имеет массу не более 750 г.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 3. Моделирование тенденции.
- Вопросы для самоконтроля:
- Методы и приемы, позволяющие определить тенденцию в ряду динамики. Метод аналитического выравнивания.
- Эталонные типы развития социально-экономических явлений во времени. Нелинейные модели и их линеаризация.
- Методы выявления тенденции средней и дисперсии. Метод Фостера-Стюарта.
- Решить задачи:
Задача 1. Вероятность того, что завтра цены на потребительские товары вырастут, равна 0,3; вероятность того, что завтра поднимется цена на серебро, равна 0,2, а вероятность одновременного роста цен на потребительские товары и серебро составляет 0,06. Являются ли цены на потребительские товары и серебро независимыми друг от друга? Поясните ответ.
Задача 2. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,67. Вероятность того, что товар будет пользоваться спросом при наличии на рынке конкурирующего товара, равна 0,42. Вероятность того, что конкурирующая фирма выпустит аналогичный товар на рынок в течение интересующего нас периода, равна 0,35. Чему равна вероятность того, что товар будет иметь успех?
Задача 3. В автомагазине ведется ежедневная запись числа продаваемых машин. Эти данные использованы для составления вероятностного распределения следующих ежедневных продаж:
-
xi
0
1
2
3
4
5
P(X)=pi
0,1
0,1
0,2
0,2
0,3
0,1
Исходя из закона распределения ежедневных продаж автомобилей, определить, чему равна ожидаемая средняя сумма заработка продавца, если предположить, что он зарабатывает сумму, которая рассчитывается приблизительно как корень квадратный из числа проданных автомобилей, умноженный на 300 условных денежных единиц.
Задача 4. Срок службы батареек для слуховых аппаратов приблизительно подчиняется экспоненциальному закону с λ=1/12. Какова доля батареек со сроком службы больше чем 9 дней?
Задача 5. Среднее значение расхода воды в населенном пункте составляет 40000 л в день. Оцените вероятность того, что в этом населенном пункте расход воды не будет превышать 115000 л в день.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 4. Моделирование периодической компоненты.
- Вопросы для самоконтроля:
- Методы выявления тенденции средней и дисперсии. Метод сравнения средних уровней.
- Классическая линейная модель множественной регрессии. Метод наименьших квадратов.
- Понятие мультиколлинеарности. Признаки и последствия мультиколлинеарности.
- Решить задачи:
Задача 1. Отдел маркетинга фирмы проводит опрос для выяснения мнений потребителей по определенному типу продуктов. Известно, что в местности, где проводятся исследования, 10% населения являются потребителями интересующего фирму продукта и могут дать ему квалифицированную оценку. Компания случайным образом отбирает 10 человек из всего населения. Чему равна вероятность того что, по крайней мере, один человек из них может квалифицированно оценить продукт?
Задача 2. Из числа авиалиний некоторого аэропорта 60% – местные, 30% – по СНГ и 10% – в дальнее зарубежье. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ таких пассажиров – 60%, на международных – 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он:
а) бизнесмен;
б) прибыл из стран СНГ по делам бизнеса;
в) прилетел местным рейсом по делам бизнеса;
г) прибывший международным рейсом бизнесмен.
Задача 3. Доход от некоторого рискованного бизнеса составляет сумму около 1000 условных денежных единиц с заданным рядом распределения:
-
xi
-2000
-1000
0
1000
2000
3000
P(X)=pi
0,1
0,1
0,2
0,2
0,3
0,1
Замечание: –2000; –1000 означают убыток.
Какой наиболее вероятностный денежный доход рискованного бизнеса?
Задача 4. Срок службы жесткого диска компьютера – случайная величина, подчиняющаяся экспоненциальному распределению со средней 12000 ч. Найдите долю жестких дисков, срок службы которых превысит 20000 ч.
Задача 5. В цехе 20 рабочих мест. Вероятности допущения брака при изготовлении однотипных деталей распределены следующим образом:
-
Количество рабочих мест Kt
2
4
6
8
pi
0.01
0,02
0,03
0,04
С каждого рабочего места случайным образом отобрано по одной детали. Определите вероятность того, что выборочная относительная частота появления бракованной детали будет отличаться от средней вероятности менее чем на 0,05.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 5. Моделирование случайной компоненты.
- Вопросы для самоконтроля:
- Понятие мультиколлинеарности. Признаки мультиколлинеарности и способы ее устранения.
- Модели связных рядов динамики. Понятие автокорреляции.
- Способы исключения автокорреляции. Коррелирование отклонений от выровненных уровней.
- Решить задачи:
Задача 1. Алмазы, возможно, вскоре станут использоваться в качестве полупроводников в спутниках связи. Теория предсказывает, что алмазные микросхемы будут более быстродействующими, термо- и радиационностойкими, что особенно важно для приборов, работающих в космосе. По оценкам экспертов, вероятности этих трех событий равны соответственно 0,9; 0,9 и 0,95. Предполагается, что обсуждение проекта по разработке алмазных микросхем стоит вести лишь в случае, если имеется хотя бы 70% уверенности в том, что они будут обладать всеми тремя указанными выше свойствами. Должен ли обсуждаться проект?
Задача 2. Исследованиями психологов установлено, что мужчины и женщины по-разному реагируют на некоторые жизненные обстоятельства. Результаты исследований показали, что 70% женщин позитивно реагируют на эти ситуации, в то время как 40% мужчин реагируют на них негативно. 15 женщин и 5 мужчин заполнили анкету, в которой отразили свое отношение к предлагаемым ситуациям. Случайно извлеченная анкета содержит негативную реакцию. Чему равна вероятность того, что её заполнял мужчина?
Задача 3. Средний годовой возврат (процент доходности) некоторой акции составляет 8,3%. Дисперсия этого возврата равна 2,3. Для другого типа акций средняя доходность составляет 8,4% в год, а дисперсия равна 6,4. Покупка какой из акций более рисковая? Почему?
Задача 4. Дневная добыча угля в некоторой шахте распределена по нормальному закону с математическим ожиданием 785 т и стандартным отклонением 60т. Найдите вероятность того что, по крайней мере, 800 т будут добыты в заданный день. Определите долю рабочих дней, в которые будет добыто от 750 до 850 т угля? Найдите вероятность того, что в данный день добыча угля упадет ниже 665 т.
Задача 5. Вероятность появлений события при каждом испытании равна 0,75. Производится 1000 независимых испытаний. Оцените вероятность того, что в этих условиях отклонений частости вероятности будет меньше, чем 0,03.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 6. Статистические методы прогнозирования динамики. Анализ тенденции, предельных и пороговых значений уровней динамических рядов. Объективизация прогнозов.
- Вопросы для самоконтроля:
- Способы исключения автокорреляции. Коррелирование последовательных разностей.
- Способы исключения автокорреляции. Метод Фриша-Воу.
- Понятие сезонных колебаний. Методы определения средних индексов сезонности.
- Решить задачи:
Задача 1. Какова вероятность того, что последняя цифра наугад набранного телефонного номера окажется равной или кратной 3?
Задача 2. Директор фирмы имеет 2 списка с фамилиями претендентов на работу. В первом списке – фамилии 5 женщин и 2 мужчин. Во втором списке оказались 2 женщины и 6 мужчин. Фамилия одного из претендентов случайно переносится из первого списка во второй. Затем фамилия одного из претендентов случайно выбирается из второго списка. Если предположить, что эта фамилия принадлежит мужчине, чему равна вероятность того, что из первого списка была извлечена фамилия женщины?
Задача 3. Число яхт, сходящих со стапелей маленькой верфи – случайная величина, заданная следующим рядом распределения:
| xi | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P(X)=pi | 0,20 | 0,20 | 0,30 | 0,10 | 0,10 | 0,05 | 0,05 |
Подсчитать ожидаемое среднее число построенных яхт, дисперсию и среднее квадратическое отклонение.
Задача 4. Для Х~N(50; 62) найдите два значения х1 и х2 симметричные относительно а=50 с Р (x1<Х< х2)=0,9.
Задача 5. Подлежат исследованию 400 проб руды. Вероятность промышленного содержания металла в каждой пробе для всех проб одинакова и равна 0,85. Используя теорему Бернулли, оцените вероятность того, что число проб с промышленным содержанием металла будет заключено между 300 и 360.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 7. Статистические методы моделирования взаимосвязи.
- Вопросы для самоконтроля:
- Модели периодических колебаний. Гармонический анализ.
- Прогнозирование рядов динамики, не имеющих тенденции.
- Прогнозирование на основе простейших методов.
- Решить задачи:
Задача 1. Вероятность того, что судоходная компания получит разрешение для захода в определенный порт назначения, зависит от того, будет принят или нет необходимый для этого закон. Компания оценивает, что вероятность того, что произойдут оба события (принят соответствующий закон и получено разрешение на посещение порта), равна 0,5, а вероятность того, что необходимый закон будет принят, равна 0,75. Предположим, что компания получила сведения, что закон принят. Чему равна вероятность того, что разрешение на заход в порт назначения будет получено?
Задача 2. Среди студентов института по результатам зимней сессии 30% первокурсников имеют только отличные оценки, среди второкурсников таких студентов 35%, на третьем и четвертом курсе их 20% и 15% соответственно. По данным деканатов известно, что на первом курсе 20% студентов сдали сессию только на отличные оценки, на втором – 30%, на третьем – 35%, на четвертом – 40% отличников. Наудачу вызванный студент оказался отличником. Чему равна вероятность того, что он (или она) – третьекурсник.
Задача 3. Число иногородних судов, прибывающих ежедневно под погрузку в определенный порт – случайная величина х, заданная так:
-
xi
0
1
2
3
4
5
P(X)=pi
0,1
0,2
0,4
0,1
0,1
0,1
Определить, чему равна вероятность того, что в какой-то определенный день число прибывающих судов превысит ожидаемое среднее.
Задача 4. Если х~N(615; 152), то найдите такое значение х, при котором Р(X<х)=0,84.
Задача 5. Принимая вероятность рождения девочки 0,52, оцените с помощью теоремы Бернулли вероятность того, что из 1000 родившихся детей мальчиков будет от 450 до 550.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 8. Статистические методы прогнозирования взаимосвязи.
- Вопросы для самоконтроля:
- Методы и приемы, позволяющие определить тенденцию в ряду динамики. Метод аналитического выравнивания экстраполяции тренда.
- Прогнозирование с учетом дисконтирования информации. Метод простого экспоненциального сглаживания.
- Прогнозирование с учетом дисконтирования информации. Метод гармонических весов. Взвешенный метод наименьших квадратов.
- Решить задачи:
Задача 1. Секрет увеличения доли определенного товара на рынке состоит в привлечении новых потребителей и их сохранении. Сохранение новых потребителей товара называется brand loyalty (приверженность потребителя к данной марке или разновидности товара), и это одна из наиболее ответственных областей рыночных исследований. Производители нового сорта товара знают, что вероятность того, что потребители сразу примут новый продукт, и создание brand loyalty потребует, по крайней мере, шести месяцев, равна 0,02. Производитель также знает, что вероятность того, что случайно отобранный потребитель примет новый сорт, равна 0,05. Предположим, что потребитель только что изменил марку товара. Какова вероятность того, что он сохранит свои предпочтения в течение шести месяцев?
Задача 2. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго автомата. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84% деталей отличного качества. Наудачу взятая, с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом? Вторым автоматом?
Задача 3. Бросаются 2 игральные кости. Пусть X – сумма выпавших очков на верхних гранях этих костей. По ряду распределения вычислить среднюю ожидаемую сумму выпавших очков, дисперсию и среднее квадратическое отклонение.
Задача 4. Найдите нормально распределенную случайную величинус математическим ожиданием -34.5 и дисперсией 9, отсекающую площадь 0,575 (справа).
Задача 5. Оцените вероятность, что при 100 подбрасываниях монеты герб появится от 450 до 550 раз?
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
Тема 9. Эвристические методы прогнозирования социально-экономических явлений.
- Вопросы для самоконтроля:
- Адаптивные методы прогнозирования. Модели полиномиального роста.
- Адаптивные модели прогнозирования с учетом сезонности.
- Эвристические методы прогнозирования. Метод Дельфи.
- Эвристические методы прогнозирования Метод мозгового штурма. Метод синектики.
- Решить задачи:
Задача 1. В большом универмаге установлен скрытый «электронный глаз» для подсчета числа входящих покупателей. Когда два покупателя входят в магазин вместе, и один идет перед другим, то первый из них будет учтен 0,98, второй – с вероятностью 0,94, оба – с вероятностью 0,93.чему равна вероятность того, что устройство сканирует по крайней мере одного из двух входящих вместе покупателей?
Задача 2. Исследователь рынка заинтересован в проведении интервью с супружескими парами для выяснения их предпочтений к некоторым видам товаров. Исследователь приходит по выбранному адресу и попадает в трехквартирный дом. По надписям на почтовых ящиках он выясняет, что в первой квартире живут двое мужчин, во второй – супружеская пара, в третьей – двое женщин. Когда исследователь поднимается по лестнице, то выясняется, что на дверях квартир нет никаких указателей. Исследователь звонит в случайно выбранную дверь, и на его звонок выходит женщина. Предположим, что если бы исследователь позвонил в дверь квартиры, где живут двое мужчин, то к двери мог подойти только мужчина; если бы он позвонил в дверь квартиры, где живут только женщины, то к двери подошла бы только женщина; если бы он позвонил в дверь супружеской пары, то мужчина или женщина имели бы равные шансы подойти к двери. Имея эту информацию, оцените вероятность того, что исследователь выбрал нужную ему дверь.
Задача 3. Процент людей, купивших новое средство от головной боли после того как увидели его рекламу по телевидению, есть случайная величина, заданная так:
-
xi
0
1
2
3
4
5
P(X)=pi
0,10
0,20
0,35
0,20
0,10
0,05
Чему равен ожидаемый процент людей, откликнувшихся на рекламу. Чему равны дисперсия и среднее квадратическое отклонение?
Задача 4. Очень наблюдательный вор, занимающийся кражей предметов искусства, который, вероятно, знает хорошо статистику, заметил, что частота, с которой охранники обходят музей, равномерно распределена между 15 и 60 мин-1. Следовательно, если X обозначает время до появления охраны (в минутах), то дифференциальная функция для X имеет вид
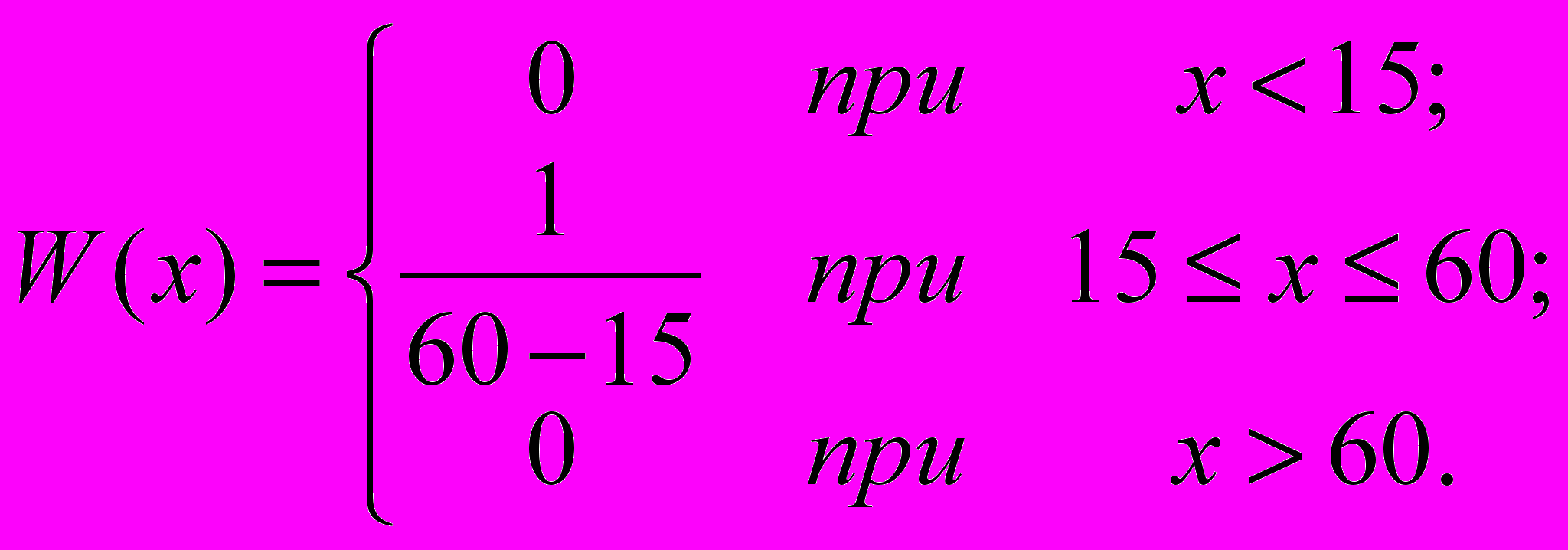
а) Постройте графики W(x:) и F(x).
б) Найдите вероятность того, что охранник появится в течение 35 мин после появления вора.
в) Найдите вероятность того, что охрана не появится в течение 30 мин.
г) Найдите вероятность того, что охрана появится между 35 и 45 мин после прихода вора.
Задача 5. Вероятность наступления некоторого события в каждом из 1000 испытаний равна 0,75. Используя теорему Бернулли, оцените вероятность того, что событие состоится число раз, заключенное между 600 и 660.
Задача 6. Составьте задачу по изученному материалу курса теории вероятностей, используя предметную область экономики. Решите задачу и приведите пояснения.
