Geum.ru

Учебно-методический комплекс Для специальности: 080801 Прикладная информатика (в экономике) Москва 2009

Вид материалаУчебно-методический комплекс

Содержание


6. Темы практических занятий
Литература: 6, 8, 15.
Подобный материал:
1   2   3   4   5   6   7

6. Темы практических занятий


Тема 2. Априорный анализ компонент временного ряда.

Задача 1. Определить показатели, характеризующие изменение уровней ряда динамики на цепной и базисной основе:
  • абсолютный прирост;
  • темп роста;
  • темп прироста;
  • средний уровень ряда;
  • средний абсолютный прирост;
  • средний темп роста;
  • средний темп прироста.

Результаты вычислений представить в табличной форме.

Таблица 1.1

Годы
2004
2005
2006
2007
2008

Добыча нефти, млн. тонн
490,8
519,7
545,8
571,5
586


Таблица 1.2

Годы
2004
2005
2006
2007
2008

Прибыль предприятия общественного питания (в сопоставимых ценах), млн. руб.
6,4
7,2
8,6
9,8
10,3


Таблица 1.3

Годы
2004
2005
2006
2007
2008

Урожайность зерновых, ц/га
18
21
20
19
17


Таблица 1.4

Валовая продукция, млн. руб.
2003
2004
2005
2006
2007
2008

в ценах 1992 г.

в ценах 1995 г.
40

-
45

-
50

54
-

58
-

65
-

68


Задача 2. Определить среднее квадратическое отклонение и коэффициент вариации.

Таблица 1.2
Январь
Февраль
Март
Апрель
Май

Численность работающих, чел.
352
367
368
409
365

в том числе совместителей, чел.
21
12
8
27
16

Фонд оплаты труда, млн. руб.
176
185
258
245
290


Литература: 1, 2, 3.


Тема 3. Моделирование тенденции.

Задача 1. Произведите анализ основной тенденции развития ряда динамики методом скользящей средней

Таблица 2.1

Годы
2003
2004
2005
2006
2007
2008

Значение показателя
12
19
26
38
46
56


Задача 2.Произведите анализ основной тенденции развития ряда динамики методом аналитического выравнивания

Таблица 2.2

Годы
2004
2005
2006
2007
2008

Значение показателя
3,4
4,2
5,6
6,8
7,3


Литература: 22, 23, 24.


Тема 4. Моделирование периодической компоненты.

Задача 1. Основная тенденция ряда динамики имеет вид 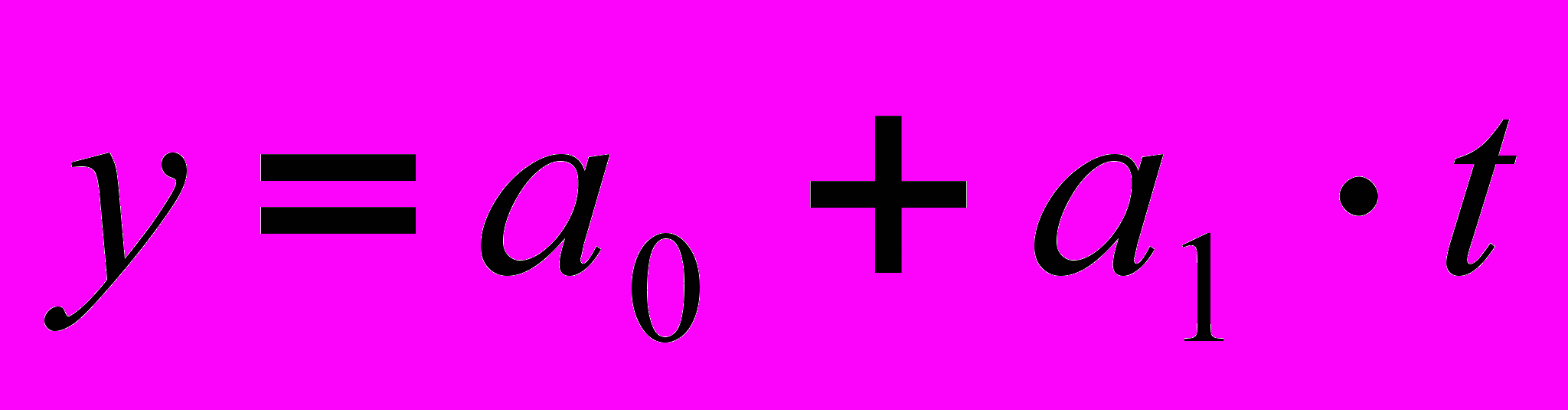. Для 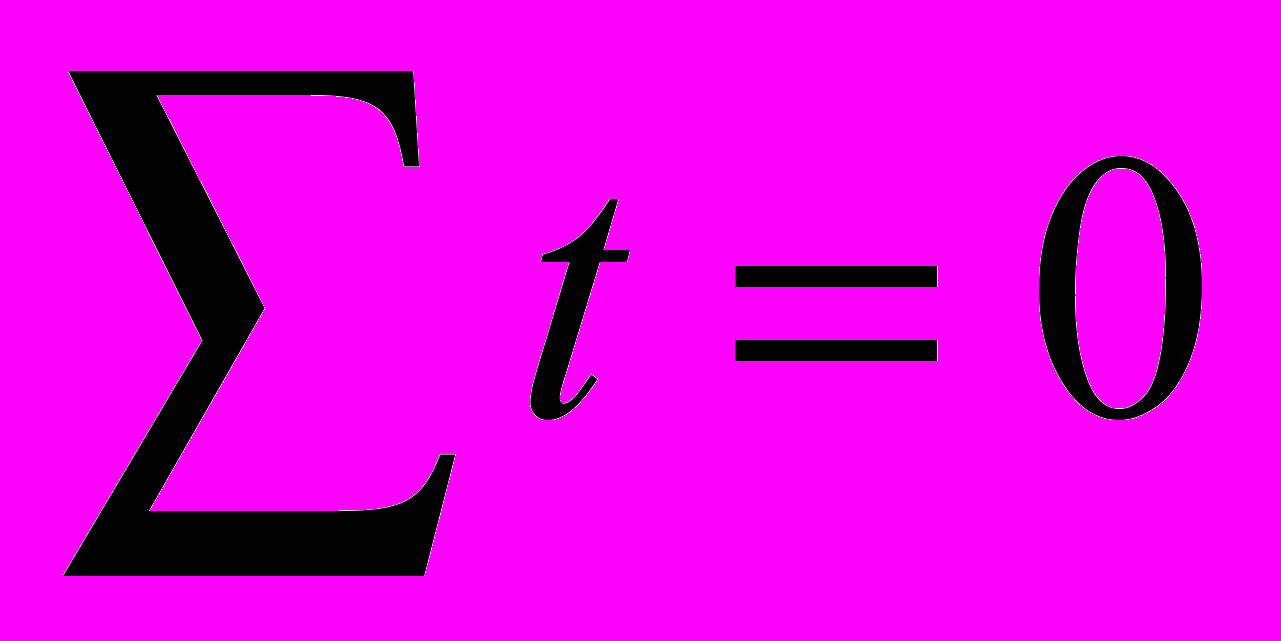параметры =11, 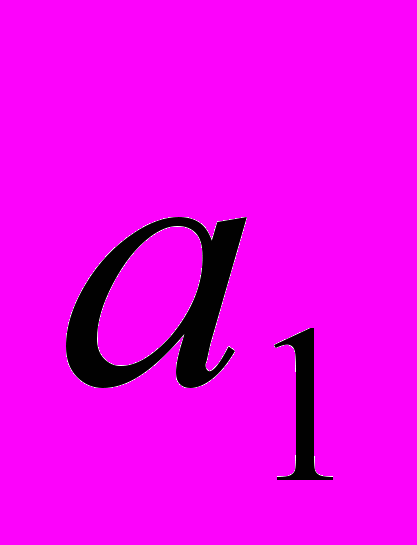= 0,7.

Определите значение показателя «Производство миксеров, тыс. штук» в 2009 году, если известно, что исходный ряд включает данные за 2003–2008 гг.

Таблица 3.1

Годы
2003
2004
2005
2006
2007
2008

Значение показателя
12
19
26
38
46
56


Задача 2.Определите наличие тенденции в средней и в дисперсии методом Фостера-Стюарта.


Таблица 3.2

Годы
2004
2005
2006
2007
2008

Значение показателя
19
20
18
21
20


Задача 3.Определите наличие тенденции в средней и в дисперсии методом сравнения средних уровней ряда.

Таблица 3.3

Годы
2004
2005
2006
2007
2008

Валовой выпуск (в сопоставимых ценах, млн. руб.)
133
156
124
171
183


Задача 4.Рассчитайте коэффициент автокорреляции между соседними уровнями ряда динамики по данным таблиц 3.1, 3.2, 3.3.


Задача 5.Определите значение показателя Y – производство бумаги, млн. тонн в 2009 г. на основе линейной функции и на основе параболы 2-ого порядка. Оцените точность полученных данных. Выберите наиболее адекватную модель для прогноза.

Таблица 3.5

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Y
3,2
3,7
4,0
4,2
4,3
4,3
4,0
4,1
5,0
5,3


Задача 6.Проверьте следующие данные о работе хозрасчетного предприятия на наличие автокорреляции:

Таблица 3.6

Годы
2003
2004
2005
2006
2007
2008

Стоимость основных фондов,

млн. руб.
21,5
18,4
21,1
20,4
19,2
23,3

Прибыль, млн. руб.
3,8
3,6
4,1
4,4
4,6
5,4


Задача 7.Проверьте гипотезу о наличии тенденции в средней ряда динамики Y (розничный товарооборот области, млн. руб.) по месяцам года, всеми известными Вам методами:

Таблица 3.7

Месяцы
1
2
3
4
5
6
7
8
9
10
11
12

Y
7,4
7,9
8,7
8,2
7,9
8,2
8,8
8,7
8,7
8,1
8,3
9,0

Литература: 5, 11, 18.

Тема 5. Моделирование случайной компоненты.

Задача 1. По данным о среднедневной реализации молочной продукции вычислить индексы сезонных колебаний и построить график сезонной волны.

Таблица 4.1

Кварталы
2004
2005
2006
2007

I
39.9
38.1
40.9
50.7

II
65.8
82.3
96.5
110.6

III
63.9
83.4
98.8
116.7

IV
38.5
45.1
58.8
60.5


Таблица 4.2

Кварталы
2004
2005
2006
2007

I
40.1
39.5
38.7
36.5

II
55.8
54.7
56.1
59.8

III
62.4
60.8
62.8
64.7

IV
53.7
52.1
53.4
50.2


Задача 2. По данным табл. 4.1 постройте аддитивную и мультипликативную модели. Выберите наиболее адекватную модель.


Задача 3. Для построения модели внутригодовой динамики произвести обработку исходных данных методом первой гармоники ряда Фурье. Исходные и расчетные данные нанести на график, сделать выводы.


Таблица 4.3

Месяцы
1
2
3
4
5
6
7
8
9
10
11
12

Объём товаро-оборота, млн. руб.
27.3
28
32.1
30.1
29.2
30
30.1
32
31.4
32.3
32.1
33.5


Литература: 4, 8, 19.


Тема 6. Статистические методы прогнозирования динамики. Анализ тенденции, предельных и пороговых значений уровней динамических рядов. Объективизация прогнозов.

Задача 1. Рассчитайте коэффициент автокорреляции остаточных величин ряда динамики.

Таблица 5.1

Год
2003
2004
2005
2006
2007
2008

Исходные уровни
3,4
4,2
5,6
6,8
7,3
8,1

Выровненные уровни
3,5
4,1
5,4
6,8
7,4
8,2


Задача 2. Рассчитайте коэффициент автокорреляции связных рядов динамики на основе коррелирования отклонений от выровненных уровней ряда динамики.

Таблица 5.2

dx
0,1
0,2
0,1
0
-0,1
-0,3

dy

-0,2
-0,1
-0,1
0
0
0,4

Задача 3. Рассчитайте коэффициент корреляции связных рядов динамики (x – поголовье коров, голов; y – производство молока, тонн) на основе коррелирования последовательных разностей уровней.

Таблица 5.3

x
4
5
8
7
6
8
10

y
10
12
14
10
11
15
18


Задача 4. По следующим данным постройте линейную регрессионную модель на основе метода пользовательских разностей:

Таблица 5.4

Год
2000
2001
2002
2003
2004
2005
2006
2007
2008

Материальные затраты, млн. руб.
1.4
1.5
1.6
1.8
2.2
2.3
2.6
2.8
3.0

Прибыль, млн. руб.
0.8
0.9
1.0.
1.0
1.1
1.2
1.4
1.6
1.7

Задача 5. По следующим данным (x – стоимость основных фондов, млрд. руб.; y – стоимость текущего ремонта, млрд. руб.) постройте регрессионную модель динамики методом Фриша-Воу.

Таблица 5.5

Год
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

x
1.3
2.7
2.0
2.3
2.4
2.9
3.1
3.5
3.8
4.0

y
26
24
30
27
33
35
41
51
53
62


Литература: 6, 8, 15.