Geum.ru

Учебно-методический комплекс Для специальности: 080801 Прикладная информатика (в экономике) Москва 2009

Вид материалаУчебно-методический комплекс
Подобный материал:
1   2   3   4   5   6   7
Тема 7. Статистические методы моделирования взаимосвязи.

Задача 1. Построить прогноз по ряду динамики урожайности картофеля одной из областей на основе распределения Пуассона.

Таблица 6.1

Год
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Урожайность, ц/га
121
102
134
140
146
102
114
128
104
123

Задача 2. Построить прогноз по ряду динамики урожайности зерновых и оценить вероятность того, что в 2009 гг. значения уровней будут выше, чем в 2003 г.

Таблица 6.2

Год
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Урожайность, ц/га
18
19
17
20
21
20
22
16
20
19


Задача 3. Построить прогноз по ряду динамики среднего числа отказов оборудования в смену одного из цехов завода, используя распределение Пуассона.


Таблица 6.3

Месяц
январь

2008
февраль

2008
март

2008
апрель

2008
май

2008
июнь

2008
июль

2008

Число отказов, единиц
16,8
26
19,1
27,3
22,5
20,1
19,3




Месяц
август

2008
сентябрь

2008
октябрь

2008
ноябрь

2008
декабрь

2008
январь

2009
февраль

2009

Число отказов, единиц
18,7
19,4
7,6
18,2
21,7
20,4
19,3


Задача 4. Построить точечный прогноз по ряду динамики производства минеральных удобрений двумя методами.

Таблица 6.4

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Производство,

млн. тонн

усл. ед.
15,9
17,4
19,4
22,0
22,6
23,5
23,7
24,8
26,0
27,3


Задача 5. Построить интервальный прогноз по ряду динамики производства продукции (в стоимостном выражении) двумя методами.

Таблица 6.5

Годы
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Производство,

млн. руб.
13
15
16
17
19
22
23
24
25
27
26



Задача 6. Сделайте интервальный прогноз величины грузооборота транспортного управления на 2008 год методом среднего абсолютного прироста и среднего темпа роста.

Таблица 6.6

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007

Грузооборот,

млн.т./км
89
99
102
111
119
126
133
141
150


Задача 7. Постройте прогноз численности населения города N до 2009 года на основе двух методов, если известно, что в 1999 году численность населения составляла 5,4 млн. человек, а в 2004 году – 8,9 млн. человек.


Задача 8. Сделать интервальный прогноз по линейному тренду на 2005 год по следующим данным о производстве целлюлозы:

Таблица 6.7

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Производство,

млн. тонн
6,1
6,3
6,8
7,2
7,4
7,6
7,0
7,1
7,3
7,4

Известно, что 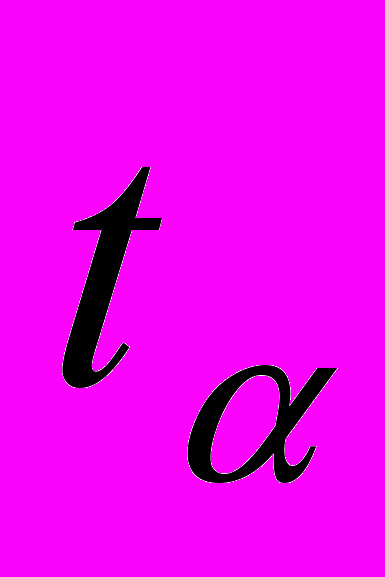= 2,631.


Задача 9. Сделать интервальный прогноз расхода дизельного топлива по всем видам автомобильных перевозок на 2009 год на основании следующих данных:

Таблица 6.8

Годы
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Расход,

млн. тонн
81
86
93
101
109
115
124
130
138
147
151


Задача 10. По следующим данным о выплавке стали с применением кислорода (млн. тонн) построить прогноз на основе кривой Перля–Рида на 2009 год. Определить коэффициент несоответствия.

Таблица 6.9

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007

Значения

показателя
107
108
107
115
116
117
122
124
127


Задача 11. По следующим данным о выплавке чугуна с применением природного газа (млн. тонн) построить прогноз на основе кривой Гомперца на 2009 год. Определить коэффициент несоответствия.

Таблица 6.10

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007

Значения

показателя
86,0
90,7
99,9
99,4
102,2
102,8
102,9
105,8
106,3


Задача 12. Сделать интервальный прогноз на 2005 год по следующим данным о производстве бумаги (табл.6.11). Метод прогнозирования выбрать самостоятельно. Обосновать выбор.

Таблица 6.11

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Производство,

млн. тонн
4,8
4,9
5,1
5,3
5,4
5,4
5,1
5,2
5,3
5,3


Задача 13. По следующим данным о производстве продукции (млн. руб.) построить прогноз на 2009 год на основе кривой Перля-Рида:


Таблица 6.12

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Показатель
72
85
89
90
92
102
103
103
106
107


Задача 14. По следующим данным о численности младших научных сотрудников (тыс. чел.) построить прогноз методом простого экспоненциального сглаживания на 2009 год:

Таблица 6.13

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007

Показатель
45,0
42,0
40,2
40,6
42,0
40,8
39,7
38,7
34,9


Задача 15. По следующим данным о численности старших научных сотрудников (тыс. чел.) построить точечный прогноз методом гармонических весов на 2009 год:

Таблица 6.14

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Показатель
53
66
69
71
74
75
78
77
80
81


Задача 16. По следующим данным о численности докторов наук (тыс. чел.) построить прогноз методом простого экспоненциального сглаживания на 2009 год:

Таблица 6.15

Годы
1999
2000
2001
2002
2003
2004
2005
2006
2007

Показатель
37,7
38,7
39,7
41,0
42,7
44,3
45,7
47,4
49,7


Задача 17. По приведенным данным о реализованной продукции отрасли произвести прогнозирование на 2008–2010 гг. методом экспоненциального сглаживания.

Таблица 6.16

Годы
2001
2002
2003
2004
2005
2006
2007

Объем реализованной

продукции (млн. руб.)
284,3
269,5
311,4
333,5
348,9
371,4
369,2




Годы
1999
2000
2001
2002
2003
2004

Объем реализованной

продукции (млн. руб.)
394,0
429,8
466,7
458,1
492,3
509,6


Задача 18. По приведенным данным о выпуске продукции произвести прогноз на 2009-2011 гг. на основе метода гармонических весов.

Таблица 6.17

Годы
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008

Выпуск

продукции

(млн. руб.)
311,4
333,5
348,9
371,4
368,2
394,0
429,8
466,7
458,1
492,3
509,6


Литература: 7, 15, 17.


Тема 8. Статистические методы прогнозирования взаимосвязи.

Задача 1. По данным, представленным в таблице ниже, изучается зависимость объема валового национального продукта Y (млрд. долл.) от следующих переменных: X1- потребление, млрд. долл., X2- инвестиции, млрд. долл.

Таблица 7.1
1
2
3
4
5
6
7
8
9
10

Y
14
16
18
20
23
23,5
25
26,5
28,5
30,5

X1
8
9,5
11
12
13
14
15
16,5
17
18

X2
1,65
1,8
2,0
2,1
2,2
2,4
2,65
2,85
3,2
3,55



  1. Рассчитайте коэффициенты линейной модели множественной регрессии: Y = b0 + b1∙X1 + b2∙X2 + ε.
  2. Оцените адекватность и точность построенного уравнения регрессии по значениям коэффициента детерминации R2, F-критерия Фишера и средней относительной ошибки аппроксимации.


Задача 2. В таблице приведены исходные данные Y и расчетные значения 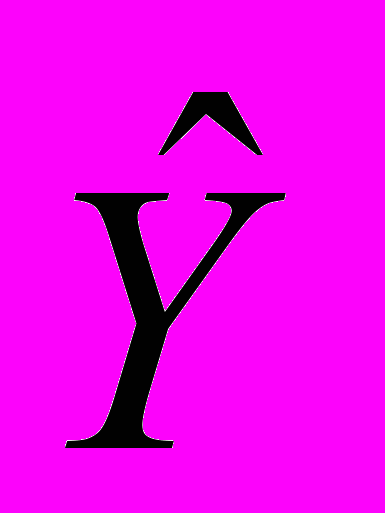, полученные по линейной модели множественной регрессии:
Y = 123,35 + 0,53∙X1 - 9,89∙X2 + ε.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Y
20
25
30
45
60
69
75
90
105
110
120
130
130
130
135
140



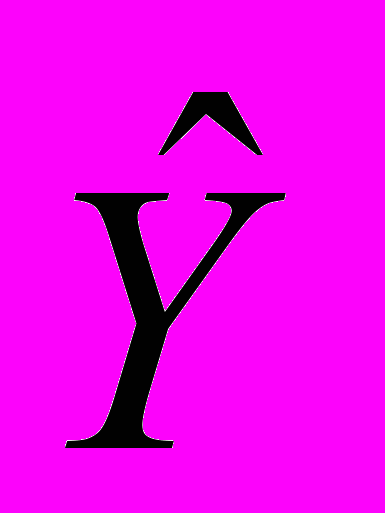9,9
32,3
44,8
47,5
46,3
63,7
86,6
102,2
103,8
102,8
120,0
131,9
124,6
122,6
137,1
137,8



  1. По имеющимся данным заполните таблицу дисперсионного анализа.
  2. Оцените адекватность построенного уравнения регрессии по значениям коэффициента детерминации R2, критерия Фишера F.
  3. Оцените точность модели по значению средней относительной ошибки аппроксимации.


Задача 3. По результатам одинакового количества наблюдений построены два уравнения регрессии:

Y = 0,72 + 1,63∙X1 + ε R2 = 0,9878; R2adj = 0,9863

(0,88) (0,06)


Y = 0,70 + 1,46∙X1 + 0,90∙X2 + ε R2 = 0,9885; R2adj = 0,9852

(0,91) (0,26) (1,42)

В скобках указаны значения стандартных ошибок коэффициентов.
  1. Вычислите расчетные значения t-статистики для коэффициентов.
  2. По указанным значениям R2 и R2adj, а также по вычисленным значениям t-статистики для коэффициентов сделайте вывод о целесообразности включения в модель фактора X2.


Задача 4. В таблице ниже представлены результаты регрессионного анализа для уравнения зависимости оборота розничной торговли (Y, млрд. руб.) от трех факторов: Х1 - денежные доходы населения, млрд. руб.; Х2 – численность безработных, млн. чел.; Х3 – официальный курс рубля по отношению к доллару США.
Коэффициенты
Стандартная ошибка
t-статистика
P-
Значение
Нижние 95%
Верхние 95%

Y-пересечение
55,73586
?
3,086061
0,005826
18,0623
93,40942

X1
?
0,034007
9,744398
4,88E-09
0,26044
0,402314

X2
-4,97938
2,048365
?
0,024592
-9,25219
-0,70657

X3
2,382175
?
8,374001
5,71E-08
1,788776
2,975575


Известны следующие статистические характеристики рядов динамики:
Y
Х1
Х2
Х3

Среднее значение
114,30
185,81
8,93
17,39

Дисперсия
1351,24
3426,01
0,4167
71,57



  1. Восстановите пропущенные значения.
  2. Проверьте гипотезы: Н0: b1=0; b2=0; b3=0.
  3. Запишите уравнение регрессии. Верно ли утверждение: "Численность безработных оказывает наибольшее влияние на объем розничной торговли, так как коэффициент при факторе Х2 имеет наибольшее значение по модулю"?
  4. Рассчитайте стандартизованные коэффициенты модели. Запишите уравнение регрессии в стандартизованной форме.
  5. Ранжируйте факторы по силе воздействия на результат.


Задача 5. Изучается зависимость оборота розничной торговли (Y, млрд. руб.) от ряда факторов: 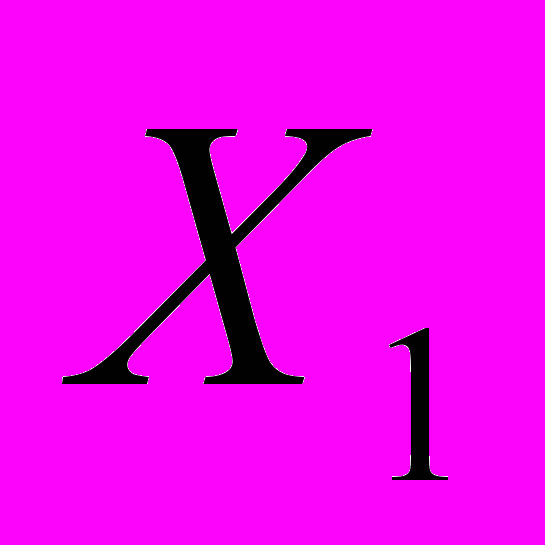- товарные запасы в фактических ценах, млрд. руб.; Х2 – номинальная заработная плата, руб.; Х3 – денежные доходы населения, млрд. руб.; Х4 – официальный курс рубля по отношению к доллару США.

По данным за 18 месяцев было построено следующее уравнение регрессии:

Y = 8,075 + 0,711X1 – 0,006X2 + 0,233X3 + 1,967X4 + ε R2 = 0,9864

(0,63) (1,52) (-0,34) (2,10) (5,50)


Затем были добавлены наблюдения еще за 6 месяцев и получено новое уравнение регрессии:

Y = -14,638 + 1,010X1 + 0,006X2 + 0,237X3 + 1,646X4 + ε R2 = 0,9893

(-1,51) (2,38) (0,52) (4,36) (7,37)


В скобках указаны расчетные значения t-критерия Стьюдента для коэффициентов.
  1. Как можно объяснить значительное изменение коэффициентов регрессии, а также изменение знака коэффициента при факторе X2?
  2. Что можно предпринять, чтобы получить адекватную модель оборота розничной торговли?


Задача 6. Предполагается, что объем предложения некоторого блага Y для функционирующей в условиях конкуренции фирмы зависит линейно от цены X1 этого блага и заработной платы X2 сотрудников этой фирмы. Исходные данные за 16 месяцев представлены в таблице ниже:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Y
20
25
30
45
60
69
75
90
105
110
120
130
130
130
135
140

X1
10
15
20
25
4
37
43
35
38
55
50
35
40
55
45
65

X2
12
10
9
9
8
8
6
4
4
5
3
1
2
3
1
2



    1. Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
    2. Дайте экономическую интерпретацию параметров модели.


Литература: 1, 12, 16.


Тема 9. Эвристические методы прогнозирования социально-экономических явлений.

Задача 1. Изучается зависимость объема ВВП (Y, млрд. долл.) от уровня прибыли в экономике (Хt, млрд. долл.). Получена следующая модель с распределенными лагами:

Yt = -5 + 1,5∙Xt + 2∙Xt-1 + 4∙Xt-2 + 2,5∙Xt-3 + 2∙Xt-4 + εt.

(2,2) (2,3) (2,5) (2,3) (2,4)

В скобках указаны значения t-критерия Стьюдента для коэффициентов регрессии. R2 = 0,9.
  1. Проанализируйте полученные результаты регрессионного анализа.
  2. Дайте интерпретацию параметров модели: определите краткосрочный и долгосрочный мультипликаторы.
  3. Определите величину среднего лага и медианного лага.


Задача 2. По данным о динамике товарооборота (Y, млрд. руб.) и дохода населения (X, млрд. руб.) была получена следующая модель с распределенными лагами:

Yt = 0,55∙Xt + 0,25∙Xt-1 + 0,14∙Xt-2 + 0,09∙Xt-3 + εt.

(0,06) (0,04) (0,04) (0,03)

В скобках указаны значения стандартных ошибок для коэффициентов регрессии. Значение R2 = 0,99.
  1. Проанализируйте полученные результаты регрессионного анализа.
  2. Дайте интерпретацию параметров модели: определите краткосрочный и долгосрочный мультипликаторы.
  3. Определите величину среднего лага и медианного лага.


Литература: 1, 2, 3.