Geum.ru

Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике) Москва 2009

Вид материалаУчебно-методический комплекс

Содержание


1. Цель, задачи и предмет дисциплины 5
3. Объем дисциплины 8
5. Темы практических занятий 13
Цель, задачи и предмет дисциплины
Требования к уровню освоения дисциплины
Инновационные технологии, используемые в преподавании дисциплины
Обучение он-лайн.
ОБЪЕМ ДИСЦИПЛИНЫ Объем дисциплины и виды учебной работы
Распределение часов по темам и видам учебной работы
Содержание курса
Тема 2. Нелинейное программирование. Динамическое программирование
Тема 4. Решающее правило Байеса, страхование
Тема 6. Однопродуктовая макромодель оптимального развития экономики
Темы практических занятий
Задания для самостоятельной работы студентов
Тема 1. Введение. Линейное программирование. Симплекс-метод. Транспортные задачи.
Тема 6. Однопродуктовая макромодель оптимального развития экономики.
Вопросы для подготовки к зачету
8. УЧЕБНО-МЕТОДИМЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ 8.1.Литература
8.2. Методическое обеспечение дисциплины
...
Полное содержание
Подобный материал:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ
ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
(РГТЭУ)


Кафедра информационных технологий и телекоммуникаций


Одобрено учебно-методическим советом

факультета социальных и

информационных технологий


МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА


Учебно-методический комплекс


Специальность: 080801 Прикладная информатика (в экономике)


Москва 2009


Автор-составитель: канд. физ.-мат. наук Л.И. Коровина


Учебно-методический комплекс «Математическая экономика» составлен в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования по специальности 080801 «Прикладная информатика (в экономике)

Дисциплина входит в федеральный компонент цикла дисциплин области применения и является обязательной для изучения.


©Российский государственный торгово-экономический университет, 2009


С О Д Е Р Ж А Н И Е


^ 1. ЦЕЛЬ, ЗАДАЧИ И ПРЕДМЕТ ДИСЦИПЛИНЫ 5

2. ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ 6

2.1.Инновационные технологии, используемые в преподавании дисциплины 6

^ 3. ОБЪЕМ ДИСЦИПЛИНЫ 8

3.1.Объем дисциплины и виды учебной работы 8

3.2. Распределение часов по темам и видам учебной работы 9

4. СОДЕРЖАНИЕ КУРСА 10

^ 5. ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ 13

6. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ 15

7. ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ 26

8. УЧЕБНО-МЕТОДИМЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ 32

8.1.Литература 33

8.2. Методическое обеспечение дисциплины 33

8.3. Материально-техническое и информационное обеспечение дисциплин 34

8.4. Интернет-источники 34

МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА 35



  1. ^

    ЦЕЛЬ, ЗАДАЧИ И ПРЕДМЕТ ДИСЦИПЛИНЫ



Актуальность изучения дисциплины "Математическая экономика" обусловлена необходимостью формирования у будущих специалистов представления о методах изучения основных процессов, протекающих в экономике современного общества, и обучения студентов применению в исследовательской деятельности современных инструментальных компьютерных средств и специального программного обеспечения.

Предполагается, что все практические занятия по данной дисциплине проводятся в компьютерных классах, оснащенных количеством ПЭВМ, равным числу студентов, и соответствующим программным обеспечением.

Целью дисциплины является подготовка студентов в области математического моделирования классических экономических задач микро- и макроэкономики, задач оптимизации и математического программирования, задач актуарной математики

Задачей дисциплины является формирование у студентов общего представления о методах математического моделирования экономических процессов с применением современных информационных технологий, а также выработка практических навыков работы с современными программными средствами, применяемыми при решении типичных проблем, возникающих в практической деятельности.


  1. ^

    ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ



Дисциплина "Математическая экономика" изучается студентами специальности 080801 «Прикладная информатика (в экономике)» на четвёртом курсе. При этом существенно используются знания и умения, приобретенные студентами при освоении дисциплин "Информатика", "Прикладная математика" и "Программные средства офисного назначения". Следует отметить, что дисциплина " Математическая экономика" предполагает при её изучении активное использование студентами современных интегрированных офисных, математических и статистических пакетов Microsoft Excel, Mathcad, Maple и Statistica..

В результате изучения дисциплины студент должен:

- иметь представление об основных методах построения математических моделей экономических задач;

- знать задачи предметной области и методы их решения с учётом традиционно сложившихся критериев классификации математических моделей экономики;

- уметь ставить и решать типичные задачи прикладной информатики;

- приобрести навыки выбора соответствующих информационных технологий, владеть ими на высоком уровне, иметь опыт работы в современных интегрированных математических средах.

    1. ^

      Инновационные технологии, используемые в преподавании дисциплины



Аппаратное обеспечение компьютерного интерфейса - группа технических средств, состоящая из вычислительной машины и периферийных устройств (предполагается, что данная технология используется при изучении всех тем).

Дискуссия – форма учебной работы, в рамках которой студенты высказывают свое мнение по проблеме, заданной преподавателем

(данная технология наиболее эффективна при проведении занятий по темам №№ 1,2,5 и при обсуждении промежуточных и итоговых результатов).

Тренинг – форма интерактивного обучения, целью которого является развитие компетентности межличностного и профессионального поведения в общении (данная технология наиболее эффективна при проведении занятий по теме 5 ).

^ Обучение он-лайн. Способ организации процесса самостоятельного изучения учебных материалов в режиме реального времени с использованием образовательной среды, основанной на сетевых (Интернет) технологиях (данная технология наиболее эффективна при проведении занятий по темам 1 и 2 с использованием указанных в УМК Интернет-источников).


  1. ^

    ОБЪЕМ ДИСЦИПЛИНЫ




    1. Объем дисциплины и виды учебной работы





Вид учебной работы
Количество часов по формам обучения




Очная
Очно-заочная

№№ семестров
7
7

Аудиторные занятия:
51
34

лекции
26
18

практические и семинарские занятия
25
16

Самостоятельная работа
49
66

Всего часов на дисциплину
100
100

Текущий контроль

(количество, №№ семестров)
2 собеседования,

7 семестр
Одно собеседование,

7 семестр

Виды итогового контроля

(экзамен, зачет)

- №№ семестров
Зачет, 7 семестр
Зачет, 7 семестр



    1. ^

      Распределение часов по темам и видам учебной работы



Форма обучения очная

Названия разделов и тем
Всего часов по учебному плану
Виды учебных занятий

Аудиторные занятия, из них
Самостоятельная работа

лекции
Практ. занятия, семинары

Раздел 1. Математическое программирование в экономике.

1. Линейное программирование. Симплекс-метод. Транспортные задачи.
19
4
5
10

2. Нелинейное программирование. Динамическое программирование.
17
2
6
9

Раздел 2. Риски и их измерители. Актуарий.

3. Риски и их измерители. Функция полезности дохода. Рыночный портфель
10
4
0
6

4. Решающее правило Байеса. Страхование.
4
2
0
2

Раздел 3. Основы моделирования управленческих решение в экономике.

5. Оптимизационные модели экономической динамики.
14
4
6
4

6. Однопродуктовая макромодель оптимального развития экономики.
6
2
0
4

Раздел 4. Финансовая математика.

7. Наращение и дисконтирование.
14
4
4
6

8. Кредитные расчёты. Оценка инвестиционных процессов
16
4
4
8

ИТОГО:
100
26
25
49



  1. ^

    СОДЕРЖАНИЕ КУРСА



Раздел 1. Математическое программирование в экономике.


Тема 1. Введение. Линейное программирование. Симплекс-метод. Транспортные задачи

Основные понятия и термины, относящиеся к математической экономике. Значимость метода линейного программирования для решения практических задач экономики, область его применения. Метод разрешающих множителей Канторовича (1938 г.) для решения экономических задач: "задача о раскрое", "транспортная задача", "задача о смеси". Симплекс-метод (Данциг, 1947 г.) - численный метод решения задач линейного программирования. Основная идея этих методов. Метод потенциала (1947 г.). Симплекс-метод как основа программного обеспечения в математических пакетах Mathcad, Maple и в надстройке "Поиск решения" пакета Microsoft Excel для решения задач линейного программирования. Основные элементы последовательности (шаги, части процесса) построения и решения компьютерной модели. Организация и схема экономико-математического моделирования. Классификация математических моделей и пакеты прикладных программ (ППП), их реализующие. Примеры применения метода линейного программирования в задачах экономики.


^ Тема 2. Нелинейное программирование. Динамическое программирование

Постановка общей задачи нелинейного программирования. Терема существования оптимального решения на множестве планов либо в граничной, либо в стационарной, либо в изолированной точке множества. Обзор инструментальных программных средств. Примеры экономических систем, меняющих свои состояния с течением времени. Постановка задачи поиска оптимального управления системой при дополнительных ограничениях. Набор процедур, архитектура пакетов, интерфейс пользователя, работа с данными, графические возможности, подготовка отчетов. Место ППП в программном обеспечении. Спектр возможных операций.


Раздел 2. Риски и их измерители. Актуарий


Тема 3. Риски и их измерители. Функция полезности дохода. Рыночный портфель

Риски и их измерители. Функция полезности дохода. Снижение риска. Модель задачи оптимизации рискового портфеля. Задача об эффективном портфеле с безрисковой компонентой. Инвестирование в два фонда. Рыночный портфель.


^ Тема 4. Решающее правило Байеса, страхование

Решающее правило Байеса. Единовременная рисковая премия, распределённый риск, комбинированное страхование, рисковая надбавка, комплексное решение основных актуарных задач. Объединение распределённых рисков. Элементы теории полезности. Страхование.


Раздел 3. Основы моделирования управленческих решение в экономике


Тема 5. Оптимизационные модели экономической динамики

Основы моделирования управленческих решений в экономике. Математическая модель оптимальных управляемых процессов. Общие постановки задачи оптимального управления для непрерывных и дискретных процессов, их сравнительный анализ. Компьютерные технологии решения оптимизационных задач управления. Обзор задач, методов и пакетов приложений интегрированных математических сред. Понятие о численных методах, лежащих в основе компьютерной реализации процесса принятия оптимизационных решений в задачах управления.


^ Тема 6. Однопродуктовая макромодель оптимального развития экономики

Однопродуктовая макромодель оптимального развития экономики. Оптимизация распределения капитальных вложений между предприятиями методом динамического программирования.


Раздел 4. Финансовая математика.


Тема 7. Наращение и дисконтирование

Наращение и дисконтирование. Эквивалентные процентные ставки. Эффективная ставка. Учёт инфляции.

Тема 8. Кредитные расчёты. Оценка инвестиционных процессов.

Финансовая эквивалентность обязательств. Кредитные расчёты: равные процентные выплаты; погашение долга равными суммами; равные срочные выплаты; формирование фонда. Оценка инвестиционных процессов: чистый приведённый доход; рентабельность; срок окупаемости; внутренняя норма доходности; показатель приведённых затрат.


  1. ^

    ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ



Раздел 1. Математическое программирование в экономике.


Тема 1. Введение. Линейное программирование. Симплекс-метод. Транспортные задачи

Вопросы к теме:

1. Решение задач экономики методом линейного программирования в среде Maple.

2. Решение задач экономики методом линейного программирования в среде Mathcad.

3. Решение задач экономики методом линейного программирования в пакете Excel.

Литература: [4, 5, 6, 7, 8, 10].


Тема 2. Нелинейное программирование. Динамическое программирование.

Вопросы к теме:

1. Решение задач экономики методом нелинейного программирования в пакете Excel.

2. Какие можно отметить особенности применения к практическим задачам экономики надстройки "Поиск решения" пакета Excel?

3. Равновесная цена. Паутинообразная модель.

Литература: [4, 5, 6, 7, 8].


Раздел 3. Основы моделирования управленческих решение в экономике.


Тема 5. Оптимизационные модели экономической динамики

Вопросы к теме:
  1. Примеры экономических систем, меняющих свои состояния с течением времени.
  2. Постановка задачи поиска оптимального управления системой при дополнительных ограничениях.

Литература: [5, 6, 8, 10].


Раздел 4. Финансовая математика.


Темы 7-8. Наращение и дисконтирование. Кредитные расчёты. Оценка инвестиционных процессов

Вопросы к теме:
  1. Наращение и дисконтирование. Эквивалентные процентные ставки. Эффективная ставка. Учёт инфляции. Финансовая эквивалентность обязательств.
  2. Кредитные расчёты: равные процентные выплаты. Погашение долга равными суммами; равные срочные выплаты; формирование фонда.
  3. Оценка инвестиционных процессов: чистый приведённый доход; рентабельность; срок окупаемости; внутренняя норма доходности; показатель приведённых затрат.

Литература: [1, 4, 9].


  1. ^

    ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ



Самостоятельная работа студентов должна соответствовать более глубокому усвоению изучаемого курса, формировать навыки исследовательской работы и ориентировать студентов на умение применять теоретические знания на практике. Задания для самостоятельной работы предполагают проработку учебного материала (по конспектам лекций, учебной и научной литературе) Самостоятельная работа должна носить систематический характер. Результаты самостоятельной работы контролируются преподавателем и учитываются при аттестации студента (зачет). При этом проводится экспресс-опрос на практических занятиях.

^ Тема 1. Введение. Линейное программирование. Симплекс-метод. Транспортные задачи.

Задача1. Требуется минимизировать затраты на перевозку товаров от предприятий- производителей на торговые склады , изменяя объемы перевозок между каждым заводом и складом , в соответствии с потребностями складов. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей. Решите задачу методами оптимизации пакета EXCEL с помощью надстройки "Поиск решения".

Рассмотрите ситуацию, когда имеется три завода: в Белоруссии, на Урале и на Украине с производственными возможностями 310, 260 и 280 стоимостных единиц соответственно, и пять региональных складов: в Казани, Риге, Воронеже, Курске и в Москве с потребностями 180, 80, 200, 160 и 220 соответственно.

Товары могут доставляться с любого завода на любой склад. Но очевидно, что стоимость доставки на большее расстояние будет больше. Пусть затраты на перевозку от завода к складу заданы таблицей:
Казань
Рига
Воронеж
Курск
Москва

Белоруссия
10
8
6
5
4

Урал
6
5
4
3
6

Украина
3
4
5
5
9


Решение задачи. Заполняем электронную таблицу.
  1. Объединяем ячейки первой и второй строки столбцов от A до G и пишем заголовок: "Транспортная задача".
  2. В шестой строке объединяем ячейки столбцов от A до G и записываем - Число перевозок от завода к складу.
  3. В седьмой строке записываем: A7 - Заводы, B7 - Всего, C7 - Казань, D7 - Рига, E7 - Воронеж, F7 - Курск, G7 - Москва.
  4. В восьмой строке записываем: A8 - Белоруссия, B8 набираем формулу =СУММ(C8:G8), продолжаем эту формулу на ячейки B9 и B10, заполняем C8:G8 - 1.
  5. В девятой строке пишем: A9 - Урал, C9:G9 - 1.
  6. В десятой строке записываем: A10 – Украина, C10:G10 – 1.
  7. Одиннадцатую строку пропускаем.
  8. В двенадцатой строке записываем: A12 – Итого, B12 пропускаем, C12 набираем формулу =СУММ(C8:C10), продолжаем эту формулу направо до столбца G включительно.
  9. Тринадцатую строку пропускаем.
  10. В четырнадцатой строке набираем: объединяем A14 с B14 и пишем - Потребности складов, C14 - 180, D14 - 80, E14 - 200, F14 - 160, G14 - 220.
  11. Обводим рамкой таблицу A6:G14.
  12. В пятнадцатой строке набираем: A15 – Заводы, B15 – Поставки, C15:G15 объединяем и пишем - Затраты на перевозку от завода к складу.
  13. В шестнадцатой строке набираем: A16 - Белоруссия, B16 – 310, C16 – 10, D16 – 8 , E16 – 6 , F16 – 5, G10 - 4.
  14. В семнадцатой строке набираем: A17 – Урал, B17 – 260+0.5*N, C17 – 6, D17 – 5, E17 – 4, F17 – 3, G17 - 6.
  15. В восемнадцатой строке набираем: A18 - Украина, B18 - 280, C18 – 3, D18 – 4, E18 – 5, F18 – 5, G18 - 9
  16. Девятнадцатую строку пропускаем.
  17. В двадцатой строке набираем: A20 - Перевозка, B20 набираем формулу =СУММ(C20:G20), C20 набираем формулу =C8*C16 + C9*C17 + C10*C18, продолжаем эту формулу направо до столбца G включительно.

Цель - уменьшение всех транспортных расходов. Изменяемые данные - объемы перевозок от каждого из заводов к каждому складу. Ограничения: количества перевезённых грузов не могут превышать производственных возможностей заводов; количество доставляемых грузов не должно быть меньше потребностей складов; число перевозок не может быть отрицательным.

Оптимизационная задача решается аналогично задачам из задания 6.

Обратите только внимание на то, что задача линейная и целочисленная.


Задача 2. Решите задачу линейного программирования в среде Maple.

Найдите минимум целевой функции f(x,y) = ax+by при заданных ограничениях:

a = 2; b = 5, x + y >= 4, x + 2y <=12, 2x + y <=12, x>=0, y>=0 .

> restart;

> with(simplex):

Warning, the protected names maximize and minimize have been redefined and unprotected


> with(plots):

Warning, the names changecoords and display have been redefined


> c1:=x+y>=4;



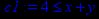
> c2:= x + 2*y<=12;



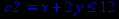
> c3:=2*x + y <=12;



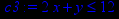
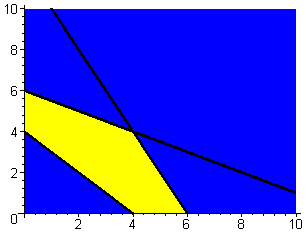
> inequal({c1,c2,c3}, x=0..10,y=0..10, optionsexcluded=(color=blue,thickness=2),

optionsfeasible=(color=yellow),

optionsclosed=(color=black, thickness=3));



> Y:=2*x+5*y;



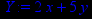
> PY:=minimize(Y, {c1,c2,c3,x>=0,y>=0});



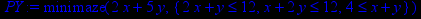
Задача имеет единственное решение.

Минимум целевой функции достигается в точке пересечения прямых у = 0 и x + y = 4.

> Ymin=2*4+5*0;



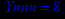
Ответ: Минимальное значение целевой функции равно 8,

достигается в точке x = 4 y = 0. Ymin = Y(4,0) = 8.

Литература: [4, 5, 6, 10].


Тема 2. Нелинейное программирование. Динамическое программирование.

Задача. Динамические системы в экономических задачах.

Исследуйте динамику популяций на примере задачи Коши для

уравнений Вольтерра - Лотка.

Предположим, что имеются две популяции - жертв и хищников. Введём обозначения: x1(t) - количество жертв в момент времени t, x2(t) - количество хищников. Пусть коэффициент a есть относительная скорость размножения жертв в отсутствие хищников, (-bx2) - уменьшение этой скорости от потерь из-за хищников, коэффициент (-с) - относительная cкорость изменения числа хищников в отсутствие пищи.

Тогда простейшей математической моделью динамической системы, описывающей изменение численности двух конкурирующих популяций во времени, является задача Коши для системы двух дифференциальных уравнений:

x1'=(a-b*x2)x1 , x2'=(-c+d*x1)x2

с начальными условиями: x1(t0)- начальное значение количества жертв, x2(t0)- хищников,

Найдём решение задачи при конкретном выборе постоянных, построим графики решения , фазовые портреты и поле направлений динамической системы в пакете Maple..

> restart;

> with(DEtools):

> a:=3.5;b:=2;c:=1.9;d:=1.1;









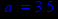
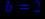
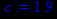
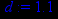
> sys1:=diff(x1(t),t)=(a-b*x2(t))*x1(t),diff(x2(t),t)=(-c+d*x1(t))*x2(t);



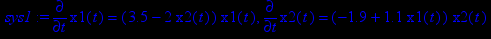
> Fnc:={x1(t),x2(t)};



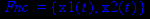
Найдём решение задачи методом Рунге-Кутта (установлен по умолчанию).

> F1:=dsolve({sys1,x1(0)=4,x2(0)=2},Fnc,type=numeric);



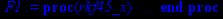
Проверим работу программы:

> F1(3);



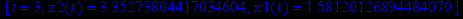
В пакете расширенной графики plots построим графики решений.

> with(plots):

Warning, the name changecoords has been redefined


> odeplot(F1,[[t,x1(t)],[t,x2(t)]],0..10,numpoints=150,thickness=2);



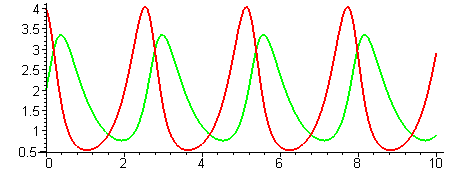
> odeplot(F1, [t,x1(t),x2(t)],0..10,numpoints=150, color=black,thickness=2);



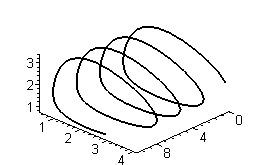
Решения имеют колебательный характер. Построим далее фазовый портрет.

> odeplot(F1,[x1(t),x2(t)],0..10,numpoints=150,color=blue,thickness=2);



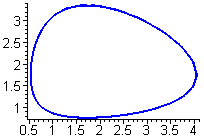
Построим поле направлений.

> dfieldplot([diff(x1(t),t)=(a-b*x2(t))*x1(t),diff(x2(t),t)=(-c+d*x1(t))*x2(t)], \

[x1(t),x2(t)],t=0..10,x1=1..5,x2=1.25..3,arrows=MEDIUM,title=`Lotka-Volterra model`,color=[(a-b*x2(t))*x1(t),(-c+d*x1(t))*x2(t),0.1]);




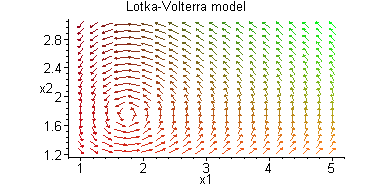
> phaseportrait([diff(x1(t),t)=(a-b*x2(t))*x1(t),diff(x2(t),t)=(-c+d*x1(t))*x2(t)], \

[x1(t),x2(t)],t=0..10,[[x1(0)=4,x2(0)=2]],stepsize=.05, \

scene=[x1(t),x2(t)],color=black,method=classical[foreuler]);




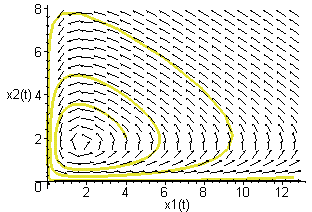
Литература: [5, 6, 7, 10].


Тема 3. Риски и их измерители. Функция полезности дохода. Рыночный портфель.

В пакете Mathcad постройте графики функции полезности и производственной функции (см. [5],п. 5.1.).


Производственные функции





















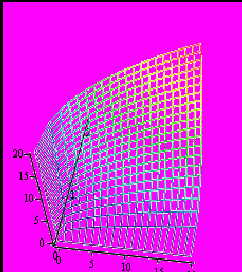
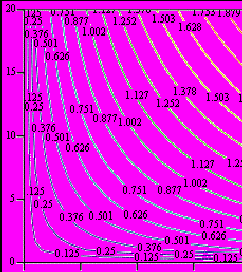
Литература: [5, 6].


Тема 4. Решающее правило Байеса, страхование.

Проработать вопросы:
  • экономическая сущность страхования,
  • виды рисков и их классификация,
  • методы оценки риска.

Литература: [1, 5].


Тема 5. Оптимизационные модели экономической динамики.

Решите задачу максимизации потребления (см. [5], п. 6.8.).































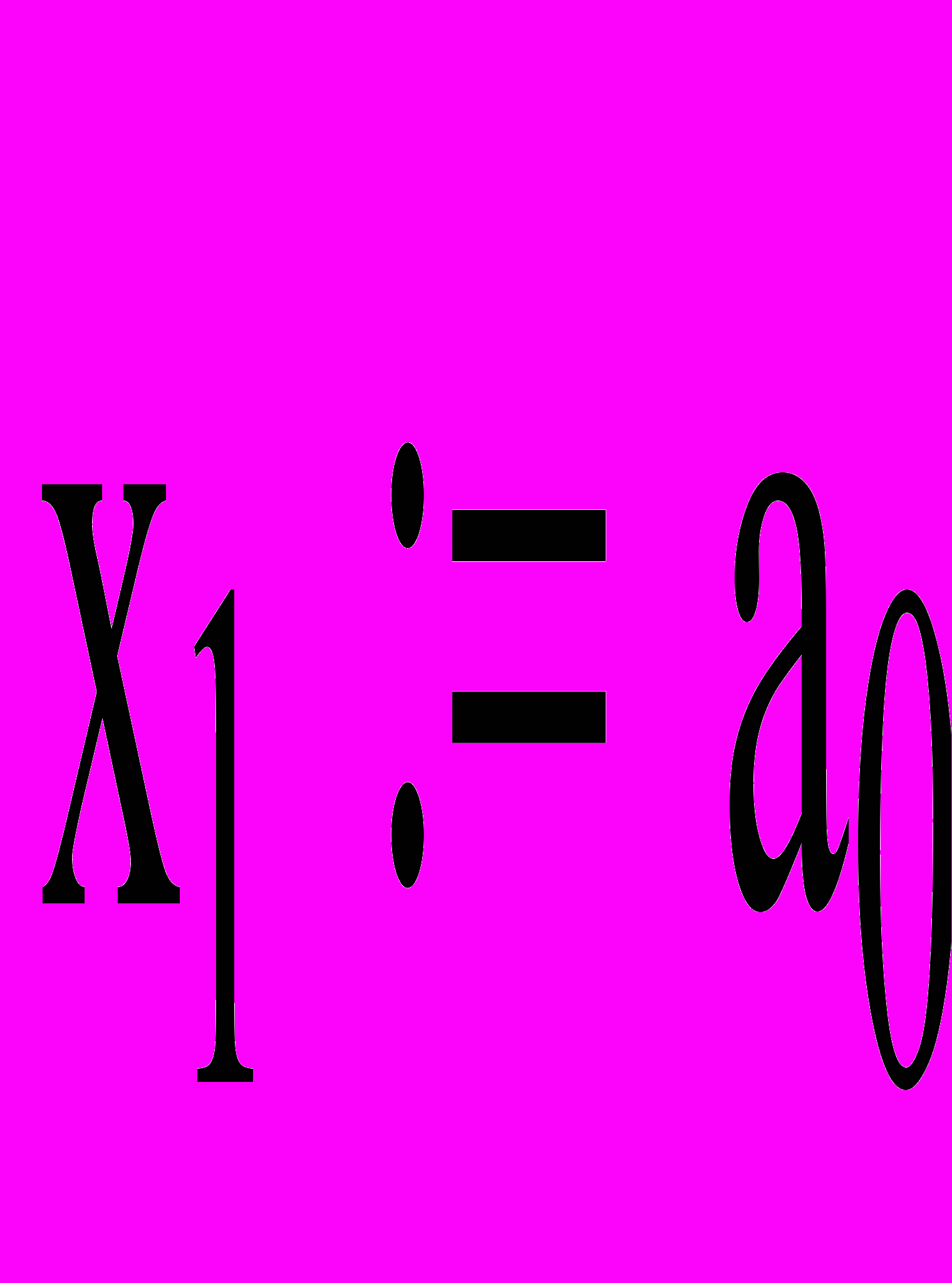
Рост капитала Сопряженная переменная




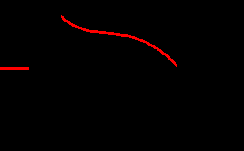
Оптимальное 




























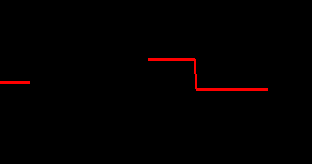
K1,K2- рост капитала в статике и в динамике

s1,s2- изменение потребления в статике и в динамике




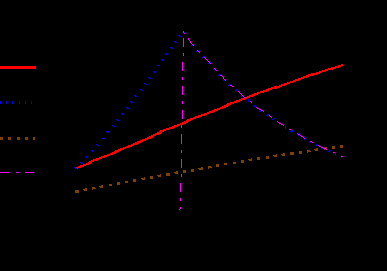
Литература: [5].


^ Тема 6. Однопродуктовая макромодель оптимального развития экономики.


Задача. Решите в пакете Mathcad задачу о динамике трёхсекторной экономики - производство средств производства, производство предметов потребления и "производство" культурных ценностей.

Указание. Воспользуйтесь постановкой задачи и образцом её решения ( см. [5], п. 6.3).


Динамика несвязанных секторов экономики


















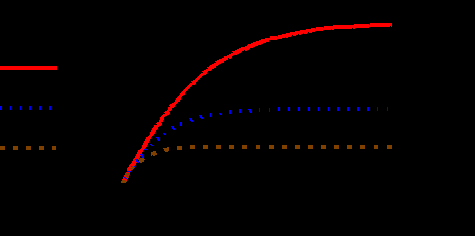
Величина капитала в конце периода по секторам


Величина дохода в конце периода по секторам


Суммарный доход


Расходы на капитализацию по секторам и в целом






Потребление по секторам и в целом

Литература: [5].


Тема 7. Наращение и дисконтирование.

Задача 1. Является ли приемлемым вложение 40000 р., при котором ежегодно возвращается 10000 в течение следующих пяти лет?

Задача 2. Принесёт ли чистую прибыль вложение 250000 р. при барьерной ставке 12% , которое обещает принести убыток в размере 55000 р. в конце первого года, но затем дать прибыль 95000 р., 140000 р. и 185000 р. в конце второго, третьего и четвёртого года соответственно?

Задача 3. Предположим, что Вы открыли счёт под 11% годовых и планируете вносить на счёт по 20000 в начале каждого года. Какая сумма окажется на Вашем счёте через 35 лет?

Литература: [9].


Тема 8. Кредитные расчёты. Оценка инвестиционных процессов.

Задача 1. Предположим, что Вы хотите взять 25-летнюю ссуду в 1 млн.р. под закладную. Если считать, что процентная ставка составляет 8% годовых, то какова будет величина Ваших месячных выплат?

Указание. Чтобы определить месячную ставку и число периодов в месяцах процентную ставку 8% следует разделить на 12 месяцев и умножить 12 на 25 лет.

Задача 2. Предположим, что Вы согласились совершить покупку за 120000 р. В течение следующих пяти лет Вы ожидаете получить от неё 25000 р.,37000 р. 35000 р., 38000 р. и40000 р. чистого рентного дохода. Можно ли рассматривать данную покупку как хорошее вложение, если барьерная ставка составляет 10%?

Указание. Вычислите внутреннюю скорость оборота.

Литература: [9].


  1. ^

    ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ




  1. Какие задачи относятся к задачам математического программирования?
  2. В чём отличие задач линейного программирования от задач нелинейного программирования?
  3. Какие задачи относятся к задачам динамического программирования? Приведите пример.
  4. Перечислите основные этапы построения компьютерной модели.
  5. Возможны ли символьные операции в пакете Mathcad?
  6. Как получить справку о возможных операциях в пакете

Mathcad?
  1. Как получить справку о возможных операциях в пакете

Maple?
  1. Как производится обработка экономической информации в пакетах Excel и Access?

9. Как включить в текстовый отчет Microsoft Word документы, созданные в пакетах Excel, Access, Mathcad, Maple?

10. Как выполнить исследование функций спроса и предложения в пакете Mathcad.?
  1. Как можно определить равновесную цену при заданных функциях спроса и предложения средствами пакета Mathcad.?
  1. Как можно найти область эластичности экономических функций средствами пакета Mathcad.?
  2. Построение однофакторных моделей Торнквиста зависимости спроса от дохода средствами пакета Mathcad.
  3. Как можно решить задачу о максимальной прибыли при заданных функциях дохода и постоянных издержек средствами пакета Mathcad.
  4. Решение задачи линейного программирования в пакете Maple. Использование функции inequal для графической иллюстрации области принятия решения.
  5. Каковы основные возможности надстройки Excel «Поиск решения»?
  6. Решение транспортной задачи в надстройке "Поиск решения" пакета Excel.
  7. Оптимизация управления оборотным капталом в надстройке "Поиск решения" пакета Excel.
  8. Простейшие приемы прогнозирования деятельности предприятия с помощью интерполяционных сплайнов в пакете Maple.
  9. Математические модели задач микроэкономики.

Найдите в среде Mathcad максимальное значение для прибыли

(X) = XP(X) - (Cf + CvX),

при заданной функции спроса P(X)= - X2 + 10X,

где X- количество товара, реализованного по цене P,

при постоянных издержках Cf= 70, и переменных издержках Cv=0.7

(затраты на производство единицы продукции).
  1. Математические модели задач микроэкономики.

Для заданной функции спроса вида:

P(Q)= -081Q2 + 0.9Q + 0.5

найдите в среде Mathcad

-эластичность спроса по цене, постройте график;

-функцию суммарного дохода, постройте график;

-найдите значение Q, при котором модуль эластичности равен единице; вычислите соответствующее значение цены.
  1. Постройте график зависимости спроса от цены товара в среде Mathcad. Найдите графически приближенно и затем численно равновесную цену товара.

Пусть функции спроса и предложения имеют вид:

D(X)= -5X + 180,

S(X)= 0.25X2 + 0.6X +80 ;

выполните в среде Mathcad следующие операции:

постройте кривую спроса P=D(X) и кривую предложения P=S(X) в зависимости от количества товара X, соответственно, приобретенного потребителем по цене P и предложенного для продажи по цене P;

определите графически координаты точки равновесия, укажите область, где предложение превышает спрос;

вычислите аналитически равновесную цену.
  1. Постройте зависимость спроса от дохода для товаров второй необходимости в рамках модели Торнквиста :

D2(x) = [α *(х- γ])]/[ x+ β]

Пусть α =7, β =2, γ=1. Определите графически, при каких значениях дохода х значения спроса D2(x) превышают значение 6.
  1. Линейное программирование.

Требуется минимизировать затраты на перевозку товаров от предприятий-производителей на торговые склады, изменяя объемы перевозок между каждым заводом и складом, в соответствии с потребностями складов. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей.

Решите задачу методами оптимизации пакета EXCEL в режиме "Поиск решения" на примере файла Solvsamp.xls, в который внесите следующие изенения:.

Потребности складов: Казань 80, Рига 20, Воронеж 170, Курск 140, Москва 200.

Поставки: Урал 180, Украина 150.
  1. Математическое программирование.

Решите методами оптимизации пакета EXCEL в режиме "Поиск решения" задачу по управлению оборотным капиталом с целью получения максимальной прибыли при сохранении достаточного резерва для покрытия расходов на примере файла Solvsamp.xls, в который внесите следующие изменения:.
  1. Начальная сумма 500 000;
  2. Расходы в 1-м месяце 80 000, в 4-м месяце 60 000.

Цель - получение наибольшего дохода по процентам.

Изменяемые данные - сумма по каждому типу депозита.

Ограничения - сумма каждого депозита не может быть меньше нуля,

конечная сумма не должна быть меньше 100 000 р.

26. Математические модели экономики. Решите задачу прогнозирования деятельности предприятия.

Прибыль предприятия в млн. руб.по месяцам отражена в таблице:


X
Янв.
Февр.
Март
Апрель
Май
Июнь
Июль

Y
27
34
45
56
64
60
56


Постройте в среде MAPLE методом наименьших квадратов многочлен третьего порядка, приближающий заданную таблицей функцию Y(X).

Вычислите приближенно прогнозируемое значение функции Y(X) в июле месяце.

Рекомендация. Время рекомендуется задавать в долях года, а для прибыли ввести масштаб 1:10.


27. Математические модели экономики. Пусть доходы предприятия по неделям зафиксированы в следующей таблице:

X
1нед.
2нед.
3нед.
5нед.
6нед.
8нед.
11нед.
12нед.

Y
1.1
1.7
2.4
1.8
1.6
1.9
1.8
2.2


Постройте в среде MAPLE кубический сплайн для табличной функции Y(X). Вычислите прогнозируемое значение дохода предприятия на 13 неделю.
  1. Математические модели микроэкономики. Рассмотрите функции Торнквиста зависимости спроса D на малоценные товары от дохода x :

D(x) = [α*х*(x+β)]/[x^2+ γ]

Пусть α=8, β=2. Подберите приближенно значение параметра γ так, чтобы максимальное значение спроса D(x) было не менее 19.
  1. Организация и схема экономико-математического моделирования.
  2. Классификация математических моделей экономики.
  3. Балансовые модели. В чём отличие модели открытого типе от модели закрытого типа?
  4. Сформулируйте основную идею балансовой модели Леонтьева. Какова область применения зтой модели?
  5. Приведите простейшую модель международной торговли. Какова область применения зтой модели?
  6. Какие экономические зависимости описывает производственная функция? Какой вид имеет производственная функция Кобба-Дугласа?
  7. Модель задачи оптимизации рискового портфеля.
  8. Функция полезности дохода. Снижение риска.
  9. Какие методы применяются для оптимизации распределения капитальных вложений между предприятиями?
  10. Какова основная идея метода половинного деления вычисления корней нелинейного уравнения в задачах экономики?
  11. Какова основная идея метода Ньютона вычисления корней нелинейного уравнения в задачах экономики?
  12. Какие вычислительные задачи называются плохо обусловленными? Чем может быть вызвана большая величина интервала неопределённости корня при решении нелинейного уравнения?
  13. Наращение и дисконтирование. Эквивалентные процентные ставки.
  14. Простейшие приемы прогнозирования экономической деятельности с помощью интерполяционных сплайнов в пакете Maple.



  1. Постройте зависимость спроса D1 от дохода x для товаров первой необходимости в рамках модели Торнквиста :

Dl(x) = [α*х]/[x+β]

Пусть α =8, β =2.5. Определите графически, при каких значениях дохода х значения спроса Dl(x) начинают отличаться от предельного значения меньше, чем на 4 ?
  1. Динамические системы в экономических задачах. Моделирование динамики цен.
  2. Динамические системы в экономических задачах. Моделирование системы "хищник - жертва". Уравнения Вольтерра - Лотка.
  3. Прогнозирование в среде STATISTICA . Классические модели временных рядов.
  4. Прогнозирование в среде STATISTICA . Экспоненциальное сглаживание.
  5. Перечислите финансовые функции пакета Excel для анализа инвестиций.
  6. Вычисление текущей стоимости ряда равных по величине периодических выплат.
  7. Вычисление текущей стоимости единовременной выплаты.
  8. Чистая текущая стоимость как типичный метод определения выгодности вложения.
  9. Вычисление будущей величины вложения.
  10. Кредитные расчёты: равные процентные выплаты.
  11. Вычисление размера периодической выплаты, необходимой для погашения ссуды за определённое число периодов.
  12. Вычисление платежей по процентам за заданный период при постоянных периодических выплатах и постоянной процентной ставке.
  13. Вычисление числа периодов, необходимых для погашения ссуды при заданной величине периодических выплат.
  14. Перечислите финансовые функции пакета Excel для анализа скорости оборота вложения.
  15. Вычисление скорости оборота вложения по ряду постоянных периодических выплат.
  16. Вычисление скорости оборота вложения по единовременной выплате.
  17. Вычисление внутренней скорости оборота вложения.
  18. Перечислите финансовые функции пакета Excel для вычисления амортизации.
  19. Можно ли рассматривать производственную функцию как математическую модель, описывающую зависимость объема продажи от величины ресурсов различного вида? Почему?
  20. Методы оптимизации в пакетах приложений интегрированных математических сред.



^

8. УЧЕБНО-МЕТОДИМЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ




8.1.Литература



Основная

1. Грищенко Н.Б. Основы страховой деятельности: учеб.пособие.-

М.: Финансы и статистика, 2008 - 352с.

2. Дьяконов В.П. Maple 9.5/10 в математике, физике и образова

нии -М.:СОЛОН-Пресс, 2006 - 720 с. ил. - (Серия "Библиоте-

ка профессионала").

3. Кирьянов Д.В.Matcad 14-СПб.:БХВ-Петебург,2007.-704с.:ил. + Видеокурс (на CD-ROM).
  1. Красс М.С. Математика в экономике. Математические методы и модели: учебник / М.С. Красс, Б.П. Чупрынов. - М.: Финансы и статистика, 2007.-544 с.
  2. Охорзин В.А. Оптимизация экономических систем. Примеры и алгоритмы в среде Mathcad: Учеб.пособие. -М.: Финансы и статистика,2005.-144 с.
  3. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. Математика в экономике: Учебник: В 2-х ч. Ч.1,Ч.2 / А.С. - 2-е изд. перераб. и доп. - М.: Финансы и статистика, 2004. - 944 с.

Дополнительная

7. Альсевич В.В. Введение в математическую экономику. Конструктивная теория. Учеб.пособие, 2-е изд., Изд.ЛКИ, 2007, 256 с.

8. Аттетков А.В. Введение в методы оптимизации: учеб. пособие / А.В. Аттетков, В.С. Зарубин, А.Н. Канатников. - М.: Финансы и статистика; ИНФРА-М, 2008. -272 с.

9. Веденеева Е.А. Функции и формулы Excel 2007. Библиотека пользователя. - СПб.: Питер, 2008. - 384 с.
  1. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров: Учебное пособие.- М.: Финансы и статистика, 2003-656с.



^

8.2. Методическое обеспечение дисциплины




    1. Коровина Л.И. Вычислительная математика для экономистов. Учебное пособие. М.: Изд-во МГУК, 2000, 44 с.
    2. УМК " Математичксеая экономика".- М.: РГТЭУ, 2009 г.



^

8.3. Материально-техническое и информационное обеспечение дисциплин



Класс ПЭВМ не ниже Intel Pentium 64 Mb RAM, 2GB HDD с установленным программным обеспечением: Microsoft Windows XP, Microsoft Windows 2000 Professional, Microsoft Office XP, Microsoft Office 2003, математические интегрированные пакеты прикладных программ Mathcad, Maple Statistica; офисный пакет Microsoft Excel; применяются по мере надобности.

8.4. Интернет-источники



Актуальная информация по интегрированным пакетам прикладных программ и возможностям их использования:
  • www.maplesoft.com;
  • www.mathcad.com;
  • www.exponenta.ru.



МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА




Учебно-методический комплекс


В авторской редакции

Компьютерная верстка А.С. Новоженовой


Подписано в печать 16.02.2009 г. Формат 60х84/8. Бумага офсетная.

Гарнитура Times New Roman. Объем 4,25 п.л. Тираж 100 экз.

Цена договорная. Изд. зак. № 146. Тип. зак. №

Издательство Российского государственного торгово-экономического университета
ул. Смольная, 36, г. Москва, А-445, ГСП-3, 125993