Учебно-методический комплекс по дисциплине «Анализ данных и прогнозирование экономики» для студентов специальностей: «Экономика» Астана 2010
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс по дисциплине: «анализ проектов» для студентов специальностей, 2311.99kb.
- Учебно-методический комплекс для студентов по дисциплине «оценка бизнеса и инноваций», 4385.11kb.
- Учебно-методический комплекс дисциплины: Прогнозирование национальной экономики Специальность, 345.29kb.
- Учебно-методический комплекс по дисциплине «Экономика и управление в акционерных обществах», 610.54kb.
- Учебно-методический комплекс по дисциплине «Инвестиционная деятельность предприятия», 593.61kb.
- Учебно-методический комплекс по дисциплине «финансы» астана, 2010, 1311.57kb.
- Учебно-методический комплекс по дисциплине «Институциональная экономика» Для специальности:, 1370.37kb.
- Учебно-методический комплекс по дисциплине теневая экономика уфа 2007, 2230.46kb.
- Учебно-методический комплекс по дисциплине «Управление рисками» Для специальности:, 1692.15kb.
- Учебно-методический комплекс по дисциплине «Экономика недвижимости» Астана 2010, 1852.8kb.
Лекция_6
Дисперсионный анализ для связанных выборок
Метод дисперсионного анализа для связанных выборок применяется в тех случаях, когда исследуется влияние разных градаций фактора или разных условий на одну и ту же выборку испытуемых. Градаций фактора должно быть не менее трех.
В данном случае различия между испытуемыми - возможный самостоятельный источник различий. Однофакторный дисперсионный анализ для связанных выборок позволит определить, что перевешивает - тенденция, выраженная кривой изменения фактора, или индивидуальные различия между испытуемыми. Фактор индивидуальных различий может оказаться более значимым, чем фактор изменения экспериментальных условий.
Пример 2. Группа из 5 испытуемых была обследована с помощью трех экспериментальных заданий, направленных на изучение интеллектуальной, настойчивости (Сидоренко Е. В., 1984). Каждому испытуемому индивидуально предъявлялись последовательно три одинаковые анаграммы: четырехбуквенная, пятибуквенная и шестибуквенная. Можно ли считать, что фактор длины анаграммы влияет на длительность попыток ее решения?
Таблица 2. Длительность решения анаграмм (сек)
| Код испытуемого | Условие 1. четырехбуквенная анаграмма | Условие 2. Пятибуквенная анаграмма | Условие 3. шестибуквенная анаграмма | Суммы по испытуемым |
| 1 | 5 | 235 | 7 | 247 |
| 2 | 7 | 604 | 20 | 631 |
| 3 | 2 | 93 | 5 | 100 |
| 4 | 2 | 171 | 8 | 181 |
| 5 | 35 | 141 | 7 | 183 |
| суммы | 51 | 1244 | 47 | 1342 |
Сформулируем гипотезы. Наборов гипотез в данном случае два.
Набор А.
Н0(А): Различия в длительности попыток решения анаграмм разной длины являются не более выраженными, чем различия, обусловленные случайными причинами.
Н1(А): Различия в длительности попыток решения анаграмм разной длины являются более выраженными, чем различия, обусловленные случайными причинами.
Набор Б.
Но(Б): Индивидуальные различия между испытуемыми являются не более выраженными, чем различия, обусловленные случайными причинами.
Н1(Б): Индивидуальные различия между испытуемыми являются более выраженными, чем различия, обусловленные случайными причинами.
Последовательность операций в однофакторном дисперсионном анализе для связанных выборок:
1. подсчитаем SSфакт - вариативность признака, обусловленную действием исследуемого фактора по формуле (1).
 ,
, где Тс – сумма индивидуальных значений по каждому из условий (столбцов). Для нашего примера 51, 1244, 47 (см. табл. 2); с – количество условий (градаций) фактора (=3); n – количество испытуемых в каждой группе (=5); N – общее количество индивидуальных значений (=15);
 - квадрат общей суммы индивидуальных значений (=13422)
- квадрат общей суммы индивидуальных значений (=13422) 2. подсчитаем SSисп - вариативность признака, обусловленную индивидуальными значения испытуемых.

где Ти – сумма индивидуальных значений по каждому испытуемому. Для нашего примера 247, 631, 100, 181, 183 (см. табл. 2); с – количество условий (градаций) фактора (=3); N – общее количество индивидуальных значений (=15);
3. подсчитаем SSобщ – общую вариативность признака по формуле (2):

4. подсчитаем случайную (остаточную) величину SSсл, обусловленную неучтенными факторами по формуле (3):

5. число степеней свободы равно (4):
 ;
;  ;
;  ;
; 
6. «средний квадрат» или математическое ожидание суммы квадратов, усредненная величина соответствующих сумм квадратов SS равна (5):
 ;
; 

7. значение статистики критерия Fэмп рассчитаем по формуле (6 ):
 ;
; 
8. определим Fкрит по статистическим таблицам Приложения 3 для df1=k1=2 и df2=k2=8 табличное значение статистики Fкрит_факт=4,46, и для df3=k3=4 и df2=k2=8 Fкрит_исп=3,84
9. Fэмп_факт > Fкрит_факт (6,872>4,46), следовательно принимается альтернативная гипотеза.
10. Fэмп_исп < Fкрит_исп (1,054<3,84), следовательно принимается нулевая гипотеза.
Вывод: различия в объеме воспроизведения слов в разных условиях являются более выраженными, чем различия, обусловленные случайными причинами (р<0,05). Индивидуальные различия между испытуемыми являются не более выраженными, чем различия, обусловленные случайными причинами.
Лекция_7
Двухфакторный анализ
- Связь задач двухфакторного и однофакторного анализа
Продолжая тему исследования зависимостей, начатую в главе 6, рассмотрим задачу о действии на измеряемую величину (отклик) двух факторов. В этой задаче мы предполагаем, что на отклик могут влиять два фактора, каждый из которых принимает конечное число значений (уровней), и интересуемся тем, как влияют эти факторы на изучаемый отклик и влияют ли вообще. Такие задачи характерны как для промышленных и технологических экспериментов, так и для гуманитарных исследований. Остановимся более подробно на одном из распространенных случаев возникновения задач двухфакторного анализа.
Бывает, что в рамках однофакторной модели (см. гл. 6) влияние интересующего нас фактора не проявляется, хотя содержательные соображения указывают, что такое влияние должно быть. Иногда это влияние проявляется, но точность выводов о количественной стороне этого влияния недостаточна. Причиной такого явления может быть большой внутригрупповой разброс, на фоне которого действие фактора остается незаметным или почти незаметным. Очень часто этот разброс вызывается не только случайными причинами, но также действием еще одного фактора. Если мы в состоянии указать такой фактор, можно попытаться включить его в модель, чтобы уменьшить статистическую неоднородность наблюдений и благодаря этому выявить действие на отклик закономерных причин. Конечно, не всегда удается поправить дело введением одного «мешающего» фактора и переходом к двухфакторным схемам, как выше. Иногда приходится рассматривать и трех-, и многофакторные модели. Замысел во всех этих случаях остается прежним.
К задачам двухфакторного или многофакторного анализа часто приводят также исследования по оптимизации технологических процессов. При этом чаще всего заранее известно, что оба фактора оказывают значимое влияние на отклик, а исследователя интересует численная оценка этого влияния с целью выбора оптимального уровня факторов.

 Иногда факторы разделяют на важные и мешающие, но это совсем не обязательно. В ряде задач факторы содержательно равноправны для экспериментатора. Эти нюансы мало влияют на статистические модели, они могут сказаться только на постановках статистических вопросов.
Иногда факторы разделяют на важные и мешающие, но это совсем не обязательно. В ряде задач факторы содержательно равноправны для экспериментатора. Эти нюансы мало влияют на статистические модели, они могут сказаться только на постановках статистических вопросов.Таблица двухфакторного анализа
Рассмотрим, как изменяется таблица однофакторного анализа, приведенная в пункте 6. при включении в модель действия мешающего фактора.
Назовем главный фактор фактором А, а мешающий фактор — фактором В. Пусть фактор А принимает k, а фактор В — п различных значений. Фактор В разбивает все объекты наблюдения на п блоков, каждый блок образуют наблюдения, проведенные при одном уровне фактора В. В блоке отклики могут значимо различаться только за счет-применения к ним различных обработок, то есть за счет различных уровней фактора А. Уровни фактора А (обработки) отображаются в таблице по столбцам, а уровни фактора В (блоки) — по строкам. Традиционная терминология «блок-обработка» в применении к
Таблица 7.1
| | Обработки | |||
| Блоки | 1 | 2 | | к |
| 1 2 п | in a?2i Хп1 | Ж12 Х22 Хп2 | | Xlk Х2к Хпк |
факторам В и А сложилась как результат различного отношения к этим факторам, один из которых является мешающим, а другой определяющим.
Таблица 7.1, содержащая п х к наблюдений (по одному наблюдению в клетке) является основной таблицей двухфакторного анализа. Ее отличие от таблицы однофакторного анализа заключается в том, что наблюдения в любом столбце не являются однородными, то есть могут не образовывать выборки (если влияние мешающего фактора значимо). Для описания такой двухфакторной таблицы требуются более сложные вероятностные модели, чем для однофакторного анализа.
Аддитивная модель данных двухфакторного эксперимента
при независимом действии факторов
Для описания данных таблицы 7.1 двухфакторного эксперимента в большинстве случаев оказывается приемлемой аддитивная модель. Она предполагает, что значение отклика хц является суммой самостоятельных вкладов соответствующих уровней каждого из факторов и независимых от этих факторов случайных величин. Последние отражают внутреннюю изменчивость отклика при фиксированных уровнях факторов, которая может порождаться различными причинами.
Таким образом, каждое наблюдение хц представляется в виде:
При этом числа b\,... ,bn являются результатом влияния на отклик мешающего фактора В, действие которого разбивает все данные на блоки. Поэтому величины Ьх,... , Ьп называют эффектами блоков. Числа t%,... , tk отражают действие на отклик интересующего нас фактора А и именуются эффектами обработки. Относительно случайных величин


 eij предполагается, что они одинаково распределены и независимы в совокупности. Различные методы двухфакторного анализа требуют от их распределения либо только непрерывности, либо принадлежности к нормальному семейству распределений N(0,a2) со средним 0 и некоторой неизвестной дисперсией а2. Оба эти случая разобраны ниже.
eij предполагается, что они одинаково распределены и независимы в совокупности. Различные методы двухфакторного анализа требуют от их распределения либо только непрерывности, либо принадлежности к нормальному семейству распределений N(0,a2) со средним 0 и некоторой неизвестной дисперсией а2. Оба эти случая разобраны ниже.Непараметрические критерии проверки гипотезы
об отсутствии эффектов обработки
Критерий Фридмана (произвольные альтернативы)
Непараметрический критерий Фридмана для проверки гипотезы Но против альтернативы о наличии влияния фактора А используется в случае, если о распределении случайных величин ец, г = 1,... , п, j = 1,... , fc в модели (7.2) известно только то, что оно непрерывно, а сами величины eij независимы в совокупности. (То, что е- одинаково распределены, было оговорено раньше.) Критерий основан на идее перехода от значений величин хц в таблице двухфакторного анализа к их рангам. В отличие от однофакторного анализа, ранжирование происходит не по всей совокупности величин хц, а поблочно, то есть рассматривается каждая отдельная строка таблицы 7.1 и при фиксированном индексе i осуществляется ранжирование величин Жу при j = 1,... , к. Тем самым устраняется влияние «мешающего» фактора В, значение которого для каждой строки таблицы постоянно.
Обозначим полученные ранги величин хц через гц. Ясно, что значения nj изменяются от 1 до fc, а соответствующая строка рангов представляет собой некоторую перестановку чисел 1,2,... , fc. Для простоты изложения будем предполагать, что среди элементов хц, стоящих в одной строке таблицы (7.1), нет совпадающих (в противном случае следует использовать средние ранги). При гипотезе Hq : т-\_ = т2 = • • • = Tk = О каждая строка рангов Гц, rj2,..., r,fc будет представлять случайную перестановку чисел от 1 до fc, причем все fc! перестановок равновероятны. Введем величину: r.j — (X=ir«j)' являющуюся средним значением рангов по столбцу j. При гипотезе Но в силу равновероятности всех перестановок рангов в каждой строке значение r.j для каждого j не должно сильно отличаться от величины г.. = (fc +1)/2, которая представляет собой общий средний ранг всех элементов таблицы рангов. (Действительно, сумма рангов по всей таблице есть nfc(fc -f l)/2. Средний ранг получается делением на число пк элементов таблицы).
Здесь множитель, стоящий перед знаком суммы, добавлен для того, чтобы S имело простое асимптотическое распределение. В вычислительном плане более удобна другая форма записи величины S, а именно:
(7.4)
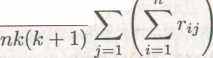
Как отмечалось выше, при справедливости гипотезы Но величины (r.j — г..)2 в выражении (7.3) с большой вероятностью сравнительно малы для всех j, и, следовательно, значение S сравнительно невелико.
 А при нарушении Яо суммы рангов в одних столбцах будут тяготеть к превышению значения среднего ранга г.., а в других — к уменьшению этого значения, в зависимости от знака величины т,- ф 0. Это приводит к возрастанию статистики Фридмана S. Из этих соображений вытекает вид критерия Фридмана для проверки гипотезы Яо : т\ = т2 = • • • = Tfc = 0 против альтернативы наличия эффектов обработки.
А при нарушении Яо суммы рангов в одних столбцах будут тяготеть к превышению значения среднего ранга г.., а в других — к уменьшению этого значения, в зависимости от знака величины т,- ф 0. Это приводит к возрастанию статистики Фридмана S. Из этих соображений вытекает вид критерия Фридмана для проверки гипотезы Яо : т\ = т2 = • • • = Tfc = 0 против альтернативы наличия эффектов обработки.Критерий Пейджа (альтернативы с упорядочением)
Назначение. Часто целью исследования является установление преимущества одного метода обработки над другим. Если таких обработок несколько, возможно предположение, что их эффективность возрастает в определенном направлении, например, по мере увеличения интенсивности воздействия. Для того, чтобы подтвердить или опровергнуть такое предположение, снова обратимся к проверке Яо. Но на этот раз постараемся выбрать критерий, чувствительный именно к альтернативам о возрастании (вариант: убывании) эффекта. Против такой специальной и более узкой группы альтернатив можно предложить ориентированный именно на эту ситуацию критерий Пейджа.
Критерий Пейджа предназначен для проверки гипотезы Яо об отсутствии эффектов обработки ( До : т% = т% = • •- = ть) против альтернатив с упорядочением: т\ Т2 • • • т, где хотя бы одно из неравенств строгое.
Статистика Пейджа. Введем величину г,- как rj = ХГ=1гу- (-'та' тистика Пейджа L по определению есть: Вид критерия. Критерий проверки гипотезы Яо против альтернатив с упорядочением на уровне значимости а имеет вид:
- принять Яо, если L < l(a,k,n);
- отклонить Яо в пользу альтернативы, если L > l(a,k,n),
где функция l(a,k,n) удовлетворяет уравнению P{L > l(a,k,n)} = a.
Таблицы и асимптотика. Для значений к = 3, те = 2(1)20 и к = 4(1)8, те = 2(1)12 таблица приближенных значений l(a,k,n) дана в [115]. В случае больших значений /сите для нахождения процентных точек следует использовать асимптотическое распределение статистики L. Рассмотрим величину L*:
(7.6)
При справедливости Яо статистика L* имеет при те —> оо асимптотическое распределение N(0,1) (сведения о более точной аппроксимации можно найти в [65]). Следовательно, приближенный критерий для проверки Яо против альтернатив с упорядочением на уровне значимости а имеет вид: принять Яо, если L* < za, в противном случае — отклонить Яо в пользу альтернативы. Здесь za — а-процентная точка стандартного нормального распределения.
Если в пределах строки исходной двухфакторной таблицы встречаются совпадающие значения, надо использовать средние ранги. Чем больше таких совпадений, тем более приближенными становятся выводы.
