Учебно-методический комплекс по дисциплине «Анализ данных и прогнозирование экономики» для студентов специальностей: «Экономика» Астана 2010

Вид материала

Учебно-методический комплекс

Содержание Задания для самостоятельной работы 2.3 Генерация случайных величин Генерация случайных чисел Задание для самостоятельной работы Лабораторная работа №3 СПА (К.Роджерс, Р.Даймонд) Лабораторная работа №4 Лабораторная работа №5 Таблицы значений функции f(x) и F(x) Выявление различий в уровне исследуемого признака. Q-критерий Розенбаума, U-критерий Манна-Уитни, H-критерий Крускала-Уолиса, S- Показатели сокращения психологической дистанции (в %) после социодраматической замены ролей в группе протагонистов (n1=8)ч суфле Показатели интенсивности внутреннего сопротивления при обращении в службу знакомств (в мм) Индивидуальное значение по фактору N 16PF в 4 возрастных группах руководителей (по данным Е. В. Сидоренко, 1987) Лабораторная работа №7

Подобный материал:

• Учебно-методический комплекс по дисциплине: «анализ проектов» для студентов специальностей, 2311.99kb.
• Учебно-методический комплекс для студентов по дисциплине «оценка бизнеса и инноваций», 4385.11kb.
• Учебно-методический комплекс дисциплины: Прогнозирование национальной экономики Специальность, 345.29kb.
• Учебно-методический комплекс по дисциплине «Экономика и управление в акционерных обществах», 610.54kb.
• Учебно-методический комплекс по дисциплине «Инвестиционная деятельность предприятия», 593.61kb.
• Учебно-методический комплекс по дисциплине «финансы» астана, 2010, 1311.57kb.
• Учебно-методический комплекс по дисциплине «Институциональная экономика» Для специальности:, 1370.37kb.
• Учебно-методический комплекс по дисциплине теневая экономика уфа 2007, 2230.46kb.
• Учебно-методический комплекс по дисциплине «Управление рисками» Для специальности:, 1692.15kb.
• Учебно-методический комплекс по дисциплине «Экономика недвижимости» Астана 2010, 1852.8kb.

Задания для самостоятельной работы

1. Построить график нормальной функции плотности распределения f(x) при x, меняющемся от 20 до 40 с шагом 1 при =3.

2.3 Генерация случайных величин

Еще одним аспектом использования законов распределения вероятностей являет­ся генерация случайных величин. Бывают ситуации, когда необходимо получить пос­ледовательность случайных чисел. Это, в частности, требуется для моделирования объектов, имеющих случайную природу, по известному распределению вероятно­стей.

Процедура генерации случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из одного или не­скольких распределений.

В MS Excel для генерации СВ используются функции из категории Математические:

СЛЧИС () – выводит на экран равномерно распределенные случайные числа больше или равные 0 и меньшие 1;

СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран случайное число, лежащее между про­извольными заданными значениями.

В случае использования процедуры Генерация случайных чисел из пакета Анализа необходимо запол­нить следующие поля:

- число переменных вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все столбцы в выходном диапазоне будут заполнены;

- число случайных чисел вводится число случайных значений, которое необ­ходимо вывести для каждой переменной, если число случайных чисел не будет введе­но, то все строки выходного диапазона будут заполнены;

- в поле распределение необходимо выбрать тип распределения, которое следует использовать для генерации случайных переменных:

1. равномерное - характеризуется верxней и нижней границами. Переменные из­влекаются с одной и той же вероятностью для всех значений интервала.

2. нормальное — характеризуется средним значением и стандартным отклонени­ем. Обычно для этого распределения используют среднее значе­ние 0 и стандартное отклонение 1.

3. биномиальное — характеризуется вероятностью успеха (величина р) для неко­торого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной переменной;

4. дискретное — характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого, содержаще­го значения, и правого, содержащего вероятности, связанные со значением в дан­ной строке. Сумма вероятностей должна быть равна 1;

5. распределения Бернулли, Пуассона и Модельное.

- в поле случайное рассеивание вводится произвольное значение, для которого необ­ходимо генерировать случайные числа. Впоследствии можно снова использовать это значение для получения тех же самых случайных чисел.

- выходной диапазон вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на эк­ран будет выведено сообщение в случае возможного наложения выходного диапа­зона на исходные данные.

Рассмотрим пример.

Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы первые блюда чередовались в случайном порядке.

Решение

1. Пронумеруем первые блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
   
2. Укажем желаемую вероятность появления каждого первого блюда. Пусть все блюда будут равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
   
3. В меню Сервис выбираем пункт Анализ данных и далее указываем строку Генерация случайных чисел. В появившемся диалоговом окне указываем Число переменных — 1, Число случайных чисел — 30 (количество дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной интервал значений и вероятностей вводим (мышью) диапазон, содержащий номера супов и их вероятности. – А2:В5.
   
4. Указываем выходной диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3, 4.
   

Задание для самостоятельной работы

1. Сформировать выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
   
2. Сформировать выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
   
3. Пусть спортсмену необходимо составить график тренировок на 10 дней, так чтобы дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
   
4. Составить расписание внеклассных мероприятий на неделю для случайного проведения: семинаров, интеллектуальных игр, КВН и спец. курса.
   
5. Составить расписание на месяц для случайной демонстрации на телевидении одного из четырех рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1 должна быть в два раза выше, чем остальных рекламных роликов.
   

Лабораторная работа №3

Применение инструментальных средств для решения основных задач математической статистики (вариант будет разобран на лабораторной)

1) по результатам методики СПА (К.Роджерс, Р.Даймонд), проанализируйте особенности социально-психологической адаптации студентов 1-го курса обучения; 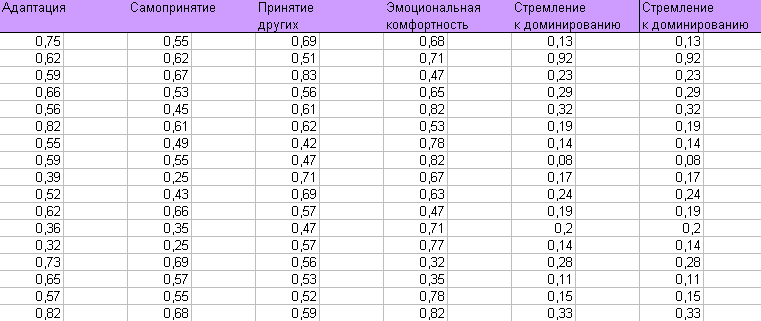2) постройте гистограмму распределения для параметра "Адаптация" и, исходя из полученных данных, дайте характеристику выборке по данному параметру.

Лабораторная работа №4

Алгоритмы параметрических критериев. Критерий Стьюдента. Критерий Фишера. В решении задач обязательно должны быть: 1)Условие задачи. 2)Формулировка гипотез. 3)Решение задачи. 4)Вывод.

Задача №1 Детям давались обычные арифметические задания, после чего одной случайно выбранной половине учащихся сообщали, что они не выдержали испытания, а остальным обратное. Затем, у каждого ребенка спрашивали, сколько секунд ему бы потребовалось для решения аналогичной задачи. Экспериментатор вычислял разность между называемым ребенком в временем (x1) и результатом выполненного задания (x2). Ожидалось, что сообщение о неудаче вызовет некоторую неадекватность самооценки ребенка. Проверяемая гипотеза (на уровне a=0.05) состояла в том, что дисперсия совокупности самооценок не зависит от сообщений об удаче или неудаче.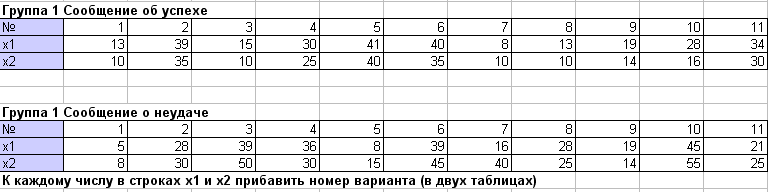

Задача №2 Исследовалось влияние условий воспитания в детском доме детей на интеллектуальное развитие детей. При использовании стандартного теста интеллекта были получены следующие данные (N=36) 91, 96, 99, 108, 108, 122, 101, 96, 125, 82, 116, 102, 92, 112, 84, 102, 121, 109, 107, 115, 93, 113, 113, 103, 82, 120, 90, 107, 102, 104, 110, 121, 112, 97, 121,89. (Для каждого числа прибавить номер варианта V). Исследователя интересовало, превышает ли интеллект воспитанников детского дома нормативный показатель А=100+V-2. Для принятия статистического решения уровень a=0.05.

Задача №3 Имеются 2 выборки по объектам исследования 1)104; 103,5; 104; 102; 104; 103,5; 103,5; 104; 103. 2)104; 102; 103; 103; 103; 102; 102; 102; 103 ; 102; 101,5; 102;101. (Для каждого числа прибавить номер варианта V). Предположив, что соответствующие генеральные совокупности имеют нормальное распределение, необходимо установить наличие различий в уровнях средних значений исследуемого признака при уровне значимости а=0,05.

Задача №4 На группе из 8 рабочих изучалось время выполнения одних и тех же технологических операций (в мин.): X- время выполнения операции в 1-ый раз. Y- время выполнения операции после 3-х повторов. Установить, зависит ли время выполнения операций от количества их повторений. Исходные данные: 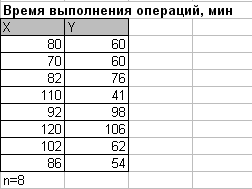(Для каждого числа прибавить номер варианта V).

Задача №5 В 2-х группах по 11 объектов исследования в каждой, изучались различия по некоторому признаку. Измеренные значения признака в первой и второй группах в таблице: 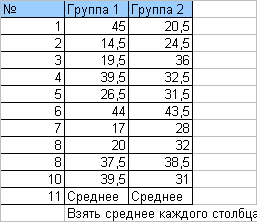Необходимо проверить наличие различий по выборкам используя критерий Фишера. (Для каждого числа прибавить номер варианта V).

Лабораторная работа №5

Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона (Пример решения задачи)

1)Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном рампределении генеральной совокупности Х с эампирическим распределением выборки: V - номер варианта. 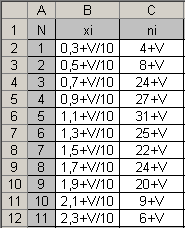2)Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном рампределении генеральной совокупности Х с эампирическим распределением выборки: 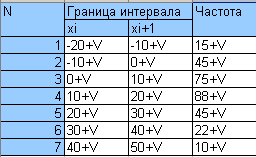V - номер варианта. Таблицы значений функции f(x) и F(x)

Вычисления можно проводить в Excel.

 

Лабораторная работа №6

Выявление различий в уровне исследуемого признака. Q-критерий Розенбаума, U-критерий Манна-Уитни, H-критерий Крускала-Уолиса, S-критерий тенденций Джонкира. (К каждому числу прибавлять номер варианта)

Задача 1.

В группе слушателей ФПК по педагогике и психологии назрел глухой конфликт между иногородними слушателями и слушателями, проживавшими в Санкт-Петербурге, где и происходили занятия. В курсе психологического практикума по групповой психологии иногородним слушателям было предложено принять на себя роль петербуржцев и участвовать в споре на их стороне. 8 слушателей были протагонистами -активными игроками, перевоплотившимися в петербуржцев, а 8 других суфлировали им, подсказывая реплики и ссылки на те или иные факты. После этого сеанса социодраматической замены ролей участникам был задан вопрос: "Если принять за 100% психологическую дистанцию между Вами и петербуржцами до дискуссии, то на сколько процентов она сократилась или увеличилась после дискуссии?" Результаты представлены в таблице. Все показатели имеют отрицательный знак, что свидетельствует о сокращении дистанции (Сидоренко Е. В., 1992). Могут ли эти данные использоваться как подтверждение идеи Д. Л. Морено о том, что принятие на себя роли оппонента способствует сближению с ним (Moreno G. L., 1934)? Показатели сокращения психологической дистанции (в %) после социодраматической замены ролей в группе протагонистов (n1=8)ч суфлеров (n2=8) V-номер варианта (V<15) Значения 8-ой строки округлить.

Задача 2.

В исследовании С.К. Скаковского (1990) изучалась проблема психологических барьеров при обращении в службу знакомств у мужчин и женщин. В эксперименте участвовали 19 мужчин и 25 женщины в возрасте от 17 до 45 лет (средний возраст 32,5 года). Испытуемые Должны были отметить на отрезке точку, соответствующую интенсивности внутреннего сопротивления, которое им пришлось преодолеть, чтобы обратиться в службу знакомств. Длина отрезка, отражающая максимально возможное сопротивление, составляла 100 мм. В Табл. приведены показатели интенсивности сопротивления, выраженные в миллиметрах. Можно ли утверждать, что мужчинам приходится преодолевать субъективно более мощное сопротивление? Показатели интенсивности внутреннего сопротивления при обращении в службу знакомств (в мм) 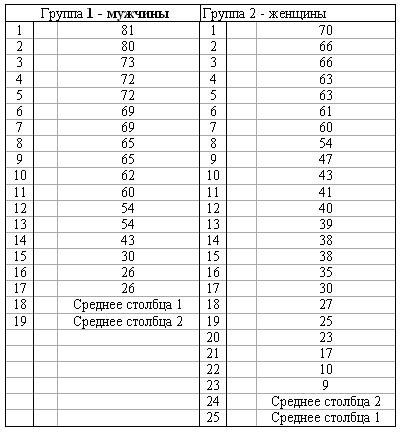К каждому числу прибавить номер варианта (V<15) Значения средних округлить.

Задача 3. (Джонкира, Крускала-Уоллиса)

В выборке из 32 мужчин-руководителей подразделений крупного промышленного предприятия Санкт-Петербурга перед началом курса тренинга партнерского общения проводилось обследование с помощью 16-факторного личностного опросника Р. Б. Кеттелла (форма А). В Табл. приведены индивидуальные значения испытуемых по фактору N, отражающему житейскую искушенность и проницательность. Данные представлены в "сырых" баллах и сгруппированы по четырем возрастным группам. Можно ли утверждать, что есть определенная тенденция изменения значений фактора N при переходе от группы к группе? Индивидуальное значение по фактору N 16PF в 4 возрастных группах руководителей (по данным Е. В. Сидоренко, 1987) 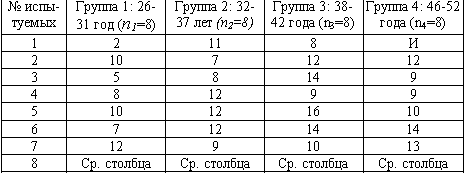К каждому числу прибавить номер варианта (V<15) Значения средних округлить.

Лабораторная работа №7

Оценка достоверности сдвига в значениях исследуемого признака.G-критерий знаков. G-критерий Вилкоксона.Критерий Фридмана. L-критерий тенденций Пейджа. (К каждому числу прибавлять номер варианта)

Задача 1.

Психолог провидит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить будет ли уменьшаться количество ошибок внимания у младших школьников после спец. коррекционных упражнений? (Критерий Вилкоксона) V-номер варианта ) Значения 20-ой и 21-ой строки округлить.

Задача 2.

Шести школьникам предъявляют тест Равена. Фиксируется время решения каждого задания. Выясняется вопрос - будут ли найдены статистически значимые различия между временем решения первых трех заданий теста. ( Критерий Фридмана) К каждому числу прибавить номер варианта Значения средних округлить.

Задача 3.

Продолжая исследования, психолог решил проверить гипотезу. Действительно ли время решения задания увеличивается (от первой задачи к третьей) (Критерий Пейджа) Данные взять из второй задачи

Задача 4.

Психолог проводит групповой тренинг. Его задача - выяснить, будет ли эффективен данный конкретный вариант тренинга для снижения уровня тревожности участников? (Критерий знаков) V-номер варианта )

Задача 5.

Получив отрицательные результаты, психолог внес в способ тренинга соответствующие коррективы. И опять выдвинул гипотезу: улучшенный вариант тренинга позволяет эффективно снижать уровень тревожности испытуемых. (Критерий знаков) (V-номер варианта ) Средние - округлить.