Учебно-методический комплекс по дисциплине «Анализ данных и прогнозирование экономики» для студентов специальностей: «Экономика» Астана 2010
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс по дисциплине: «анализ проектов» для студентов специальностей, 2311.99kb.
- Учебно-методический комплекс для студентов по дисциплине «оценка бизнеса и инноваций», 4385.11kb.
- Учебно-методический комплекс дисциплины: Прогнозирование национальной экономики Специальность, 345.29kb.
- Учебно-методический комплекс по дисциплине «Экономика и управление в акционерных обществах», 610.54kb.
- Учебно-методический комплекс по дисциплине «Инвестиционная деятельность предприятия», 593.61kb.
- Учебно-методический комплекс по дисциплине «финансы» астана, 2010, 1311.57kb.
- Учебно-методический комплекс по дисциплине «Институциональная экономика» Для специальности:, 1370.37kb.
- Учебно-методический комплекс по дисциплине теневая экономика уфа 2007, 2230.46kb.
- Учебно-методический комплекс по дисциплине «Управление рисками» Для специальности:, 1692.15kb.
- Учебно-методический комплекс по дисциплине «Экономика недвижимости» Астана 2010, 1852.8kb.
7.2.2 Коэффициент корреляции Пирсона
Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 г. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон.
Коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y. Формула расчета коэффициента корреляции построена таким образом, что, если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. Если же связь между переменными X и Y не линейна, то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное отношение.
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 — являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно произошла ошибка в вычислениях.
Знак коэффициента корреляции очень важен для интерпретации полученной связи. Подчеркнем еще раз, что если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости.
В общем виде формула для подсчета коэффициента корреляции такова:
 (7)
(7) где хi — значения, принимаемые в выборке X,
yi — значения, принимаемые в выборке Y;
 — средняя по X,
— средняя по X,  — средняя по Y.
— средняя по Y. Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и У распределены нормально.
В формуле (7) встречается величина
 при делении на n (число значений переменной X или Y) она называется ковариацией. Формула (7) предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y.
при делении на n (число значений переменной X или Y) она называется ковариацией. Формула (7) предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y. Число степеней свободы k=n-2.
Пример 3. 10 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Исследователя интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X — обозначает среднее время решения наглядно-образных, а переменная Y— среднее время решения вербальных заданий тестов [2].
Решение. Представим исходные данные в виде таблицы 4, в которой введены дополнительные столбцы, необходимые для расчета по формуле (7).
Таблица 4
| № испытуемых | x | y | хi-  | (хi-  )2 )2 | yi-  | (yi-  )2 )2 |  |
| 1 | 19 | 17 | -16,7 | 278,89 | -7,2 | 51,84 | 120,24 |
| 2 | 32 | 7 | -3,7 | 13,69 | -17,2 | 295,84 | 63,64 |
| 3 | 33 | 17 | -2,7 | 7,29 | -7,2 | 51,84 | 19,44 |
| 4 | 44 | 28 | 8,3 | 68,89 | 3,8 | 14,44 | 31,54 |
| 5 | 28 | 27 | -7,7 | 59,29 | 2,8 | 7,84 | -21,56 |
| 6 | 35 | 31 | -0,7 | 0,49 | 6,8 | 46,24 | -4,76 |
| 7 | 39 | 20 | 3,3 | 10,89 | -4,2 | 17,64 | -13,86 |
| 8 | 39 | 17 | 3,3 | 10,89 | -7,2 | 51,84 | -23,76 |
| 9 | 44 | 35 | 8,3 | 68,89 | 10,8 | 116,64 | 89,64 |
| 10 | 44 | 43 | 8,3 | 68,89 | 18,8 | 353,44 | 156,04 |
| Сумма | 357 | 242 | | 588,1 | | 1007,6 | 416,6 |
| Среднее | 35,7 | 24,2 | | | | | |
Рассчитываем эмпирическую величину коэффициента корреляции по формуле (7):

Определяем критические значения для полученного коэффициента корреляции по таблице Приложения 3. При нахождении критических значений для вычисленного коэффициента линейной корреляции Пирсона число степеней свободы рассчитывается как k = n – 2 = 8.
ккрит=0,72 > 0,54 , следовательно, гипотеза Н1 отвергается и принимается гипотеза H0, иными словами, связь между временем решения наглядно-образных и вербальных заданий теста не доказана.
Лекция_11
Параметрические критерии
В группу параметрических критериев методов математической статистики входят методы для вычисления описательных статистик, построения графиков на нормальность распределения, проверка гипотез о принадлежности двух выборок одной совокупности. Эти методы основываются на предположении о том, что распределение выборок подчиняется нормальному (гауссовому) закону распределения. Среди параметрических критериев статистики нами будут рассмотрены критерий Стьюдента и Фишера.
6.1.1 Методы проверки выборки на нормальность
Чтобы определить, имеем ли мы дело с нормальным распределением, можно применять следующие методы:
1) в пределах осей можно нарисовать полигон частоты (эмпирическую функцию распределения) и кривую нормального распределения на основе данных исследования. Исследуя формы кривой нормального распределения и графика эмпирической функции распределения, можно выяснить те параметры, которыми последняя кривая отличается от первой;
2) вычисляется среднее, медиана и мода и на основе этого определяется отклонение от нормального распределения. Если мода, медиана и среднее арифметическое друг от друга значительно не отличаются, мы имеем дело с нормальным распределением. Если медиана значительно отличается от среднего, то мы имеем дело с асимметричной выборкой.
3) эксцесс кривой распределения должен быть равен 0. Кривые с положительным эксцессом значительно вертикальнее кривой нормального распределения. Кривые с отрицательным эксцессом являются более покатистыми по сравнению с кривой нормального распределения;
4) после определения среднего значения распределения частоты и стандартного oтклонения находят следующие четыре интервала распределения сравнивают их с действительными данными ряда:
а)
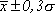 — к интервалу должно относиться около 25% частоты совокупности,
— к интервалу должно относиться около 25% частоты совокупности, б)
 — к интервалу должно относиться около 50% частоты совокупности,
— к интервалу должно относиться около 50% частоты совокупности, в)
 — к интервалу должно относиться около 75% частоты совокупности,
— к интервалу должно относиться около 75% частоты совокупности, г)
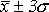 — к интервалу должно относиться около 100% частоты совокупнос
— к интервалу должно относиться около 100% частоты совокупносНепараметрические критерии
Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.
.2.2 Критерий χ2 (хи-квадрат)
Критерий χ2 (хи-квадрат) применяется для сравнения распределений объектов двух совокупностей на основе измерений по шкале наименований в двух независимых выборках.
Предположим, что состояние изучаемого свойства (например, выполнение определенного задания) измеряется у каждого объекта по шкале наименований, имеющей только две взаимоисключающие категории (например: выполнено верно — выполнено неверно). По результатам измерения состояния изучаемого свойства у объектов двух выборок составляется четырехклеточная таблица 2X2. (см. табл. 6).
Таблица 6.
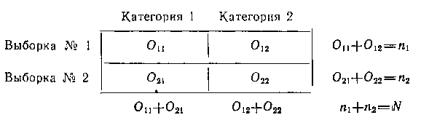
В этой таблице Оij — число объектов в i-ой выборке, попавших в j-ую категорию по состоянию изучаемого свойства; i=1,2 – число выборок; j=1,2 – число категорий;; N — общее число наблюдений, равное О11 + О12 + О21 + О22 или n1+n2.
Тогда на основе данных таблицы 2X2 (см. табл. 6) можно проверить нулевую гипотезу о равенстве вероятностей попадания объектов первой и второй совокупностей в первою (вторую) категорию шкалы измерения проверяемого свойства, например гипотезу о равенстве вероятностей верного выполнения некоторого задания учащимися контрольных и экспериментальных классов.
При проверке нулевых гипотез не обязательно, чтобы значения вероятностей р1 и р2 были известны, так как гипотезы только устанавливают между ними некоторые соотношения (равенство, больше или меньше).
Для проверки рассмотренных выше нулевых гипотез по данным таблицы 2X2 (см. табл. 6) подсчитывается значение статистики критерия Т по следующей общей формуле:
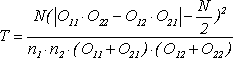 (9)
(9)где n1, n2 — объемы выборок, N = n1 + n2 — общее число наблюдений.
Проводится проверка гипотезы H0: p1£p2 — при альтернативе Н1: р1>р2. Пусть a — принятый уровень значимости. Тогда значение статистики Т, полученное на основе экспериментальных данных, сравнивается с критическим значением статистики х1-2a,, которое определяется по таблице c2 c одной степенью свободы (см. Приложение 2) с учетом выбранного значения a. Если верно неравенство T
В связи с тем что замена точного распределения статистики Т распределением c2 c одной степенью свободы дает достаточно хорошее приближение только для больших выборок, применение критерия ограничено некоторыми условиями.
Критерий не рекомендуется использовать, если:
1) сумма объемов двух выборок меньше 20;
2) хотя бы одна из абсолютных частот в таблице 2X2, составленной на основе экспериментальных данных, меньше 5.
Пример 6. Проводился эксперимент, направленный на выявление лучшего из учебников, написанных двумя авторскими коллективами в соответствии с целями обучения геометрии и содержанием программы IX класса. Для проведения эксперимента методом случайного отбора были выбраны два района, большинство школ которых относились по расположению к сельским. Учащиеся первого района (20 классов) обучались по учебнику № 1, учащиеся второго района (15 классов) обучались по учебнику №2.
Рассмотрим методику сравнения ответов учителей экспериментальных школ двух районов па один из вопросов анкеты: «Доступен ли учебник в целом для самостоятельного чтения и помогает ли он усвоить материал, который учитель не объяснял в классе (Ответ: да — нет.)
Отношение учителей к изучаемому свойству учебников измерено по шкале наименований, имеющей две категории: да, нет. Обе выборки учителей случайные и независимые.
Ответы 20 учителей первого района и 15 учителей второго района распределим на две категории и запишем в форме таблицы 2Х2 (табл. 5).
Таблица 7.

Все значения в табл. 7 не меньше 5, поэтому в соответствии с условиями использования критерия c2 подсчет статистики критерия производится по формуле (9).
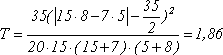
По таблице из приложения 2 для одной степени свободы (v=l) и уровня значимости a=0,05 найдем х1-aа =Ткритич = 3,84. Отсюда верно неравенство Тнаблюд<Ткритич (1,86<3,84). Согласно правилу принятия решений для критерия c2, полученный результат не дает достаточных оснований для отклонения нулевой гипотезы, т. е. результаты проведенного опроса учителей двух экспериментальных районов не дают достаточных оснований для отклонения предположения об одинаковой доступности учебников №1 и 2 для самостоятельного чтения учащимися.
Применение критерия хи-квадрат возможно и в том случае, когда объекты двух выборок из двух совокупностей по состоянию изучаемого свойства распределяются более чем на две категории. Например, учащиеся экспериментальных и контрольных классов распределяются на четыре категории в соответствии с отметками (в баллах: 2, 3, 4, 5), полученными учащимися за выполнение некоторой контрольной работы.
Результаты измерения состояния изучаемого свойства у объектов каждой выборки распределяются на С категорий. На основе этих данных составляется таблица 2ХС, в которой два ряда (по числу рассматриваемых совокупностей) и С колонок (по числу различных категорий состояния изучаемого свойства, принятых в исследовании).
Таблица 8.
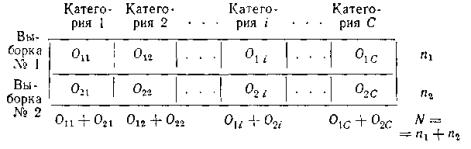
На основе данных таблицы 8 можно проверить нулевую гипотезу о равенстве вероятностей попадания объектов первой и второй совокупностей в каждую из i (i=l, 2, ..., С) категорий, т. е. проверить выполнение всех следующих равенств: р11= р21, p12 = p22, …, p1c = p2c. Возможна, например, проверка гипотезы о равенстве вероятностей получения отметок «5», «4», «3» и «2» за выполнение учащимися контрольных и экспериментальных классов некоторого задания.
Для проверки нулевой гипотезы с помощью критерия c2 на основе данных таблицы 2ХС подсчитывается значение статистики критерия Т по следующей формуле:
 (10)
(10)где п1 и п2 — объемы выборок.
Значение Т, полученное на основе экспериментальных данных, сравнивается с критическим значением х1-a, которое определяется по таблице c2 с k=С—1 степенью свободы с учетом выбранного уровня значимости a. При выполнении неравенства Т> х1-aа нулевая гипотеза отклоняется на уровне а и принимается альтернативная гипотеза. Это означает, что распределение объектов на С категорий по состоянию изучаемого свойства различно в двух рассматриваемых совокупностях.
Пример 7. Рассмотрим методику сравнения результатов письменной работы, проверявшей усвоение одного из разделов курса учащимися первого и второго районов.
Методом случайного отбора из учащихся первого района, писавших работу, была составлена выборка объемом 50 человек, из учащихся второго района — выборка объемом 50 человек. В соответствии со специально разработанными критериями оценки выполнения работы каждый ученик мог попасть в одну из четырех категорий: плохо, посредственно, хорошо, отлично. Результаты выполнения работы двумя выборками учащихся используем для проверки гипотезы о том, что учебник № 1 способствует лучшему усвоению проверяемого раздела курса, т. е. учащиеся первого экспериментального района в средне будут получать более высокие оценки, чем учащиеся второго района.
Результаты выполнения работы учащимися обеих выборок запишем в виде таблицы 2X4 (табл. 9).
Таблица 9.

В соответствии с условиями использования критерия c2 подсчет статистики критерия производится по корректированной формуле (10).
 =
=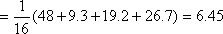
В соответствии с условиями применения двустороннего критерия хи-квадрат по таблице из приложения 2 для одной степени свободы (k=4-l=3) и уровня значимости a=0,05 найдем х1-aа =Ткритич = 7,815. Отсюда верно неравенство Тнаблюд<Ткритич (6,45<7,815). Согласно правилу принятия решений для критерия c2, полученный результат не дает достаточных оснований для отклонения нулевой гипотезы.
Лекция_12
Временные ряды: практический анализ
Порядок анализа временных рядов
Кратко опишем общий порядок прикладного статистического анализа временных рядов. Обычно целью такого анализа является построение математической модели ряда, с помощью которой можно объяснить поведение ряда и осуществить прогноз его дальнейшего поведения.
Построение и изучение графика. Анализ временного ряда обычно начинается с построения и изучения его графика. Если нестационарность временного ряда очевидна, то первым делом надо выделить и удалить нестационарную составляющую ряда. Методы, используемые для этого, описаны в п. 12.3. Процесс удаления тренда и других компонент ряда, приводящих к нарушению стационарности, может проходить в несколько этапов. На каждом из них рассматривается ряд остатков, полученный в результате вычитания из исходного ряда подобранной модели тренда, или результат разностных и других преобразований ряда. Кроме графиков, признаками нестационарности временного ряда могут служить не стремящаяся к нулю автокорреляционная функция (за исключением очень больших значений лагов) и наличие ярко выраженных пиков на низких частотах в периодограмме.
Подбор модели для временного ряда. После того, как исходный процесс максимально приближен к стационарному, можно приступить к подбору различных моделей полученного процесса. Цель этого этапа — описание и учет в дальнейшем анализе корреляционной структуры рассматриваемого процесса. При этом на практике чаще
-
 оценка дисперсии остатков, которая в дальнейшем может быть
оценка дисперсии остатков, которая в дальнейшем может быть
использована для построения доверительных интервалов про
гноза;
- анализ остатков с целью проверки адекватности модели.
Прогнозирование или интерполяция. Последним этапом анализа временного ряда может быть прогнозирование его будущих (экстраполяция) или восстановление пропущенных (интерполяция) значений и указания точности этого прогноза на базе подобранной модели. Обратим внимание, что хорошо подобрать математическую модель удается не для всякого временного ряда. Нередко бывает и так, что для описания подходят сразу несколько моделей. Неоднозначность подбора модели может наблюдаться как на этапе выделения детерминированной компоненты ряда, так и при выборе структуры ряда остатков. Поэтому исследователи довольно часто прибегают к методу нескольких прогнозов, сделанных с помощью разных моделей.
Методы анализа. Перечислим основные группы статистических приемов, используемых для анализа временных рядов:
- графические методы представления временных рядов и их со
путствующих числовых характеристик;
- методы сведения к стационарным процессам;
- методы исследования внутренних связей между элементами вре
менных рядов.
Ниже будет подробно рассказано о каждой из этих групп методов.
Графические методы анализа временных рядов
Зачем нужны графические методы. В выборочных исследованиях простейшие числовые характеристики описательной статистики (среднее, медиана, дисперсия, стандартное отклонение, коэффициенты асимметрии и эксцесса) обычно дают достаточно информативное представление о выборке. Графические методы представления и анализа выборок при этом играют лишь вспомогательную роль, позволяя лучше понять локализацию и концентрацию данных, их закон распределения.
Роль графических методов при анализе временных рядов совершенно иная. Дело в том, что табличное представление временного ряда и описательные статистики чаще всего не позволяют понять характер процесса, в то время как по графику временного ряда можно сделать довольно много выводов. В дальнейшем они могут быть проверены и уточнены с помощью расчетов.
Человеческий глаз довольно уверенно определяет по графику временного ряда:
- наличие тренда и его характер;
- наличие сезонных и циклических компонент;
- степень плавности или прерывистости изменений последова
тельных значений ряда после устранения тренда. По этому
показателю можно судить о характере и величине корреляции
между соседними элементами ряда.
Так графический анализ ряда обычно задает направление его дальнейшего анализа.
Построение и изучение графика. Построение графика временного ряда — совсем не такая простая задача, как это кажется на первый взгляд. Современный уровень анализа временных рядов предполагает использование той или иной компьютерной программы для построения их графиков и всего последующего анализа. Ряд полезных рекомендаций при построении графика вручную даны в [98]. Большинство статистических пакетов и электронных таблиц снабжено теми или иными методами настройки на оптимальное представление временного ряда, но даже при их использовании могут возникать различные проблемы, например:
- из-за ограниченности разрешающей способности экранов ком
пьютеров размеры выводимых графиков могут быть также огра
ничены;
- при больших объемах анализируемых рядов точки на экране,
изображающие наблюдения временного ряда, могут превратить
ся в сплошную черную полосу.
Для борьбы с этими затруднениями используются различные способы. Наличие в графической процедуре режима «лупы» или «увеличения» позволяет изобразить более крупно выбранную часть ряда, однако при этом становится трудно судить о характере поведения ряда на всем анализируемом интервале. Приходится распечатывать графики для отдельных частей ряда и состыковывать их вместе, чтобы увидеть картину поведения ряда в целом. Иногда для улучшения воспроизведения длинных рядов используется прореживание, то есть выбор и отображение на графике каждой второй, пятой, десятой и т.д. точки временного ряда. Эта процедура позволяет сохранить целостное представление ряда и полезна для обнаружения трендов. На практике полезно сочетание

 обеих процедур: разбиения ряда на части и прореживания, так как они позволяют подметить разные черты в поведении временного ряда.
обеих процедур: разбиения ряда на части и прореживания, так как они позволяют подметить разные черты в поведении временного ряда.Еще одну проблему при воспроизведении графиков создают выбросы — наблюдения, в несколько раз превышающие по величине большинство остальных значений ряда. Их присутствие тоже приводит к неразличимости колебаний временного ряда, так как масштаб изображения программа автоматически подбирает так, чтобы все наблюдения поместились на экране. Выбор другого масштаба на оси ординат устраняет эту проблему, но резко отличающиеся наблюдения при этом остаются за границами экрана.
Методы сведения к стационарности
После изучения графика временного ряда обычно пробуют выделить во временном ряде тренд, сезонные и периодические компоненты. После их исключения временной ряд должен стать стационарным. Кроме того, для облегчения дальнейшего анализа иногда используются преобразования значений временного ряда (точнее, той шкалы, в которой они измерены) — это позволяет приблизить распределение значений временного ряда к нормальному или сделать дисперсию этих значений более постоянной (иначе говоря, стабилизировать дисперсию).
Выделение тренда
Метод наименьших квадратов. Для оценки и удаления трендов из временных рядов чаще всего используется метод наименьших квадратов. Этот метод подробно обсуждался в гл. 8 при рассмотрении задач линейного регрессионного анализа.
Говоря языком регрессионного анализа, значения временного ряда xt рассматривают как отклик (зависимую переменную), а время t — как фактор, влияющий на отклик (независимую переменную):
где / — функция тренда (она обычно предполагается гладкой), в — неизвестные нам параметры (параметры модели временного ряда), a Si —
преобразование Бокса-Кокса, ко всем членам ряда прибавляют постоянную с. Члены преобразованного ряда получают по формуле
если выбранное Л > 0. Для Л = 0 преобразование Бокса-Кокса действует как уже упомянутое логарифмическое: yt — log(a;t + с).
Методы исследования структуры стационарного временного ряда
Цели и методы анализа
Цели анализа. В предыдущих параграфах этой главы мы рассматривали методы выделения из временного ряда детерминированной компоненты — тренда, сезонной и циклической компонент. После удаления детерминированной компоненты временной ряд должен свестись к стационарному процессу. Так что следующим шагом после выделения детерминированной компоненты должен быть анализ остатков, то есть изучение ряда, полученного из исходного временного ряда после исключения детерминированной компоненты. При этом могут ставиться следующие цели.
- Описание ряда с помощью той или иной модели, которая отражает зависимость между его соседними элементами. На базе построенной модели можно осуществлять прогноз будущего поведения ряда.
- Уточнение оценки дисперсии временного ряда. Эта оценка важна для прогнозирования, так как исходя из нее вычисляется ширина доверительной трубки прогноза. Привычные оценки дисперсии, которые мы использовали в регрессионном анализе.
- Проверка стационарности остатков (при нестационарности подбор детерминированной компоненты нуждается в уточнении).
Методы анализа. В качестве модели стационарных временных рядов чаще всего используются процессы авторегрессии, скользящего среднего и их комбинации. Этим моделям посвящена глава.
А для проверки стационарности ряда остатков и оценки его дисперсии на практике чаще всего используются выборочная автокорреляционная (коррелограмма, см. п. 11.10) и частная автокорреляционная функция. В пп. 12.4.2 и 12.4.3 мы рассмотрим методы интерпретации графиков этих функций.
Интерпретация графика коррелограммы
Анализ коррелограммы — это порой довольно непростая задача. О причинах возникающих при этом трудностей мы уже говорили. Здесь мы кратко остановимся на типичном поведении коррелограммы для некоторых классов временных рядов.
Для начала рассмотрим поведение коррелограммы для некоторых нестационарных рядов. В этом случае следует помнить, что коррелограмма практически не несет никакой информации о статистической зависимости или независимости членов временного ряда, однако она может отражать причины нарушения стационарности. Именно с этой точки зрения мы и рассматриваем два следующих примера.
Наличие тренда. Для временного ряда, содержащего тренд, коррелограмма не стремится к нулю с ростом значения лага к. Ее характерное поведение изображено на рис. 12.14, где коррелограмма построена для ряда урожайности зерновых (рис. 11.1а).
Наличие сезонных колебаний. Для ряда с сезонными колебаниями коррелограмма также будет содержать периодические всплески, соответствующие периоду сезонных колебаний. Это позволяет устанавливать предполагаемый период сезонности. Однако, как было сказано в п. 11.10, отдельные редкие выхода графика коррелограммы за границы доверительной трубки могут наблюдаться и у белого шума. Типичное поведение коррелограммы для ряда с сезонными колебаниями приведено на рис. 12.15, где она построена для данных месячных продаж шампанского в логарифмической шкале (рис. 12.12) после удаления из них линейного тренда.
Лекция_13
Анализ временных рядов на компьютере
Анализ временных рядов в SPSS
Методы анализа временных рядов широко представлены во многих универсальных статистических пакетах, включая разобранные в предыдущих главах STADIA и SPSS. Но анализ временных рядов — это очень специфическая область статистики, отличающаяся по кругу задач и методов их решения, а также по кругу пользователей, применяющих эти методы. Поэтому для анализа временных рядов имеются также и специализированные статистические пакеты. В этой главе мы рассмотрим способы решения рассмотренных выше задач в универсальном статистическом пакете SPSS и в специализированном статистическом пакете ЭВРИСТА. Выбор данных пакетов обусловлен следующими причинами.
Универсальный пакет SPSS занимает одно из первых мест в мире среди программ статистической обработки данных (см. приложения 1 и 2). Отечественным специалистам ранние версии SPSS в основном были известны как мощный инструмент обработки социологических и психологических данных. В связи с этим мы решили показать этот пакет с менее известной его стороны. Для нас также было важно познакомить пользователя с англоязычной терминологией в области анализа временных рядов.
Пакет ЭВРИСТА является одним из лучших специализированных отечественных пакетов для анализа временных рядов. Его функциональные возможности значительно шире стандартных процедур анализа временных рядов универсальных статистических пакетов. Пакет постоянно совершенствуется и пополняется, он хорошо зарекомендовал себя во многих организациях, в том числе активно работающих на финансовом рынке. Более подробная информация об этом пакете дана в приложениях 1 и 2, а также в [11]. Наконец, нам хотелось дать пользователям представление о более широком круге отечественных статистических пакетов.
Обзор возможностей
Возможности в области анализа временных рядов. Пользователи, знакомые с ранними и неполными версиями пакета SPSS, чаще всего имеют совершенно неадекватное представление о возможностях этого пакета в области анализа временных рядов. Во-первых, ранние версии SPSS использовались, в основном, специалистами в области психологии, биологии и социологии, где задачи анализа временных рядов менее характерны. Во-вторых, современные версии пакета имеют модульную структуру (см. приложения 1 и 2), в которой анализ временных рядов выделен в отдельный модуль SPSS Trends. При отсутствии этого модуля возможности в области анализа временных рядов будут ограничены только процедурами регрессионного анализа базового модуля пакета SPSS Base.
Кратко перечислим основные процедуры пакета SPSS в области анализа временных рядов:
- Regression (Регрессионный анализ) — позволяет выделять и удалять широкий набор моделей трендов;
- ARIMA (Модели авторегрессии-проинтегрированного скользящего среднего) — вычисляет оценки параметров для сезонных и несезонных моделей, а также строит доверительные интервалы для прогноза. Процедура допускает пропущенные значения во временных рядах и выполняет анализ интервенций;
- EXSMOOTH (Экспоненциальное сглаживание) — включает широкий круг методов экспоненциального сглаживания для сезонных и несезонных рядов с трендом;
- SEASON (Сезонные составляющие) — оценивает мультипликативные или аддитивные сезонные составляющие для сезонных временных рядов;
- SPECTRA (Спектральный анализ) — производит разложение временного ряда на гармонические составляющие. Вычисляет и выводит на график одномерную и двумерную периодограмму и оценку спектральной плотности. Позволяет использовать различные спектральные окна;
- AREG (Авторегрессионный анализ) — оценивает регрессионную модель, когда ошибки близких по времени значений ряда коррелируют между собой;
- Х11 ARIMA — оценивает сезонные факторы для процессов типа авторегрессии-проинтегрированного скользящего среднего.
Пакет также выполняет широкий круг других процедур, например, генерацию временных рядов, вычисление оценок автокорреляционной и частной автокорреляционной функции, построение различных типов графиков временных рядов и т.д.
Командный макроязык и система меню. Прежде чем начать разбор примеров в пакете SPSS, сделаем одно важное замечание. Пакет SPSS обладает развитым командным макроязыком, позволяющим создавать командные файлы, полностью описывающие все этапы анализа. Только в последних Windows-версиях пакета появилась возможность проводить почти все процедуры ввода, редактирования и анализа данных в режиме меню-ориентированного интерфейса с диалоговыми окнами. Мы ограничим свой рассказ, ориентированный на начинающих пользователей пакета, только работой с этим интерфейсом. Заодно будет проиллюстрирован довольно типичный Windows-интерфейс современных статистических пакетов. Однако, работая в SPSS, следует помнить, что при решении задачи с использованием меню-ориентированного интерфейса одновременно происходит создание командного файла решаемой задачи. Одно из удобств и достоинств командного языка заключается в том, что при решении однотипных задач нет необходимости каждый раз заполнять поля ввода и настраивать режимы работы процедур. Можно просто запускать однажды сформированный командный файл. При этом можно практически ничего не знать о самом командном языке SPSS.
Подбор тренда и прогнозирование
Рассмотрим эти задачи на следующем примере.
Пример 13.1к. Для данных урожайности зерновых культур в СССР подобрать модель тренда с помощью процедур регрессионного анализа и построить на базе подобранной модели прогноз на несколько лет вперед.
Подготовка данных. Пусть данные таблицы 1.2 находятся в текстовом (ASCII) файле zerno.txt в виде двух столбцов, первый из которых содержит значение года, а второй — значение урожайности. Для загрузки этих данных в пакет SPSS выберем в меню пакета пункт FILE, а в нем подпункт Read ASCII Data.... На экран будет выведен запрос открытия файла, его вид — такой же, как в большинстве Windows-программ. Только в нижней части запроса имеется переключатель File Format) (Формат файла), позволяющий выбирать между фиксированным (Fixed) и свободным (Freefield) форматами файла. Установим значение этого переключателя Fixed, выбрав фиксированный формат файла. Этот формат предполагает, что значения каждой переменной в строках файла записаны в тех же столбцах, что и в первой строке файла. Затем щелкнем мышью кнопку запроса | Define [ (Определить) и перейдем к определению формата записи переменных в файле.
Лекция_14
Многомерный анализ и другие статистические методы
Введение
Арсенал методов анализа данных, предлагаемых современной статистикой, разумеется, далеко не ограничивается тем, что было изложено в предыдущих главах этой книги. Так, за рамками рассмотрения остались широко используемые на практике методы многомерного статистического анализа (т.е. анализа многомерных статистических данных), а также всевозможные специализированные статистические методы, предназначенные для анализа специфических данных в конкретных предметных областях. В настоящей главе мы дадим очень краткий обзор таких методов, выбрав из них наиболее широко используемые и включенные в статистические пакеты для ЭВМ.
Замечание для профессиональных математиков и статистиков. Цель этой главы — всего лишь дать знакомящимся со статистикой читателям самое общее представление о назначении некоторых из тех областей статистики, которые не были затронуты в этой книге, а также указать список книг для дальнейшего чтения. Поэтому просим быть снисходительными к упрощениям и неточностям, неизбежным при описании сути сложных научных проблем в двух-трех абзацах.
Многомерный статистический анализ
В предыдущих главах книги мы обсуждали, в основном, такие проблемы, в которых случайная изменчивость была представлена одной (случайной) переменной. Например, у каждого наудачу выбранного объекта мы измеряли какой-то один признак; либо при каждой комбинации управляющих факторов измеряли одномерный отклик, и т.д. Исключение составила, в которой мы рассматривали вопросы связи двух (случайных) признаков. Там мы встретились с ситуацией, когда в одном эксперименте — например, при обследовании одного объекта, — измеряются сразу несколько характеристик. В таких опытах каждое наблюдение представляется не одним-единственным числом, а некоторым конечным набором чисел, в котором в заданном порядке записа




 ны все измеренные характеристики объекта. Та часть математической статистики, которая исследует эксперименты с такими многомерными наблюдениями, называется многомерным статистическим анализом.
ны все измеренные характеристики объекта. Та часть математической статистики, которая исследует эксперименты с такими многомерными наблюдениями, называется многомерным статистическим анализом.Измерение сразу нескольких признаков (свойств объектов) в одном эксперименте, в общем, более естественно, чем измерение лишь какого-то одного. Поэтому потенциально многомерный статистический анализ имеет обширное поле для применений. К тому же, с формальной точки зрения, одномерный статистический анализ (который мы и обсуждали ранее) представляет частный случай многомерного.
В настоящее время хорошо разработана математическая теория для многомерных гауссовских наблюдений, т.е. для случайных величин, подчиняющихся многомерному нормальному распределению. Здесь почти для каждого одномерного гауссовского метода существует соответствующий многомерный вариант. Кроме того, имеются решения и для некоторых специфически многомерных статистических проблем
К сожалению, построение теории для многомерных статистических данных оказалось делом весьма трудным. Такая теория до сих пор еще далеко не достигает той полноты и законченности, которая свойственна ее одномерной версии. Хорошо разработана лишь теория для гауссовских (имеющих многомерное нормальное распределение) данных. Здесь почти для каждого одномерного гауссовского статистического метода имеется соответствующий многомерный вариант. Кроме того, естественно, имеются и методы для решения некоторых специфически многомерных задач.
Построение многомерных версий для других статистических методов удается далеко не так гладко. В частности, непараметрические методы, такие важные и эффективные в одномерном случае, все еще не имеют своего законченного многомерного аналога (соответствующая теория находится в процессе разработки). Поэтому для аккуратного статистического анализа имеющихся данных нередко не находится адекватных статистических средств. Из-за этого, в частности, рассчитанные на гауссовские данные правила нередко приходится применять и там, где для этого нет достаточных оснований. Конечные выводы в таких случаях бывает нелегко интерпретировать. Более того, при анализе многомерных данных часто используют и методы, вообще не имеющие четкой статистической трактовки в духе рассмотренных ранее концепций проверки гипотез, построения доверительных интервалов и т.д. Поэтому мы не будем пытаться изложить здесь хоть сколько-нибудь цельную картину многомерного анализа, а ограничимся упоминанием и кратким пояснениями нескольких наиболее популярных методов — тех, которые уже нашли отражение в статистических пакетах.
Факторный анализ
При исследовании сложных объектов и систем (например, в психологии, биологии, социологии т.д.), часто мы не можем непосредственно измерить величины, определяющие свойства этих объектов (так называемые факторы), а иногда нам не известны даже число и содержательный смысл факторов. Для измерений могут быть доступны иные величины, тем или иным способом зависящие от этих факторов. При этом, когда влияние неизвестного фактора проявляется в нескольких измеряемых признаках, эти признаки могут обнаруживать тесную связь между собой (например, коррелированность), поэтому общее число факторов может быть гораздо меньше, чем число измеряемых переменных, которое обычно выбирается исследователем в той или иной мере произвольно. Для обнаружения влияющих на измеряемые переменные факторов используются методы факторного анализа.
В качестве примера применения факторного анализа приведем изучение свойств личности с помощью психологических тестов. Свойства личности не поддаются прямому измерению, о них можно судить только на основании поведения человека, ответа на те или иные вопросы и т.д. Для объяснения результатов проведенных опытов их результаты подвергаются факторному анализу, который и позволяет выявить те личностные свойства, которые оказывали влияние на поведение испытуемых в проведенных опытах.
Первым этапом факторного анализа, как правило, является выбор новых признаков, которые являются линейными комбинациями прежних и «вбирают» в себя большую часть общей изменчивости наблюдаемых данных, а поэтому передают большую часть информации, заключенной в первоначальных наблюдениях. Обычно это осуществляют с помощью метода главных компонент, хотя иногда используют и другие приемы (скажем, метод максимального правдоподобия). Метод главных


 компонент по существу сводится к выбору новой ортогональной системы координат в пространстве наблюдений. В качестве первой главной компоненты избирают направление, вдоль которого массив наблюдений имеет наибольший разброс, выбор каждой последующей главной компоненты происходит так, чтобы разброс наблюдений вдоль нее был максимальным и чтобы эта главная компонента была ортогональна другим главным компонентам, выбранным прежде.
компонент по существу сводится к выбору новой ортогональной системы координат в пространстве наблюдений. В качестве первой главной компоненты избирают направление, вдоль которого массив наблюдений имеет наибольший разброс, выбор каждой последующей главной компоненты происходит так, чтобы разброс наблюдений вдоль нее был максимальным и чтобы эта главная компонента была ортогональна другим главным компонентам, выбранным прежде.Однако обычно факторы, полученные методом главных компонент, не поддаются достаточно наглядной интерпретации. Поэтому следующим шагом факторного анализа служит преобразование (вращение) факторов таким образом, чтобы облегчить их интерпретацию.
Дискриминантами анализ
Предположим, что мы имеем совокупность объектов, разбитую на несколько групп (т.е. для каждого объекта мы можем сказать, к какой группе он относится). Пусть для каждого объекта имеются изменения нескольких количественных характеристик. Мы хотим найти способ, как на основании этих характеристик можно узнать группу, к которой принадлежит объект. Это позволит нам для новых объектов из той же совокупности предсказывать группы, к которой они относятся.
Например, исследуемыми объектами могут быть пациенты — здоровые или больные той или иной болезнью, а характеристиками — результаты медицинских анализов. Если мы научимся по этим характеристикам узнавать, здоров ли пациент, либо болен той или иной болезнью, это позволит значительно повысить эффективность медицинских обследований.
Для решения этой задачи применяются методы дискриминантного анализа, они позволяют строить функции измеряемых характеристик, значения которых и объясняют разбиение объектов на группы. Желательно, чтобы этих функций (дискриминирующих признаков) было немного — в этом случае результаты анализа легче содержательно истолковать. Особую роль, благодаря своей простоте, играет линейный дискриминантный анализ, в котором классифицирующие признаки выбираются как линейные функции от первичных признаков. В случае разделения нескольких нормальных (гауссовских) совокупностей линейный дискриминантный анализ имеет ясные статистические свойства.
Лекция_15
Кластерный анализ
Методы кластерного анализа позволяют разбить изучаемую совокупность объектов на группы «схожих» объектов, называемых кластерами.
Большинство методов кластеризации (иерархической группировки) являются аггломеративными (объединительными) — они начинают с создания элементарных кластеров, каждый из которых состоит ровно из одного исходного наблюдения (одной точки), а на каждом последующем шаге происходит объединение двух наиболее близких кластеров в один. Момент остановки этого процесса может задаваться исследователем (например, указанием требуемого числа кластеров или максимального расстояния, при котором допустимо объединение). Графическое изображение процесса объединения кластеров моет быть получено с помощью дендрограммы — дерева объединения кластеров. Другие методы кластерного анализа являются дивизивными — они пытаются разбивать объекты на кластеры непосредственно.
Методы кластеризации довольно разнообразны, в них по-разному выбирается способ определения близости между кластерами (и между объектами), а также используются различные алгоритмы вычислений. Заметим, что результаты кластеризации зависят от выбранного метода, и эта зависимость тем сильнее, чем менее явно изучаемая совокупность разделяется на группы объектов. Поэтому результаты вычислительной кластеризации могут быть дискуссионными и часто они служат лишь подспорьем для содержательного анализа.
Заметим также, что методы кластерного анализа не дают какого-либо способа для проверки статистической гипотезы об адекватности полученных классификаций. Иногда результаты кластеризации можно обосновать с помощью методов дискриминантного анализа.
