Методические рекомендации для студентов по изучению дисциплины 29 1

Вид материала

Методические рекомендации

Содержание I. Мотивация изучения темы. II. Задание открытого типа III. Решение проблемы участниками семинарского занятия. IV. Демонстрация образовательных продуктов. V.Организация рефлексивной деятельности студентов на заключительном этапе семинарского занятия. I. Мотивация изучения темы. II. Задание открытого типа III. Решение проблемы участниками семинарского занятия. IV Демонстрация образовательных продуктов. I. Мотивация изучения темы. II. Формулирование учебного (открытого) задания по решению поставленной проблемы. III. Решение проблемы студентами – участниками семинарского занятия. IV. Демонстрация образовательных продуктов. V. Организация рефлексивной деятельности. I. Мотивация изучения темы. А есть подмножество В В должна быть выполнима операция, которая в А II.Формулирование учебного (открытого) задания по решению поставленной проблемы. III. Решение проблемы студентами – участниками семинарского занятия. IV. Демонстрация образовательных продуктов. ... Полное содержание

Подобный материал:

• Методические рекомендации по изучению дисциплины для студентов специальностей 240701, 306.81kb.
• Методические рекомендации по изучению дисциплины теория организации для студентов, 442.62kb.
• Рекомендации к изучению дисциплины и выполнению, 513.35kb.
• Методические рекомендации по изучению дисциплины основы рекламного менеджмента для, 314.99kb.
• Методические рекомендации по изучению дисциплины для студентов Н. Новгород, 380.41kb.
• О. И. Быльченко Методические рекомендации по изучению курса «Отечественная история», 924.46kb.
• Методические указания по изучению дисциплины и задание для контрольной работы для студентов-заочников, 328.95kb.
• Методические рекомендации для студентов и слушателей по изучению курса Конституционное, 316.95kb.
• Методические рекомендации к изучению дисциплины по дисциплине Ценообразование название, 123.21kb.
• Методические рекомендации к изучению курса для студентов юридического факультета Калининград, 413.15kb.

Тема: «Организация самостоятельной работы
при обучении учащихся математике»

I. Мотивация изучения темы.

Традиционное обучение вооружает учащихся готовыми знаниями. При этом самостоятельная работа представляется, в основном, как репродуктивная деятельность. Обучение, ориентированное на личностное развитие учащихся, предполагает конструирование учениками собственного смысла, целей и содержания образования, а также процесса его организации, осознания. В любой модели обучения, получаемые знания не должны быть формальными, знания должны быть осознанными. Согласно выводам психолого-педагогических исследований, осознание знаний осуществляется только в самостоятельной учебной деятельности когнитивного, креативного, организационного характера. Как организовать самостоятельную работу учащихся в условиях современной школы при обучении математике?

Решению этой проблемы посвящено это семинарское занятие.

II. Задание открытого типа: разработать методические рекомендации по организации самостоятельной учебной деятельности учащихся:

а) когнитивного типа (наблюдение, эксперимент, исследование объекта, проведение лабораторной работы, работа с книгой, работа по образцу и др.);

б) креативного типа (изобретательство, фантазия, открытия, сочинения, моделирование, составление задач, вопросов, творческих заданий и др.);

в) организационного типа (целеполагание, нормотворчество, групповая работа, рефлексия, рецензирование и др.).

III. Решение проблемы участниками семинарского занятия.

Выполняя сформулированное выше задание открытого типа, каждый студент по желанию выбирает организацию самостоятельной работы учащихся по указанным видам учебной деятельности креативного, когнитивного и организационного характера. Подготовку к семинару он осуществляет как выполнение домашней самостоятельной работы. Доклад-сообщение может быть оформлен в форме тезисов или полного текста выступления. В докладе подробно излагается смысл, сущность самостоятельной работы, подробная методика её организации и проведения с учащимися на конкретном учебном материале школьного курса математики.

IV. Демонстрация образовательных продуктов.

Подготовленные методические рекомендации по организации самостоятельной работы учащихся следует изложить устно на семинарском занятии при этом использовать заранее подготовленные таблицы, модели, компьютерные презентации.

После прослушивания доклада сокурсника осуществить рецензирование:

а) полно ли раскрыта тема;

б) что понравилось в выступлении;

в) замечания, возражения выступающему;

г) дополнения, замечания, пожелания выступающему.

Например, после доклада – сообщения «Жизнь в стране плоскатиков» задать вопросы:

1. Сочинение, которое вы зачитали, действительно написал ученик?

2. Как учитель участвует в написании таких сочинений?

Целесообразно высказать пожелания докладчику: разработать возможные общие схемы других 2-3х сочинений школьников по данной теме.

V.Организация рефлексивной деятельности студентов на заключительном этапе семинарского занятия. Рефлексия осуществляется в диалогическом общении преподавателя и студентов.

Прекращаются все выступления (доклады) студентов.

Восстанавливается последовательность прослушанных докладов.

Проводится анализ докладов, выступлений студентов с точки зрения их адекватности, продуктивности.

Формулируются результаты рефлексии.

Например, на семинарском занятии большое внимание уделено организации самостоятельной работы когнитивного типа: работе с учебником, работе по образцу, исследованию объекта. Недостаточно разработана методика организации самостоятельной работы креативного типа.

VI. Список литературы:

1. Методика преподавания математики [Текст] / Сост. : Р.С. Черкасов, А.А. Столяр. – М. : Просвещение, 1986. -336 c.
   
2. Хуторской, А.В. Развитие одарённости школьников: Методика продуктивного обучения. [Текст] / Хуторской А.В. – М: Владос, 2000. -544 c.
   
3. Зайцева, Г.Д. Организация творческих образовательных ситуаций при обучении математике учащихся средней школы./ Зайцева Г.Д. – Бийск, РИО БПГУ им. В.М.Шукшина, 2005. -88 c.
   
4. Учебники по математике для средней школы.
   
5. Зайцева, Г.Д. Создание и разрешение образовательных ситуаций на семинарских занятиях при изучении курса ТиМОМ [Текст]: методические рекомендации для студентов / Г.Д. Зайцева, А.И. Исаева. – Бийск: РИО БГПУ им. В.М. Шукшина , 2009. -69 с.
   

Домашнее задание: изучить инструкцию по организации и проведению семинарского занятия №2, выполнить задание открытого типа №2 ( см. [5] c. 10-19).

§2. Семинарское занятие № 2

Тема: «Индивидуализация и дифференциация
при обучении математике учащихся средней школы»

I. Мотивация изучения темы.

Одной из главных целей личностно- ориентированного обучения является одновременность реализации персональных моделей образования учащихся. Для этого каждому ученику необходимо предоставить возможность собственной образовательной траектории освоения всех учебных дисциплин , в частности, математики. Ученик должен получить право на индивидуальный смысл и цели обучения, опережение и углубление учебного материала, выбор темпа, форм и методов обучения. Задача учителя – в обеспечении индивидуальной зоны творческого развития каждого ученика. Одновременность реализации персональных моделей образования – одна из целей образования в старшей профильной школе. Однако нельзя допустить, чтобы старшие профильные классы были образованы из учеников традиционной школы, не получивших элементарных навыков продуктивной деятельности, осуществления целеполагания, рефлексии, выбора опережения, углубления в изучении математики.

Следует заметить, что на начальном этапе перехода на личностно-ориентированное обучение не удаётся реализовать этот принцип полностью по причине высокой наполняемости классов, отсутствия у учителей опыта организации такой учебной работы. На этапе предпрофильного обучения целесообразно использовать разноуровневый подход к обучению. Каждая группа учащихся при освоении одной и той же темы работает с учётом своих возможностей. Уровневая система обучения даёт возможность ученику самому выбрать форму самостоятельной работы, определить уровень знаний, метод изучения учебного материала. Как организовать разноуровневое обучение математике учащихся в условиях современной (традиционной!) школы. Решению этой проблемы посвящено это семинарское занятие.

II. Задание открытого типа: разработать методические рекомендации по использованию разноуровнего подхода в обучении математике учащихся средней школы:

1. при освоении нового материала;
   
2. при обучении решению математических задач;
   
3. при проведении обобщающих уроков математики;
   
4. при организации контроля знаний.
   

При подготовке проектов использовать информационные и коммуникационные технологии обучения.

III. Решение проблемы участниками семинарского занятия.

При выполнении открытого задания каждому студенту выбрать организацию проекта разноуровнего подхода в обучении из указанных направлений а), б), в), г) или предложить свой проект.

Разработку проекта осуществить в форме тезисов или подробного доклада.

IV Демонстрация образовательных продуктов.

Осуществляется прослушивание студенческих докладов-проектов об организации разноуровнего обучения математике учащихся средней школы. Длительность доклада 5-7 минут. При выступлении используются заранее подготовленные таблицы, модели, компьютерные презентации.

После окончания доклада сокурсники должны:

1. задать вопросы выступающему;
   
2. отметить положительные качества разработанной методики;
   
3. высказать замечания, возражения, дополнения, пожелания докладчику.
   

Например, после докладов-сообщений приведенных выше целесообразно высказать пожелания докладчику: использование современных информационных и коммуникационных технологий повысит эффективность разработанных методических рекомендаций.

V. Организация рефлексивной деятельности на заключительном этапе семинарского занятия:

1. прекратить все выступления, доклады, сообщения;
   
2. восстановить последовательность докладов;
   
3. провести анализ докладов, выступлений студентов с точки зрения их эффективности продуктивности;
   
4. сформулировать результаты рефлексии.
   

Например, на семинарском занятии большое внимание уделено рассмотрению методики разноуровнего подхода при изучении нового материала. Почти не уделено внимание организации разноуровнего контроля знаний. На одном из занятий по ТиМОМ (лабораторном, семинарском, лекционном) к этому вопросу следует вернуться и разрешить его.

VI. Список литературы:

1. Якиманская, И.С. Дифференцированное обучение: «внешние» и «внутренние» формы [Текст]/ И.С. Якиманская // Хрестоматия по педагогике, ч. II - Барнаул, 1999. – С. 46-49.
   
2. Хуторской, А.В. Современная дидактика [Текст] / А.В. Хуторской, - СПб: Питер, 2001. – 544 с.
   
3. Зайцева, Г.Д. Эвристическое обучение математике./ Г.Д. Зайцева; Бийский пед. гос. ун-т им. В. М. Шукшина. – Бийск: РИО БПГУ им. В. М. Шукшина, 2008. – 81 с.
   
4. Учебники по математике для средней школы.
   
5. Зайцева, Г.Д. Создание и разрешение образовательных ситуаций на семинарских занятиях при изучении курса ТиМОМ [Текст]: методические рекомендации для студентов / Г.Д. Зайцева, А.И. Исаева. – Бийск: РИО БГПУ им. В.М. Шукшина , 2009. -69 с.
   

Домашнее задание: изучить инструкцию по организации и проведению семинарского занятия №3, выполнить задание открытого типа №3 ( см. [5] с. 19-24).

§3. Семинарское занятие № 3

Тема: «Проверка знаний, умений и навыков,
учащихся по математике»

I. Мотивация изучения темы. Проблематизация учебной деятельности. Создание образовательной напряженности.

Образовательная диагностика – это процесс определения результатов образовательной деятельности учащихся и учителя с целью выявления недостатков, анализа, оценивания и корректировки обучения.

В состав диагностики входят различные формы контроля, который означает выявление, измерение и оценивание знаний, умений и навыков учеников. Выявление и измерение называют проверкой. Оценка – это процесс, деятельность по оцениванию. Отметка – результат процесса оценивания.

В обучении применяются следующие виды контроля: предварительный, текущий, повторный, периодический, итоговый.

В традиционной системе обучения контролю подлежат знания, умения и навыки учащихся, которые проверяются с помощью известных приёмов учебной работы: контрольных работ, зачётов, экзаменов. Объектом контроля при этом является внешне заданное содержание образования, независимо от учителя и ученика.

Оценивание в традиционной школе – это сравнение достижений ученика с внешними образовательными стандартами.

При личностно-ориентированном подходе к обучению проверяются не только предметные знания, умения и навыки, но и усвоение детьми способов деятельности, развитие способностей, творческая продукция учеников.

Как осуществлять проверку, оценивание образовательных результатов в личностно-ориентированном обучении учащихся?

Рассмотрению этой проблемы посвящено это семинарское занятие.

II. Формулирование учебного (открытого) задания по решению поставленной проблемы.

Разработать методику и технологии по организации проверки развития способностей учащихся по освоению способов образовательной деятельности: когнитивной, креативной, организационной, коммуникативной, при изучении школьного курса математики. Тема выбирается студентами по желанию.

III. Решение проблемы студентами – участниками семинарского занятия.

Подготовка творческих методических разработок по осуществлению проверки освоения школьниками способов образовательной деятельности проводится в ходе выполнения домашнего задания.

IV. Демонстрация образовательных продуктов.

Непосредственно на семинарском занятии студенты выступают с сообщением о результатах своих методических исследований по проблеме семинара, осуществляется обсуждение докладов (дополнения, замечания, предложения, оценивание методик и технологий).

V. Организация рефлексивной деятельности.

Формулирование полученных результатов.

Например, так: проверку овладения способами образовательной деятельности нужно осуществлять в процессе этой деятельности. При этом необходимо определить степень образовательного приращения ученика в овладении этой деятельностью (понимание этапов деятельности, самостоятельность осуществления этих этапов, использование образовательной деятельности в новых условиях).

Выражение неудовлетворенности содержанием некоторых докладов. Например, о содержании доклада по проверке овладением поисково-исследовательской деятельностью можно высказать идею, о необходимости рассмотрения ещё одного примера фрагмента урока, где учащиеся свободно владеют поисково-исследовательской деятельностью.

Определение целей дальнейшей учебной работы.

При организации проверки знаний, умений и навыков учащихся нельзя ограничиваться проверкой только знаний, умений и навыков по математике. Целесообразно осуществлять контроль за освоением способов образовательной деятельности (когнитивной, креативной, организационной, коммуникативной), осуществляя наблюдение за ростом степени образовательного приращения учеников по каждому виду деятельности.

VI. Список литературы:

1. Учебники алгебры за 7-9 классы.
   
2. Хуторской, А.В. Развитие одарённости школьников: Методика продуктивного обучения. [Текст]/ Хуторской, А.В. – М: Владос, 2000. -544 с.
   
3. Научно-теоретический и методический журнал «Математика в школе».
   
4. Учебно-методическая газета «Математика».
   
5. Зайцева, Г.Д. Создание и разрешение образовательных ситуаций на семинарских занятиях при изучении курса ТиМОМ [Текст]: методические рекомендации для студентов / Г.Д. Зайцева, А.И. Исаева. – Бийск: РИО БГПУ им. В.М. Шукшина , 2009. -69 с.
   

Домашнее задание: изучить инструкцию по организации и проведению семинарского занятия №4, выполнить задание открытого типа №4 ( см. [5] с. 25-31).

§4. Семинарское занятие № 4

Тема: «Методика изучения числовых множеств

и действий над ними»

I. Мотивация изучения темы. Проблематизация учебной деятельности. Создание образовательной напряженности.

Н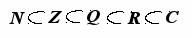атуральные числа являются фундаментом, на котором строятся все другие числовые множества. При этом всякое новое числовое множество является расширением предыдущего, так что обобщение понятия числа происходит по схеме


При любой схеме обобщения понятия числа строятся расширения, обладающие определёнными свойствами по отношению к расширяемому множеству. Если, например, множество А расширяется до множества В, то построение расширения должно удовлетворять следующим условиям:

1. А есть подмножество В.

2. Отношения и операции для элементов множества В, раннее известные для множества А, должны быть определены так, чтобы их смысл для элементов из А, рассматриваемых как элементы из В, совпадал с тем, какой они имели в А до расширения.

3. Во множестве В должна быть выполнима операция, которая в А была невыполнима или не всегда выполнима.

4. Расширение В должно быть минимальным из всех возможных расширений множества А, удовлетворяющих требованиям 1-3.

В школьном преподавании более распространенным является построение множества В присоединением к элементам множества А некоторых новых элементов.

Введение новых чисел при всех расширениях обосновывается потребностями самой математики, потребностями практики, жизни.

Какова методика изучения числовых множеств в средней школе?

Решению этой проблемы посвящено это семинарское занятие.

II.Формулирование учебного (открытого) задания по решению поставленной проблемы.

Разработать методику и технологии изучения числовых множеств (натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел, действительных чисел) в основной школе с использованием методики сотрудничества учителя и учащихся. Тема проекта-доклада выбирается студентом и согласовывается с преподавателем.

III. Решение проблемы студентами – участниками семинарского занятия.

Разработка методик и технологий изучения числовых систем в основной школе с использованием сотрудничества учителя и учащихся проводится в ходе выполнения домашнего задания. При этом изучается учебно-методическая литература, рекомендованная преподавателем, дополнительные сведения по теме найденные в Интернете, а также используется содержание текста лекций по ТиМОМ, соответствующее теме.

IV. Демонстрация образовательных продуктов.

На семинарском занятии студенты выступают с докладами о результатах своей творческой методической работы. Длительность доклада не более 7-8 минут, чтобы дать возможность выступить многим студентам. При этом активно используются компьютерные презентации, слайды, бумажные плакаты-таблицы, заранее подготовленный дидактический материал.

Осуществляется обсуждение докладов (дополнения, замечания, предложения, оценивание разработанных рекомендаций).

Например, по приведенному выше докладу о методике изучения действительных чисел возможны замечания:

1. автор доклада не уделил внимания методике изучения действий над действительными числами, хотя этот учебный материал имеет свои особенности и трудности;
   
2. автор доклада использовал в своей методике технологии личностно-развивающего обучения, не получили явной реализации принципы личностно-ориентированного обучения;
   
3. слабо использовались возможности компьютерной техники.
   

V. Организация рефлексивной деятельности.

Формулирование полученных выводов: систематизация методических приемов изучения числовых множеств.

Выражение неудовлетворённости содержанием некоторых сообщений. Например, недостаточно полно разрабатывалась и применялась организация образовательных ситуаций с использованием заданий открытого типа.

Определение целей домашней работы: при разработке методик изучения числовых множеств при проведении уроков стремиться к реализации основных принципов личностно-ориентированного обучения.

VI. Список литературы:

1. Виленкин, Н.Я. Математика 6.[Текст]/ Н.Я. Виленкин и др.- М.:Мнемозина, 2005. -288 с.
   
2. Алгебра 8. Под редакцией С.А. Теляковского. – М., 1991. -223 с.
   
3. Мордкович, А.Г. Алгебра 8 .[Текст]/ А.Г. Мордкович.– М., 2001. -227 с.
   
4. Лященко, Е.И. Методика обучения математике.[Текст]/ Лященко, Е.И., Мазаник А.А. – Минск, 1976. -222 с.
   
5. Новик, И.А. Практикум по методике преподавания математики. .[Текст]/ И.А. Новик. – Минск, 1984. -175 с.
   
6. Научно-теоретический и методический журнал «Математика в школе»
   
7. Учебно-методическая газета «Математика»
   
8. Хуторской, А.В. Современная дидактика [Текст] / А.В. Хуторской, - СПб: Питер, 2001. -544 с.
   
9. Зайцева, Г.Д. Эвристическое обучение математике./ Г.Д. Зайцева; Бийский пед. гос. ун-т им. В. М. Шукшина. – Бийск: РИО БПГУ им. В. М. Шукшина, 2008. -81 с.
   
10. Зайцева, Г.Д. Создание и разрешение образовательных ситуаций на семинарских занятиях при изучении курса ТиМОМ [Текст]: методические рекомендации для студентов / Г.Д. Зайцева, А.И. Исаева. – Бийск: РИО БГПУ им. В.М. Шукшина , 2009. -69 с.
    

Домашнее задание: изучить инструкцию по организации и проведению семинарского занятия №5, выполнить задание открытого типа №5 ( см. [10] с. 31-35).


§5. Семинарское занятие № 5

Тема: «Методика изучения комплексных чисел

в средней школе»

I. Мотивация изучения темы. Проблематизация учебной деятельности. Создание образовательной напряженности.

Изучение комплексных чисел является завершающим этапом построения числовых систем в школьном курсе математики. Однако на современном этапе в общеобразовательной школе эта тема является резервной. По мере переработки учебников при наличии необходимого времени она планируется в качестве обязательной в 10-11 классах средней школы.

Следует отметить, что традиционное изучение комплексных чисел имеет резко выраженный формальный характер. Отметим два коренных недостатка, характерных для традиционного изучения.

На всех этапах расширения понятия числа введение новых чисел всегда заботливо связывалось с той материальной базой, которая побуждала ввести числа новой природы. Появление новых чисел оказывалась в глазах учеников оправданным и естественным.

Иначе дело обстоит с мнимыми числами. Первая встреча ученика с комплексными числами происходит, когда без предварительной подготовки на одном из уроков появляется таинственное число i, а затем и символ a+bi. Что отображает это число, какие стороны практики? Ученикам не ясно! Учащиеся смотрят на него как на произвольно возникшее формальное изобретение.

Второй коренной недостаток связан с тем, что в символе a+bi никак не оправданы действия сложения и умножения. Учащимся предлагается рассматривать эти действия, как операции само собой разумеющиеся.

Полностью преодолеть формальный характер изложения и изучения комплексных чисел в школе невозможно, но существенно ослабить чрезмерный формализм вполне возможно. Эта задача и составляет основную методическую проблему, решению которой будет посвящено это семинарское занятие.

II. Задание открытого типа: разработать проекты методик изучения комплексных чисел в средней школе с реализацией основных принципов развивающего обучения. При этом рассмотреть следующие темы.

1. Постановка задачи о необходимости расширения поля действительных чисел.

Методика введения алгебраической формы комплексных чисел. Геометрическое изображение комплексных чисел.

2. Методика изучения действий над комплексными числами в алгебраической форме.

3. Тригонометрическая форма комплексных чисел. Методика изучения действий над комплексными числами в тригонометрической форме.

При разработке проектов методических рекомендаций целесообразно использовать компьютерные презентации, слайды, бумажные таблицы, карточки и т.п.

III. Решение проблемы студентами – участниками семинарского занятия.

С темой и проблемой данного семинарского занятия №8 студенты знакомятся ещё при занятии №7 при обсуждении домашнего задания. При этом они уже имеют достаточный опыт учебной деятельности при подготовке к очередному семинарскому занятию: каждый студент выбирает тему будущего проекта по методике изучения комплексных чисел и согласовывает её с преподавателем, знакомится с мотивацией решения общей проблемы, уясняет личностный смысл своей учебной исследовательской работы над выбранной темой. Далее изучается и анализируется математическая, методическая, педагогическая литература, рекомендованная преподавателем. При необходимости студент должен уметь отыскать дополнительную информацию в Интернете.

Будущий проект методических рекомендаций по выбранной теме должен содержать в себе элементы методики личностно-развивающего или личностно-ориентированного обучения.

IV. Демонстрация образовательных продуктов.

На этом этапе непосредственно на семинарском занятии в студенческой аудитории осуществляется защита проектов по методике изучения комплексных чисел. Каждое выступление сопровождается компьютерными презентациями, демонстрацией слайдов, таблиц, карточек и т.п.

После каждого выступления студента проводится дискуссия (задаются вопросы, высказываются замечания, дополнения).

V. Организация рефлексивной деятельности.

После окончания защиты всех проектов по методике изучения комплексных чисел проводится анализ методических рекомендаций с точки зрения их эффективности, продуктивности. Осуществляется целеполагание к организации дальнейшей образовательной деятельности по разработке методик и технологий обучения учащихся математике в современной школе.

VI. Список литературы:

1. Кочетков, Е.С. Кочеткова Е.С. Алгебра и элементарные функции. [Текст] Учебное пособие для 10 класса/ Кочетков Е.С., Кочеткова Е.С – М. 1970. -267 с.
   
2. Методика преподавания математики в средней школе. Частная методика. .[Текст] / Под ред. В.И. Мишина – М. 1987. -416 с.
   
3. Репкина, Н.В. Что такое развивающее обучение. .[Текст] / Репкина Н.В. – Томск: Пеленг, 1993. -117 с.
   
4. Зайцева, Г.Д. Использование современных дидактических концепций при обучении учащихся на уроках математики в средней школе. [Текст]. / Г.Д. Зайцева; Бийский пед. гос. ун-т им. В. М. Шукшина. – Бийск: РИО БПГУ им. В. М. Шукшина, 2008. -89 с.
   
5. Хуторской, А.В. Современная дидактика [Текст] / А.В. Хуторской, - СПб: Питер, 2001. -544 с.
   
6. Зайцева, Г.Д. Создание и разрешение образовательных ситуаций на семинарских занятиях при изучении курса ТиМОМ [Текст]: методические рекомендации для студентов / Г.Д. Зайцева, А.И. Исаева. – Бийск: РИО БГПУ им. В.М. Шукшина , 2009. -69 с.
   

Домашнее задание: изучить инструкцию по организации и проведению семинарского занятия №6, выполнить задание открытого типа №6 ( см. [6] с. 36-41).

§6. Семинарское занятие № 6