Методические рекомендации для студентов по изучению дисциплины 29 1

Вид материала

Методические рекомендации

Содержание V семестр VII семестр Домашняя индивидуальная контрольная работа Домашняя индивидуальная контрольная работа Общая методика 3. Методические рекомендации для студентов Объектом МОМ Термин «понятие» применяется для обозначения мысленного класса объектов реальной действительности и нашего сознания Способы введения Система требований Цели урока Анализ урока

Подобный материал:

• Методические рекомендации по изучению дисциплины для студентов специальностей 240701, 306.81kb.
• Методические рекомендации по изучению дисциплины теория организации для студентов, 442.62kb.
• Рекомендации к изучению дисциплины и выполнению, 513.35kb.
• Методические рекомендации по изучению дисциплины основы рекламного менеджмента для, 314.99kb.
• Методические рекомендации по изучению дисциплины для студентов Н. Новгород, 380.41kb.
• О. И. Быльченко Методические рекомендации по изучению курса «Отечественная история», 924.46kb.
• Методические указания по изучению дисциплины и задание для контрольной работы для студентов-заочников, 328.95kb.
• Методические рекомендации для студентов и слушателей по изучению курса Конституционное, 316.95kb.
• Методические рекомендации к изучению дисциплины по дисциплине Ценообразование название, 123.21kb.
• Методические рекомендации к изучению курса для студентов юридического факультета Калининград, 413.15kb.

2.1. Карта рейтинг-контроля

успеваемости студентов по дисциплине

«Теория и методика обучения математике»

для студентов образовательной профессиональной программы

050201.62 («Математика» с дополнительной специальностью «Информатика»)


V семестр

Точка 1		Дата		Вес точки 40%							Дата	Вес точки 60%				Итоговый процент				Оценка по рейтин-гу	Дата	Итог	Подпись препо- давателя
Процент выполнения				Итоговый процент								Итоговый процент									Зачет
Лек.	Пр.		Лаб.	60%	75%	85%	100%	Лек.	Пр.	Лаб.	К.р.	60%	75%	85%	100%	60%	75%	85%	100%
5%	10%		25%					5%	10%	20%	25%

VII семестр

Точка 1	Дата		Вес точки 40%				Точка 2		Дата	Вес точки 60%				Итоговый процент				Оценка по рейтингу	Дата	Итог	Подпись препо- давателя
Процент выполнения			Итоговый процент				Процент выполнения			Итоговый процент									Экза-мен
Лек.		Лаб.	60%	75%	85%	100%	Лек.	Лаб.	К.р.	60%	75%	85%	100%	60%	75%	85%	100%
10%		30%					10%	20%	30%

2.2 Контрольно-измерительные материалы по дисциплине «Теория и методика обучения математике»

Содержание контрольных работ по ТиМОМ по семестрам

V семестр, III курс

Домашняя индивидуальная контрольная работа

Составить полный план­конспект урока с использованием элементов методики развивающего обучения и информационных технологий по темам:

Уравнение (5 класс).

Деление обыкновенных дробей (6 класс).

Умножение натуральных чисел (5 класс).

Сложение дробей с разными знаменателями (6 класс).

Вычитание натуральных чисел ( 5 класс).

Деление натуральных чисел (5 класс). Основное свойство дроби (6 класс). Введение десятичных дробей (5 класс).

Сложение двух чисел с разными знаками (6 класс).

Угол (5 класс).

Процент (5 класс).

Вычитание положительных и отрицательных (6 класс).

Умножение десятичных дробей (5 класс).

Умножение положительных и отрицательных чисел (6 класс).

Деление на десятичную дробь (5 класс).

Деление обыкновенных дробей ( 6 класс ).

Сокращение дробей (6 класс).

Сравнение обыкновенных дробей (6 класс).

Среднее арифметическое (5 класс).

Нахождение дроби от числа (6 класс).

Тождества (7 класс).

График функции (7 класс).

Линейная функция и ее график (7 класс). Функция _у=х ² и ее график (7 класс).

Умножение одночлена на многочлен (7 класс).

Вынесение общего знаменателя за скобки (7 класс).

Умножение многочлена на многочлен (7 класс). Доказательство тождеств (7 класс).

Возведение в квадрат суммы и разности двух выражений (7 класс).

Разложение на множители с помощью формул квадрата суммы и квадрата разности (7 класс).

Умножение разности двух выражений на их сумму (7 класс). Разложение разности квадратов на множители (7 класс). Разложение на множители суммы и разности кубов (7 класс). Системы линейных уравнений с двумя переменными (7 класс). Решение систем линейных уравнений. Способ подстановки. Решение систем линейных уравнений. Способ сложения.

Числовые неравенства. Свойства числовых неравенств (1­ый урок) (8 класс).

Решение неравенств с одной переменной (8 класс).

Решение квадратных уравнений выделением квадрата двучлена (8 класс).

Графический способ решения уравнений (8 класс).

VII cеместр, IV курс

Домашняя индивидуальная контрольная работа

Разработать методический проект с использованием современных информационных и коммуникационных технологий эвристического обучения по данной вам теме:

^{Методика изучения функции} _у=ах ² _+bx+c <sup>(9 класс).

Методика изучения функции</sup> _у=х ^{п , где п = N (9 класс).}

Методика изучения простейших геометрических построений(7 класс).

Методика изучения второго признака подобия треугольников.

Методика изучения поворота(на плоскости). Методика изучения осевой симметрии. Методика изучения темы «Равенство фигур».

Методика изучения темы «Сумма углов треугольника». Методика изучения темы «Координаты вектора». Методика изучения темы «Сложение векторов».

Методика изучения темы «Окружность, описанная около треугольника».

Методика изучения площади параллелограмма. Методика изучения площади трапеции. Методика изучения темы «Длина окружности». Методика изучения линейной функции.

Методика построения сечений многогранников плоскостью. Метод внутреннего проектирования.

Методика изучения признака параллельности плоскостей.

Методика изучения признака перпендикулярности прямой и плоскости.

Методика изучения логарифмической функции. Методика изучения тригонометрических неравенств. Объем наклонной призмы.

Площадь сферы.

Объем конуса.

Объем пирамиды.

Признаки возрастания и убывания функции.

Методика работы над решением задачи №47, §21(учебник А.В.Погорелова «Геометрия 7­11»).

Программы зачетов и экзаменов по ТиМОМ

V cеместр, III курс Программа зачета по ТиМОМ

Общая методика

• Современные теории обучения. Личностно­развивающее обучение и его основные принципы.
  

• Методы обучения. Научные методы исследования в обучении математике. Современные информационные и коммуникационные технологии обучения.
  

• Методика изучения математических понятий, аксиом и теорем, умственных действий.
  

• Задачи – цель и средство в обучении математике.
  

• Урок – основная форма обучения математике. Культура современного урока.
  
• Нетрадиционные формы проведения уроков математики.
  
• Средства обучения математике.
  

• Организация самостоятельной работы учащихся, повторения и проверки учебного материала с использованием информационных технологий.
  
• Индивидуализация и дифференциация обучения математике.
  
• Организация внеклассной работы по математике.
  
• Составление фрагмента плана­конспекта урока математики.
  

Специальная методика

• Методика изучения натуральных чисел.
  
• Методика изучения десятичных дробей.
  
• Методика изучения положительных и отрицательных чисел.
  
• Методика изучения обыкновенных дробей.
  
• Методика введения понятия функции.
  
• Методика изучения линейной функции.
  
• Методика изучения уравнений и неравенств в 7­9 классах.
  
• Методика изучения квадратичной функции.
  
• Методика изучения действительных чисел.
  
• Методика изучения степенной функции.
  
• Методика проведения первых уроков геометрии. Логическое строение школьного курса геометрии.
  
• Методика изучения тождественных преобразований алгебраических выражений.
  
• Методика изучения геометрических построений в 7­9 классах.
  
• Методика изучения геометрических преобразований(движений).
  
• Методика изучения подобия.
  
• Методика изучения темы «Многоугольники».
  
• Методика изучения темы «Равенство фигур».
  
• Методика изучения темы «Окружность. Круг».
  
• Методика изучения темы «Векторы».
  
• Методика изучения площадей.
  
• Методика изучения прогрессий.
  

VII cеместр, IV курс

Программа экзамена по ТиМОМ

• Методика изучения комплексных чисел в средней школе.
  
• Методика проведения первых уроков стереометрии.
  
• Методика изучения параллельности и перпендикулярности прямых и плоскостей.
  
• Методика обучения решению задач на построение в стереометрии.
  
• Методика изучения темы «Многогранники».
  
• Методика изучения тригонометрических, показательной, логарифмической функций.
  
• Методика обучения решению тригонометрических, показательных, логарифмических уравнений и неравенств.
  
• Методика введения производной функции.
  
• Производные элементарных функций и методика их изучения.
  
• Методика обучения исследованию функций в средней школе.
  
• Методика изучения интеграла.
  
• Методика обучения решению задач векторно­координатным способом.
  
• Методика изучения темы «Тела вращения».
  
• Методика изучения объемов в школьном курсе геометрии.
  
• Методика обучения решению задач на комбинации многогранников и тел вращения.
  

3. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ СТУДЕНТОВ

3.1. Тезисы лекций по курсу ТиМОМ

ЛЕКЦИЯ №1 (Тезисы)

Предмет, цели и задачи курса

«Теория и методика обучения математике».

Цели обучения математике в школе. Принципы обучения.

Содержание школьного курса математики

Методологическую основу ТиМОМ составляют математика, философия, педагогика, психология.

ТиМОМ состоит из трех основных частей:

общая методика, специальная методика, конкретная методика.

Объектом МОМ является процесс обучения математике в школе.

Предметом МОМ являются методические системы обучения математике в школе (содержание, методы, формы, средства обучения математике, деятельность учителя по проектированию учебного процесса).

Цели обучения математике в школе:

• воспитание личности, интеллектуальное развитие учащихся;
  
• овладение математическими знаниями;
  
• формирование представлений об идеях и методах математики.
  

Принципы обучения  это важнейшие требования к организации процесса обучения. Система дидактических принципов: принцип воспитания и развития личности учащихся; принцип научности; принцип сознательности, активности и самостоятельности; принцип систематичности, принцип доступности; принцип наглядности; принцип дифференцированного обучения; принцип прочности знаний.

Содержание школьного курса математики составляют следующие математические разделы: числа и вычисления, выражения и их преобразования, уравнения и неравенства, функции, геометрические фигуры, тела и их свойства, начала математического анализа.

Литература:

1. Методика преподавания математики в средней школе [Текст]: Общая методика / Сост. Р.С. Черкасов, А.А. Столяр  М.: Просвещение, 1985. -336 с.
   
2. Владимирцева, С.А. Теория и методика обучения математике [Текст]: Общая методика / С.А. Владимирцева  Барнаул: Изд-во БПГУ, 2005. -158 с.
   
3. Методика и технология обучения математике. [Текст]: Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №2 (Тезисы)

Методы обучения математике.

Основные методические системы обучения в школе


Метод обучения  это способ взаимосвязанной деятельности учителя и учащихся, направленный на решение задач обучения.


По степени познавательной активности учащихся методы классифицируются: догматические, репродуктивные, объяснительно-иллюстративные, продуктивные, частично-поисковые, исследовательские.

В организации современного процесса обучения выделяют несколько методических систем обучения:

• традиционное обучение,
  
• дифференцированное обучение,
  
• проблемное обучение,
  
• личностно-ориентированное обучение.
  

Литература:

1. Методика преподавания математики в средней школе. Общая методика. [Текст] / Р.С. Черкасов, А.А. Столяр  М.: Просвещение, 1986. -336 с.
   
2. Владимирцева, С.А. Теория и методика обучения математике. Общая методика [Текст] / С.А. Владимирцева  Барнаул: Изд-во БПГУ, 2005. -158 с.
   
3. Хуторской А.В. Практикум по дидактике и современным методикам обучения [Текст] / А.В. Хуторской  СПб.  2004. -344 с.
   
4. Зайцева Г.Д. Эвристическое обучение математике [Текст] / Г.Д. Зайцева  Бийск: БПГУ им. В.М. Шукшина, 2008. -81 с.
   

ЛЕКЦИЯ №3 (Тезисы)

Методика изучения математических понятий и теорем.

Обучение общим методам решения задач


Термин «понятие» применяется для обозначения мысленного класса объектов реальной действительности и нашего сознания. Класс объектов  объем понятия. Характеристическое свойство  содержание понятия.

Способы введения понятий: конкретно-индуктивный, абстрактно-дедуктивный.

Типовой проект изучения понятия: подготовительный этап; введение нового понятия; конструирование определения; применение нового понятия.

Теорема  это предложение, истинность которого устанавливается путем рассуждений. Виды теорем.

Типовой проект изучения теоремы:

• подготовительный этап;
  
• «открытие» теоремы и ее формулировка;
  
• поиск доказательства теоремы и доказательство;
  
• формирование умений применять теорему.
  

Обучение учащихся решению задач. Этапы решения задачи. Общие методы обучения решению задач: метод проб и ошибок, метод моделирования, метод эвристик, аналитико-синтетический метод, поисково-исследовательский метод.

Типовой проект поисково-исследовательской работы на этапе поиска плана решения задачи: осознание проблемной ситуации, формулировка проблемы, актуализация знаний, формулировка гипотезы, проверка гипотезы, формулировка результата поисковой работы, оценка результата.

Литература:

1. Пойа Д. Как решать задачу [Текст] / Д. Пойа  М.: Учпедгиз, 1959. -207 с.
   
2. Владимирцева, С.А. Теория и методика обучения математике. Общая методика [Текст] / С.А. Владимирцева  Барнаул: Изд-во БПГУ, 2005. -158 с.
   
3. Эсаулов А.Ф. Психология решения задач [Текст] / А.Ф. Эсаулов  М., 1972. -323 с.
   

ЛЕКЦИЯ №4 (Тезисы)

Урок  основная форма обучения


Урок  форма организации обучения учащихся, основными компонентами которого являются: цель, содержание, средства, методы, деятельность по организации и управлению.


Система требований к уроку математики: целенаправленность, соответствие содержания урока поставленной цели, дифференциация процесса обучения, обоснованный выбор средств, методов и приемов обучения, организация продуктивной деятельности учащихся, мотивация учения школьников, сотрудничество учителя и учащихся.

Цели урока: образовательные, развивающие, воспитательные.

Типология уроков: урок изучения новых знаний, урок формирования умений, урок проверки и оценки знаний, комбинированный урок, творческие уроки.

Планирование процесса обучения математике:

• годовое и тематическое планирование;
  
• поурочное планирование, план-конспект урока, требования к плану-конспекту урока.
  

Анализ урока. Схема анализа урока для студентов третьего и четвертого курсов, для студентов пятого курса.

Контроль деятельности учащихся на уроках математики. Функции контроля, принципы контроля, виды контроля. Формы текущего контроля, итогового контроля.

Литература:

1. Методика преподавания математики в средней школе. Общая методика. [Текст] / Р.С. Черкасов, А.А. Столяр  М.: Просвещение, 1986. -336 с.
   
2. Методика преподавания математики в средней школе. Общая методика. Под ред. Ю.М. Колягина [Текст] / Ю.М. Колягин  М.: Просвещение, 1980. -462 с.
   
3. Хуторской А.В. Современная дидактика [Текст] / А.В. Хуторской  СПб.: Питер, 2002. -544 с.
   
4. Зайцева Г.Д. Эвристическое обучение математике [Текст] / Г.Д. Зайцева  Бийск: БПГУ им. В.М. Шукшина, 2008. -81 с.
   

ЛЕКЦИЯ №5 (Тезисы)

Методические особенности изучения числовых множеств

в курсе математики средней школы


Исторические сведения о развитии действительного числа.

Подходы к расширению числовых множеств, рассматриваемые в средней школе:

• вводится новое множество В; затем некоторое его подмножество отождествляется с множеством А;
  
• множество А дополняется новыми числами ; получается расширенное множество .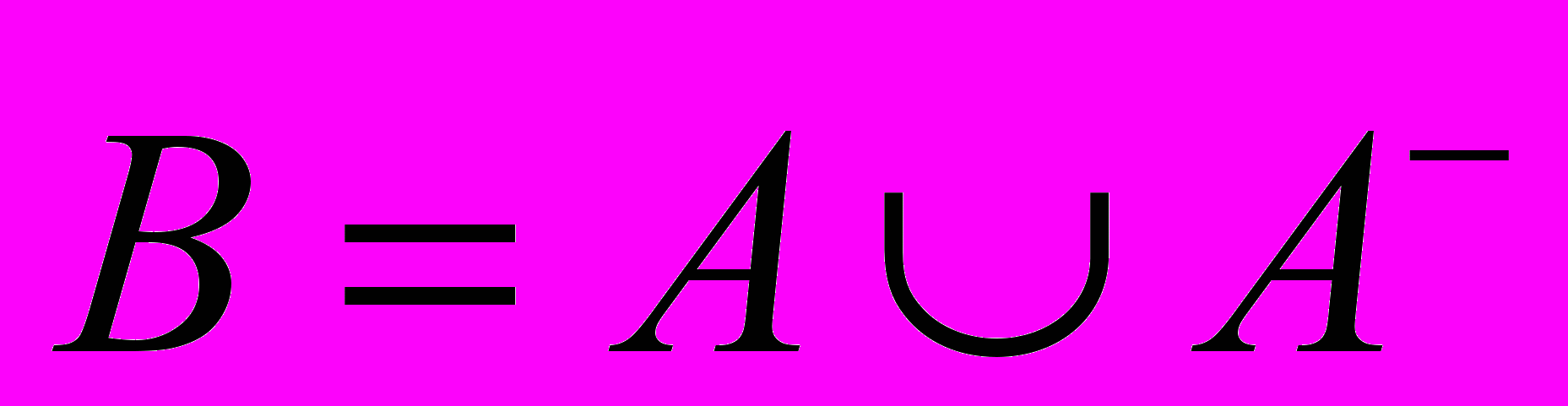
  
• Методические особенности расширения числовых множеств в курсе математики средней школы. Изучение нового числового множества идет по единой схеме:
  
• необходимость новых чисел,
  
• введение новых чисел,
  
• сравнение (геометрическая интерпретация),
  
• действия над числами,
  
• законы действий.
  

Дроби вводятся методом целесообразных задач.

Десятичные дроби могут изучаться раньше, чем обыкновенные. Возможно изучение в обратном направлении.

Каждый способ изучения имеет свои достоинства и недостатки.

Целесообразность введения отрицательных чисел может быть показана учащимся разными способами: через анализ ситуации, в которой действие вычитания не выполнимо, в связи с рассмотрением величин, которые имеют противоположный смысл, на основе графических представлений, как средство изображения расстояний на температурной шкале и др.

К необходимости расширения поля рациональных чисел приводит невозможность в некоторых случаях извлечения корня из положительного числа.

Дальнейшее расширение числовой системы потребовала алгебраическая задача извлечения корня четной степени из отрицательного числа. Возможны и другие подходы.


Литература:

1. Александров П.С. Иррациональные числа [Текст] / П.С. Александров, А.Н. Колмогоров  М.: Учпедгиз, 1961. -213 с.
   
2. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1985. -416 с.
   
3. Методика и технология обучения математике. [Текст] Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №6 (Тезисы)

Методика изучения функций в основной школе


Исторические сведения о развитии понятия «функция».

Цели изучения функции в основной школе.

Различные трактовки понятия «функция», «переменная величина», «закон (правило)», «соответствие», «отношение».

Формирование понятия функции в школьном обучении. Изучение этого понятия имеет несколько уровней:

• пропедевтический уровень (первый этап) имеет место в начальной школе; при изучении разных тем учащимся разъясняется, что такое зависимость между величинами;
  
• пропедевтический уровень (второй этап) отличается от первого содержанием деятельности учащихся, составляются таблицы значений переменных, рассматриваются диаграммы и т.п.;
  
• базовый уровень реализуется в 7 классе; функция рассматривается как связь, закон или как зависимая переменная; формируется общее представление о функции и ее свойствах.
  

В старшей школе реализуется более высокий уровень формирования понятия функции. Учащиеся учатся общему исследованию функции (открытию свойств, их доказательству).

Литература:

1. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1985. -416 с.
   
2. Мордкович А.Г. Новая концепция школьного курса алгебры [Текст] / А.Г. Мордкович  М.: Высшая школа.  1996. - №6. –С.121-132.
   
3. Методика и технология обучения математике. [Текст] Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №7 (Тезисы)

Методика изучения уравнений и неравенств

в курсе алгебры 7-9 классов


Роль уравнений и неравенств в курсе математики. Прикладная направленность, теоретико-математическая направленность, направленность на установление связей с остальным содержанием курса математики.

Основные понятия темы «Уравнения и неравенства»: понятие «уравнение», понятие «равносильность», три основных типа преобразований.

Методические особенности изучения уравнений и неравенств в основной школе:

• решаемые в начальной школе уравнения имеют единственный корень;
  
• решаемые на основе связи между компонентами действий уравнения представляют более сложную структуру;
  
• появляется новый тип уравнений, записанных в виде равенства двух частных;
  
• изучение степени натурального числа позволяет решать уравнения подбором;
  
• знакомство с отрицательными числами позволяет переносить члены уравнения из одной части в другую;
  
• с началом систематического курса алгебры основное внимание уделяется решению линейных и квадратных уравнений и неравенств, которые становятся специальным объектом изучения;
  
• с проблемой понимания равносильности учащиеся встречаются при решении дробно-рациональных уравнений и иррациональных уравнений;
  
• изучение уравнений и неравенств связывается с изучением функций, осуществляется знакомство с методом интервалов;
  
• время, отводимое на изучение уравнений и неравенств, составляет около трети всего времени, отводимого на изучение алгебры в основной школе.
  

Литература:

1. Лященко Е.И. Методика обучения математике в 4-5 классах [Текст] / Е.И. Лященко, А.А. Мазаник – Минск, 1976. -222 с.
   
2. Методика и технология обучения математике. [Текст] Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №8 (Тезисы)

Логическое строение школьного курса геометрии


Ознакомление учащихся с основными идеями современной математики.

Сущность аксиоматического метода построения теории.

Свобода выбора основных понятий и аксиом.

Требования к системе аксиом: непротиворечивость, независимость, полнота.

Реализация идеи логического строения геометрии в школьных учебниках геометрии.

О методике проведения в 9 классе заключительной беседы о логическом строении геометрии:

• показать необходимость выделения основных понятий;
  
• показать необходимость выделения системы аксиом;
  
• рассказать о различных учебниках школьного курса геометрии;
  
• познакомить учащихся с возможностью существования различных геометрий (Евклидовой геометрии, геометрии Лобачевского, геометрии Римана);
  
• на популярном уровне рассмотреть некоторые геометрические предложения и их доказательства геометрии Лобачевского, проиллюстрировать их на псевдосфере.
  

Литература:

1. Атанасян Л.С. и др. Геометрия 7-9 [Текст] /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина  М.: Просвещение, 1991. -207 с.
   
2. Атанасян Л.С. и др. Геометрия 10-11 [Текст] /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк  М.: Просвещение, 2003. -335 с.
   
3. Погорелов А.В. Геометрия 7-11 [Текст] / А.В. Погорелов  М., 2003. -384 с.
   
4. Кутузов Б.В. Геометрия Лобачевского и элементы оснований геометрии [Текст] / Б.В. Кутузов, - М.: Просвещение, 1995. -210 с.
   

ЛЕКЦИЯ №9 (Тезисы)

Изучение геометрических преобразований

на плоскости и в пространстве


Исторические сведения о геометрических преобразованиях на плоскости и в пространстве.

Реализация изучения темы в школьных учебниках геометрии:

• в учебнике А.Н. Колмогорова геометрические преобразования служили средством изучения геометрических объектов;
  
• в ныне действующих учебниках геометрии эта тема является объектом изучения; главная цель разобраться, что такое геометрическое преобразование, в частности, движение;
  
• в учебнике А.В. Погорелова понятие «движение» необходимо для введения общего понятия «равенство фигур»;
  
• движения (преобразования)  завершающая тема в учебниках Л.С. Атанасяна и др. и А.Д. Александрова и др. при изучении курса геометрии они не работают.
  
• Методические рекомендации по изучению геометрических преобразований:
  
• в 5-6 классах имеет смысл научить строить фигуру, симметричную данной относительно точки и прямой;
  
• более глубокое изучение свойств симметричных фигур целесообразно в теме «Четырехугольники»;
  
• при изучении окружности имеет смысл изучить поворот вокруг точки;
  
• свойства параллельного переноса целесообразно рассматривать при изучении векторов;
  
• подобие (основной метод доказательства в геометрии) является центральным вопросом при изучении геометрических преобразований в любом учебнике геометрии и требует тщательного изучения.
  

Литература:

1. Александров А.Д. Геометрия 8-9 [Текст] / А.Д. Александров  М., 1991. -220 с.
   
2. Болтянский В.Г. Преобразования. Векторы [Текст] / В.Г. Болтянский, И.М. Яглом  М., 1964. -303 с.
   
3. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1985. -416 с.
   
4. Методика и технология обучения математике. [Текст] Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №10 (Тезисы)

Изучение векторов и координат на плоскости и в пространстве


Исторические замечания о векторах и координатах.

Основные подходы к изучению векторов и координат в различных учебниках геометрии:

• в учебниках А.Н. Колмогорова вектор вводится как параллельный перенос; координатный метод подробно рассматривался в старшей школе (в учебниках З.А. Скопеца);
  
• в учебниках А.Д. Александрова вводится понятие векторной величины; направленный отрезок является лишь изображением вектора;
  
• в учебниках Л.С. Атанасяна и векторные величины, и направленные отрезки являются векторами;
  
• в учебнике А.В. Погорелова вектором называют направленный отрезок, сразу вводятся координаты вектора, что ведет к алгебраизации данной темы.
  

Методические рекомендации по изучению векторов и координат на плоскости и в пространстве:

• изучение векторов следует согласовать с опытом действий над векторами, который приобрели школьники при изучении физики;
  
• основные понятия могут быть рассмотрены на одном уровне при выполнении специально подобранных заданий с использованием примеров из жизненной практики, физики;
  
• при изучении операций над векторами использовать специально разработанные задания типа: «На тело действуют несколько сил. Какую силу называют равнодействующей? Как вы складываете силы?»;
  
• изучение скалярного произведения векторов и его свойств может быть организовано в виде семинара;
  
• рассмотреть сущность векторного метода решения задач, выделить аффинные задачи и метрические задачи;
  
• рассмотреть использование координатного метода решения геометрических задач, целесообразность введения системы координат, подчеркнуть преимущество векторного и координатного методов перед традиционными при решении определенных задач.
  

Литература:

1. Болтянский В.Г. Преобразования. Векторы [Текст] / В.Г. Болтянский, И.М. Яглом  М., 1964. -303 с.
   
2. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1985. -416 с.
   
3. Методика и технология обучения математике. [Текст] Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №11 (Тезисы)

Методические рекомендации по изучению темы «Площади фигур»


Данную тему целесообразно изучать с применением лекционно-зачетной системы обучения.

На первом уроке проводится школьная лекция-беседа, на которой учащиеся узнают, что такое площадь фигуры, как вычисляются площади различных фигур.

При этом используется таблица-презентация с опорными сигналами.

На втором уроке проводится теоретический зачет.

Начиная с третьего урока по шестой включительно, учащихся обучают решению опорных задач по теме: «Площади фигур». При этом применяют эвристическую беседу, системы рисунков-кадров, лабораторные работы, поисково-исследовательскую деятельность и др.

На седьмом уроке целесообразно провести зачет №2 по решению опорных задач.

На следующих пяти уроках учащихся обучают решению более сложных задач, организуя поисково-исследовательскую деятельность.

Зачет №3 по проверке умений решать более сложные задачи возможно провести в виде контрольной работы при проведении нетрадиционных форм зачетов «Биржа знаний», «Мозговая атака», «Ринг» и др.

Литература:

1. Гусев В.А. Практикум по элементарной математике. Геометрия. [Текст] / В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович  М.: Просвещение, 1992. -352 с.
   
2. Атанасян Л.С. Геометрия 7-9 [Текст] /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина  М.: Просвещение, 2006. -207 с.
   
3. Атанасян Л.С Геометрия 10-11 [Текст] /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Л.С. Киселева, Э.Г. Позняк  М.: Просвещение, 1992. -335 с.
   

ЛЕКЦИЯ №12 (Тезисы)

Методика изучения параллельности и перпендикулярности

на плоскости и в пространстве


В учебниках геометрии параллельность и перпендикулярность на плоскости не выделяется в самостоятельную тему. Материал рассредоточен по различным темам. Такая ситуация снижает набор решаемых задач.

Методические рекомендации к изучению параллельности на плоскости и в пространстве:

• выполнить классификацию взаимного расположения прямых в пространстве и на плоскости;
  
• основным материалом при изучении параллельности прямых являются признаки и свойства параллельных прямых;
  
• на первых уроках стереометрии использовать модели пирамид, параллелепипедов, призм;
  
• целесообразно организовать специально продуманную методику обучения решению задач на доказательство существования (воображаемое построение);
  
• обучать решению позиционных задач на построение на изображениях многогранников.
  

Методические рекомендации к изучению перпендикулярности на плоскости и в пространстве:

• осознать важность изучения темы для определения углов, расстояний, вычисления поверхностей и объемов, для изучения темы «Векторы и координаты в пространстве»;
  
• использовать аналогию при изучении перпендикулярности на плоскости и в пространстве;
  
• особое внимание уделить изучению теорем-признаков, теорем-свойств;
  
• организовать обучение решению задач на доказательство существования (воображаемое построение);
  
• продолжить обучение учащихся решению задач на построение на изображениях многогранников, используя мультимедийные средства.
  

Литература:

1. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1987. -416 с.
   
2. Методика и технология обучения математике. [Текст] Курс лекций./
   

Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.


ЛЕКЦИЯ №13 (Тезисы)

Методические рекомендации по изучению темы «Многогранники»


Данную тему целесообразно изучать лекционно-зачетным методом.

Первые два урока отводятся на изучение теоретического материала в виде лекции-визуализации. На третьем уроке проводится теоретический зачет.

Начиная с четвертого урока по девятый включительно учащихся обучают решению опорных задач по теме «Многогранники». При формировании умений учащихся в решении опорных задач следует применять модели, визуальные материалы с готовыми решениями, изучение решений в сборниках задач и т.п. На десятом уроке проводится зачет №2 по опорным задачам.

На следующих пяти уроках учащихся обучают решению более сложных задач. При этом используется обобщенный прием поисково-исследовательской деятельности, используется совокупность опорных задач. Далее проводится зачет №3. При этом целесообразно использовать нетрадиционные формы проведения зачетов: «Ринг», «Биржа знаний» и др.

Использование лекционно-зачетной системы способствует развитию способностей самостоятельно актуализировать знания и опыт, выделять существенные связи между элементами задачи, переносить знания в новые ситуации, переформулировать задачу, осуществлять мыслительные пробы по ее решению.

Литература:

1. Селевко Г.К. Современные образовательные технологии [Текст] / Г.К. Селевко  М.: Просвещение, 1988. -416 с.
   
2. Эрдниев П.М. Укрупнение дидактических единиц в преподавании математики [Текст] / П.М. Эрдниев  М.: Просвещение, 1977. -321 с.
   
3. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1987. -416 с.
   

ЛЕКЦИЯ №14 (Тезисы)

Методика изучения темы «Тела вращения»


Введение понятий «цилиндр», «конус», «шар» осуществить абстрактно-дедуктивным методом.

При обучении схематическому изображению тел вращения, наблюдая за их изображениями в учебнике, следует выделять обобщенные приемы построения изображений.

Изучение элементов тел вращения предложить учащимся осуществить самостоятельно, проиллюстрировать знания на моделях и рисунках.

После освоения элементов тел вращения целесообразно провести самостоятельное обдумывание вопросов, касающихся свойств тел вращения. Например, почему основания цилиндра равны?

Почему ось цилиндра параллельна образующим?

Изучение теорем о сечениях цилиндра (конуса, шара) плоскостью осуществляется по известному типовому проекту изучения теорем.

При изучении темы «Сфера» по учебнику Л.С. Атанасяна и др. авторов для организации продуктивного обучения целесообразно использовать аналогию.

Перед введением понятия «сфера» на экране поместить определение окружности. Далее предложить учащимся сформулировать определение сферы.

Также с использованием аналогии вводится понятие уравнения, поверхности, выводится уравнение сферы, изучается взаимное расположение сферы и плоскости.

При изучении площадей поверхностей и объемов тел вращения использовать геометрические идеи предельных переходов от поверхностей или объемов многогранников, вписанных в тела вращения, к поверхностям или объемам тел вращения.

Литература:

1. Атанасян Л.С. Геометрия 10-11 [Текст] /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Л.С. Киселева, Э.Г. Позняк  М.: Просвещение, 2003. -335 с.
   
2. Погорелов А.В. Геометрия 7-11 [Текст] / А.В. Погорелов  М., 2003. -384 с.
   
3. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1987. -416 с.
   
4. Методика преподавания математики в средней школе. Частная методика. Под ред. Ю.М. Колягина [Текст] / Ю.М. Колягин  М.: Просвещение, 1977. -461 с.
   

ЛЕКЦИЯ №15 (Тезисы)

Методика изучения объемов в школьном курсе геометрии


Формирование понятия объема простого тела осуществляется с использованием аналогии: вспоминается определение площади простой фигуры и предлагается учащимся сформулировать определение объема простого тела.

При изучении объемов параллелепипеда, призмы, пирамиды, целесообразно организовать продуктивное обучение. На начальном этапе осуществляется мотивация предстоящей учебной деятельности и целеполагание. Затем создается образовательная ситуация, разрешение которой способствует отысканию способа вычисления объема того или иного многогранника. Для разрешения образовательной ситуации учителем создается образовательная среда: системы моделей, визуальных материалов и т.п.

Образовательная среда помогает каждому ученику выбрать свое направление учебной работы. В результате создаются образовательные продукты  способы открытия, доказательства формул вычисления объемов многогранников.

Применение метода вычисления объемов тел, основанного на понятии интеграла, значительно упрощает доказательство теорем об объемах геометрических тел, экономит учебное время, формирует у учащихся единый взгляд на математику. При изучении основной формулы для вычисления объемов тел целесообразно организовать продуктивное обучение, используя аналогию. С учащимися повторяют способ вычисления площади криволинейной трапеции с помощью интеграла (используется таблица-презентация). Старшеклассникам предлагается рассмотреть аналогичную теорему-презентацию для получения общей формулы объема, применить ее для вычисления объемов цилиндра, конуса, шара.

Литература:

1. Атанасян Л.С. Геометрия 10-11 [Текст] /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Л.С. Киселева, Э.Г. Позняк  М.: Просвещение, 2003. -335 с.
   
2. Погорелов А.В. Геометрия 7-11 [Текст] / А.В. Погорелов  М., 2003. -384 с.
   
3. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1987. -416 с.
   
4. Зайцева Г.Д. Эвристическое обучение математике [Текст] / Г.Д. Зайцева  Бийск: БПГУ им. В.М. Шукшина, 2008. -81 с.
   

ЛЕКЦИЯ №16 (Тезисы)


Методика изучения тригонометрических функций


На современном этапе учебный материал по тригонометрии изучается небольшими порциями в курсе геометрии 8, 9 классов, а затем в курсе алгебры и начал анализа в 10-11 классах. Это связано с постепенным расширением понятий угла и дуги и связанных с ними определениями тригонометрических функций.

Систематическое изучение тригонометрических функций числового аргумента осуществляется в 10 классе. На подготовительном этапе целесообразно освоить с учащимися общие знания о функции: ее свойствах и графике.

При изучении каждой из тригонометрических функций целесообразно организовать продуктивное обучение через создание и разрешение образовательных ситуаций (мотивация, проблематизация, создание продуктов образовательной деятельности, демонстрация продуктов и их сравнение, рефлексия).

При создании образовательной среды учитель дает направление поисковой деятельности учащихся: а) построить график тригонометрической функции по точкам и сформулировать ее свойства; б) исследовать формулу, задающую тригонометрическую функцию, и по результатам исследования построить график.


Литература:

1. Мордкович А.Г. Алгебра и начала анализа 10-11 класс [Текст] / А.Г. Мордкович  М.: Мнемозина, 2003. -373 с.
   
2. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1987. -416 с.
   
3. Алгебра и начала анализа 10-11. Под ред. А.Н. Колмогорова [Текст] / А.Н. Колмогоров  М.: Просвещение, 2005. -384 с.
   
4. Зайцева Г.Д. Эвристическое обучение математике [Текст] / Г.Д. Зайцева  Бийск: БПГУ им. В.М. Шукшина, 2008. -81 с.
   

ЛЕКЦИЯ №17 (Тезисы)


Изучение элементов математического анализа

в курсе алгебры средней школы


Основные линии курса алгебры и начал анализа: линия числа, линия функций, линия тождественных преобразований, линия элементов анализа.

Общие закономерности изложения учебного материала:

• более высокий уровень абстракции и логической организации изучаемого материала;
  
• переход изучения на уровень методов (методы дифференциального исчисления, векторный и координатный методы);
  
• знакомство с фундаментальными понятиями математики (производная функции, определенный интеграл, предел функции);
  
• систематизируются и обобщаются знания школьников;
  
• усиливается прикладная направленность школьного курса математики.
  

Предел функции, как и предел последовательности, являются фундаментальными понятиями математики. Можно использовать конкретно-индуктивный подход к введению этих понятий. При этом можно сформулировать окрестное определение предела последовательности и окрестное определение предела функции в точке.

На основе имеющихся знаний о пределе функции в точке может быть сформулировано определение производной. При этом целесообразно воспользоваться как геометрической иллюстрацией, так и обратиться к физическим закономерностям.

При обучении исследованию функций с помощью производной: изучение теорем следует осуществлять с использованием типового проекта изучения теорем; использовать схему исследования функции.

Изучение интеграла целесообразно начать с беседы с учащимися о том, что у операции дифференцирования функций существует обратная операция, называемая интегрированием. На этой логической основе, используя таблицу производных, построить таблицу функций, производные которых равны заданным и ввести определение первообразной функции.

Литература:

1. Мордкович А.Г. Алгебра и начала анализа 10-11 класс [Текст] / А.Г. Мордкович  М.: Мнемозина, 2003. -373 с.
   
2. Виленкин Н.Я. Производная и интеграл. [Текст] / Н.Я. Виленкин, А.Г. Мордкович  М.: Прсвещение, 1976. -163 с.
   
3. Методика и технология обучения математике. [Текст] Курс лекций./
   
4. Н.Л. Стефанова, Н.С. Подходова  М.: Дрофа, 2005. -416 c.
   

ЛЕКЦИЯ №18 (Тезисы)

Методика изучения степенной, показательной и логарифмической функций в средней школе


Методика изучения показательной функции аналогична методике изучения функций в основной школе: построение графика по точкам, формулирование свойств. Этому способствует содержание школьных учебников.

Непосредственно перед изучением логарифмической функции целесообразно ознакомить учащихся с понятием «обратная функция»; выделить обобщенный прием алгоритмического типа нахождения обратной функции; на конкретных примерах ознакомить учащихся со свойствами графиков функции и ей обратной функции.

На начальном этапе изучения логарифмической функции следует повторить определение логарифма, повторить обобщенный прием нахождения обратной функции, выяснить, показательная функция может ли иметь обратную.

В совместной учебной работе, используя обобщенный прием отыскания обратной функции, находят функцию обратную показательной, которая имеет вид 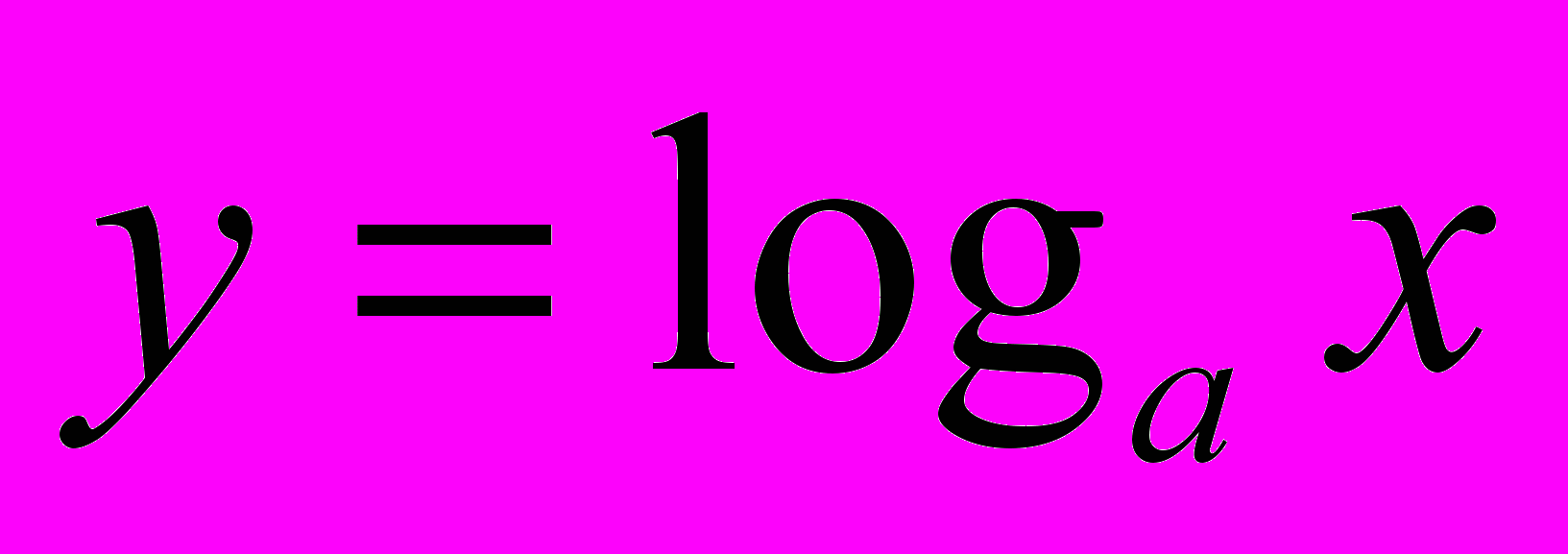, где .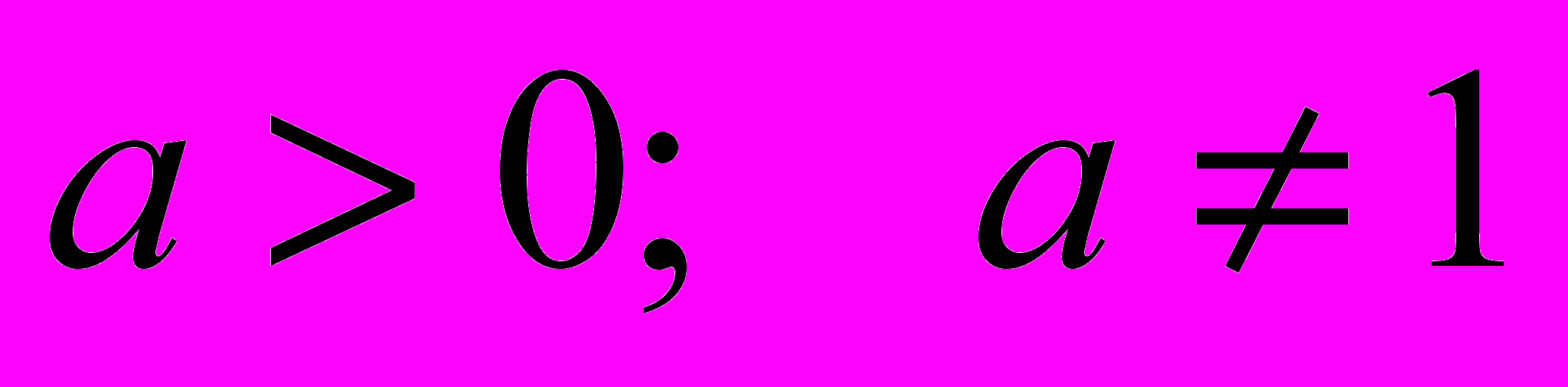

График логарифмической функции строится на основе свойств графиков взаимно обратных функций. Далее осуществляется формулирование свойств логарифмической функции.

Возможен и другой подход к изучению логарифмической функции соответствующий порядку изложения учебного материала в школьных учебниках.

В старшей школе происходит обобщение знаний о степенной функции, которые учащиеся получили в основной школе. Этому способствует возможность исследования степенной функции с помощью производной.

Литература:

1. Мордкович А.Г. Алгебра и начала анализа 10-11 класс [Текст] / А.Г. Мордкович  М.: Мнемозина, 2003. -373 с.
   
2. Методика преподавания математики в средней школе. Частные методики. Состав. В.И. Мишин [Текст] / В.И. Мишин.  М.: Просвещение, 1987. -416 с.
   
3. Алгебра и начала анализа 10-11. Под ред. А.Н. Колмогорова [Текст] / А.Н. Колмогоров  М.: Просвещение, 2005. -384 с.
   
4. Зайцева Г.Д. Эвристическое обучение математике [Текст] / Г.Д. Зайцева  Бийск: БПГУ им. В.М. Шукшина, 2008. -81 с.
   

3.2. Методические рекомендации по проведению семинарских занятий

по курсу ТиМОМ

§1. Семинарское занятие № 1