Методические рекомендации для студентов по изучению дисциплины 29 1

Вид материала

Содержание

Самостоятельная работа студентов
Оборудование и средства обучения
II. Мотивационный этап.
IV. Формулировка теоремы. Работа над формулировкой.
VI. Формирование умений применять теорему.
Цель лабораторной работы
Оборудование и средства обучения
Самостоятельная работа студентов
Цель лабораторной работы
Оборудование и средства обучения
Самостоятельная работа студентов
Цель лабораторной работы
Оборудование и средства обучения

Подобный материал:

1 2 3 4 5 6 7 8

§1. Лабораторная работа № 1

Методика формирования математических понятий
у учащихся средней школы

Цель лабораторной работы: продолжить развитие умений и навыков студентов в разработке эвристических технологий освоения математических понятий у учащихся средней школы.

Оборудование и средства обучения:

1. Учебники:

Погорелов, А.В. . Геометрия 7-11 [Текст] / А.В. Погорелов – М.: Просвещение, 1991. -384 с.
Атанасян, Л.С. Геометрия 7-9 [Текст] / Л.С. Атанасян и др. – М.: Просвещение 1991. -335 с.
Мордкович, А.Г. Алгебра 7 [Текст] / А.Г. Мордкович – М.: Мнемозина, 2002. -160 с.
Макарычев, Ю.Н. Алгебра 7 [Текст] / Под ред. С.А. Теляковского / Ю.Н. Макарычев и др. – М.: Просвещение 1985. -223 с.
Алгебра 10-11 [Текст] / Под ред. А.Н. Колмогорова. – М.: Просвещение, 1991. -320 с.
Зайцева, Г.Д. Содержание и методика проведения лабораторных занятий по теории и методике обучения математике [Текст] : методические рекомендации для студентов педвуза. / Г.Д. Зайцева, А.М. Старикова. – Бийск: РИО БПГУ им. В.М. Шукшина, 2009. -69 с.

2. Таблица «Основные этапы изучения математических понятий в школе».

3. Модели правильных многогранников.

4. Компьютерные средства обучения (презентации с компьютерным моделированием в программах Excel и Word).

5. Задания для выполнения контрольных этапов формирования понятий.

6. Список дополнительной литературы.

Основное содержание лабораторной работы:

Задание №1. Систематизировать знания о понятиях и их определениях, ответив на вопросы:

1. Что такое объект и понятие об объекте?

2. Существенные и несущественные свойства понятия.

3. Содержание и объем понятия.

4. Логическое действие: «определение понятия».

5. Виды определений математических объектов.

Задание №2. Повторите методическую схему конкретно – индуктивного метода формирования математического понятия.

1. Мотивация изучения нового понятия.

2. Рассмотрение конкретных примеров объектов, входящих в объем вводимого понятия.

(Происходит наблюдение, сравнивание внешних свойств предметов, появляются эмпирические знания. Осуществляется осознание, осмысление понятия на начальном уровне, начинается создание представления о вводимом понятии).

3. Фиксирование внимания учащихся на характеристических свойствах (определяющих признаках) вводимого понятия.

(Происходит абстрагирование, освобождение от несущественных признаков, выделение общих существенных свойств, основных закономерностей, которые не всегда заметны сразу; появляются теоретические знания и неразрывно связанное с ним теоретическое мышление).

4. Введение термина (название вводимого понятия).

5. Формулирование определения учениками.

(Реализуется принцип первичности образовательной продукции учащихся).

6. Формулировка определения учителем (или чтение по книге).

7. Закрепление:

а) повторение формулировки определения,

б) повторение характеристических существенных свойств,

в) узнавание объектов, входящих в объем данного понятия.

Задание №3. Изучите методические рекомендации по использованию схемы конкретно – индуктивного метода при освоении понятия «правильный многоугольник».

Задание №4. Вспомните методическую схему абстрактно–дедуктивного метода формирования математического понятия:

1. Сформулировать определение понятия.

2. Рассмотреть примеры объектов, входящих в объем, определяемого понятия.

3. Зафиксировать внимание учащихся на существенных признаках понятия.

Выполнить упражнения на усвоение введенного понятия.

Задание №5. Разработайте методические рекомендации по формированию понятия «криволинейная трапеция» абстрактно-дедуктивным методом.

Самостоятельная работа студентов:

Задание №6. Раскройте основные этапы формирования понятия конкретно-индуктивным и абстрактно-дедуктивным методами. Каждый студент письменно выполняет индивидуальное задание (один из вариантов):

1. Угол.

2. Процент.

3. Среднее арифметическое.

4. Вертикальные углы.

5. Смежные углы.

6. Функция.

7. Вписанный угол.

8. Правильный многогранник.

9. Пирамида.

10. Призма.

11. Косинус угла.

12. Арксинус числа а.

13. Четная функция.

14. Тождество.

15. Трапеция.

Аккуратно оформленная работа сдается на проверку преподавателю.

Дополнительная литература:

Методика преподавания математики. Общая методика [Текст] / Сост. Р.С. Черкасов, А.А. Столяр – М.: Просвещение, 1986. -336 с.
Лабораторные и практические занятия по методике преподавания математики. [Текст] / Сост. Е.И. Лященко. – Ленинград, 1988. -88 с.
Владимирцева, С.А. Теория и методика обучения математике. Общая методика [Текст] / С.А. Владимирцева – Барнаул: БПГУ, 2005. -158 с.
Зайцева, Г.Д. Использование современных дидактических концепций при обучении учащихся на уроках математики в средней школе [Текст] / Г.Д. Зайцева – Бийск: БПГУ им. В.М. Шукшина, 2004. -89 с.
Зайцева, Г.Д. Эвристическое обучение математике [Текст] / Г.Д. Зайцева – Бийск: БПГУ им. В.М. Шукшина, 2008. -81 с.

§2. Лабораторная работа № 2

Методика изучения теорем и их доказательств

Цель лабораторной работы: продолжить развитие умений и навыков студентов в разработке эвристических технологий освоения теорем и их доказательств.

Оборудование и средства обучения:

1. Учебники:

Погорелов, А.В. Геометрия 7-11 [Текст] / А.В. Погорелов.  Просвещение, 1991.

-384 с.

Атанасян, Л.С. Геометрия 7-9 [Текст] / Л.С. Атанасян и др. – М.: Просвещение, 1991. -335 с.

Атанасян, Л.С. Геометрия 10-11 [Текст] / Л.С. Атанасян и др. – М.: Просвещение, 1991. -207 с.

Алгебра 10-11 [Текст] / Под ред. А.Н. Колмогорова – М.: Просвещение, 1991. -320 с.

Зайцева, Г.Д. Содержание и методика проведения лабораторных занятий по теории и методике обучения математике [Текст] : методические рекомендации для студентов педвуза. / Г.Д. Зайцева, А.М. Старикова. – Бийск: РИО БПГУ им. В.М. Шукшина, 2009. -69 с.

2. Таблица «Основные этапы изучения теоремы».

3. Таблицы с рисунками геометрических фигур, модели геометрических фигур, способствующие организации и проведению мотивационного этапа изучения теоремы «о сумме углов треугольника», открытию, формулированию теоремы, эвристической беседы по доказательству теоремы, формирования умения применять теорему.

4. Компьютерные средства обучения (презентации с компьютерным моделированием в программах Excel и Word).

5. Задания для выполнения лабораторной работы.

6. Список дополнительной литературы.

Основное содержание лабораторной работы:

Задание №1. Систематизировать знание о теоремах, ответив на вопросы:

1. Что такое теорема? Перечислите основные виды теорем.

2. Сущность диалога аналитико-синтетического характера по поиску доказательства теоремы.

3. Доказательство и его структура.

4. Анализ теоремы и ее доказательства.

Задание №2. Повторите методическую схему изучения теоремы и ее доказательства.

I. Подготовительная работа.

Актуализация знаний необходимых для изучения теоремы.

II. Мотивационный этап.

Показывается и осознается необходимость изучения теоремы.

III. Открытие теоремы.

В ходе практической работы, наблюдений, сравнений моделей, рисунков осуществляется эмпирическое мышление, «открытие» математического факта.

IV. Формулировка теоремы. Работа над формулировкой.

V. Доказательство теоремы.

Применение эвристического метода обучения, решение определенной системы задач-проблем с выделением основных этапов доказательства, выявление внутренних закономерностей доказательства.

VI. Формирование умений применять теорему.

Повторение формулировки теоремы, ее основных этапов доказательства, формирование умственного действия «видеть модель теоремы» при решении задач.

Задание №3. Изучите методические рекомендации по использованию выделенной методической схемы при изучении теоремы о сумме углов треугольника.

Задание №4. Изучите методические рекомендации по использованию выделенной методической схемы при изучении теоремы Пифагора.

Задание №5. Разработайте методические рекомендации по организации и проведению мотивационного этапа при изучении теоремы о первом признаке равенства треугольников.

Задание №6. Разработайте методические рекомендации по осуществлению «открытия» теоремы о признаке возрастания функции.

Самостоятельная работа студентов:

Задание №7. Раскройте основные этапы изучения теоремы. Каждый студент письменно выполняет индивидуальное задание (один из вариантов):

1. Теорема о внешнем угле треугольника.

2. Теорема о центре окружности, описанной около треугольника.

3. Теорема о центре окружности, вписанной в треугольник.

4. Теорема о трех перпендикулярах.

5. Теорема о третьем признаке равенства треугольников.

6. Теорема о втором признаке равенства треугольников.

7. Теорема о первом признаке подобия треугольников.

8. Теорема о сумме углов выпуклого многоугольника.

9. Теорема о признаке перпендикулярности прямой и плоскости.

10. Теорема о средней линии трапеции.

11. Теорема о признаке перпендикулярности плоскостей.

12. Теорема о первом признаке параллелограмма.

13. Теорема о втором признаке подобия треугольников.

14. Теорема о признаке параллельности плоскостей.

15. Теорема о признаке параллельности прямых в пространстве.

Аккуратно оформленная работа сдается на проверку преподавателю.

Дополнительная литература:

Методика преподавания математики. Общая методика [Текст] / Сост. Р.С. Черкасов, А.А. Столяр – М.: Просвещение, 1986. -336 с.
Владимирцева, С.А. Теория и методика обучения математике. Общая методика [Текст] / С.А. Владимирцева – Барнаул: БПГУ, 2005. -158 с.
Мостовой, А.И. Различные способы доказательств в курсе геометрии [Текст] /А.И. Мостовой – М.: Просвещение, 2001. -127 с.
Методика изучения теорем в курсе математики средней школы [Текст] / Сост. Г.Д. Зайцева, И.Г. Корнева, Е.В. Храпова  Бийск: НИЦ БиГПИ, 1997. -13 с.
Зайцева, Г.Д. Использование современных дидактических концепций при обучении учащихся на уроках математики в средней школе [Текст] / Г.Д. Зайцева – Бийск: БПГУ им. В.М. Шукшина, 2004. -89 с.

§3. Лабораторная работа № 3

Методика формирования умственных действий
у учащихся при обучении математике

Цель лабораторной работы: продолжить развитие у студентов умений и навыков творческой деятельности по использованию сочетания современных педагогических теорий обучения при формировании умственных действий учащихся при обучении математике.

Оборудование и средства обучения:

1. Учебники школьного курса математики:

Виленкин, Н.Я. Математика 6 [Текст] / Н.Я. Виленкин – М.: Мнемозина, 2005. -288 с.

Зубарева, И.И. Математика 6 [Текст] / И.И. Зубарева, А.Г. Мордкович – М.: Мнемозина, 2005. -245 с.

Макарычев, Ю.Н. Алгебра 7. [Текст] / Под ред. С.А. Теляковского / Ю.Н. Макарычев и др. – М.: Просвещение, 1985. -223 с.

Алгебра и начала анализа 10-11. [Текст] / Под ред. А.Н. Колмогорова. – М.: Просвещение, 1991. -320 с.

Атанасян, Л.С. Геометрия 7-9 [Текст] / Л.С. Атанасян и др. – М.: Просвещение, 1991. -335 с.

Зайцева, Г.Д. Содержание и методика проведения лабораторных занятий по теории и методике обучения математике [Текст] : методические рекомендации для студентов педвуза. / Г.Д. Зайцева, А.М. Старикова. – Бийск: РИО БПГУ им. В.М. Шукшина, 2009. -69 с.

2. Таблицы, наглядные пособия, иллюстрирующие методику поэтапного формирования умственных действий.

3. Компьютерные презентации, уточняющие методические рекомендации по формированию умственных действий учащихся.

4. Задания по выполнению лабораторной работы.

5. Список дополнительной литературы.

Основное содержание лабораторной работы:

Задание №1. Повторите основные положения современных педагогических теорий обучения:

− ассоциативной теории обучения;

− теории о поэтапном формировании умственных действий (П.Я. Гальперин и Н.Ф. Талызина);

− теории о проблемном обучении (А.М. Матюшкин, М.И. Махмутов);

− теории учебной деятельности (В.В. Давыдов, Д.Б. Эльконин);

− мыследеятельностной теории обучения (Г.П. Щедровицкий).

Задание №2. Выделите операционный состав обобщенного приема поэтапного формирования умственных действий, используя сочетание основных идей современных теорий обучения:

1. Мотивация изучения умственного действия (создание проблемной ситуации), «открытие» действия.

2. Выполнение учащимися действия во внешней материализованной форме. Конструирование операционного состава действия (умственного образа действия).

3. Выполнение действия с проговариванием вслух.

4. Выполнение действия в форме проговаривания про себя.

5. Выполнение действия в максимально свернутой форме. Использование действия в новых связях и отношениях.

Задание №3. Изучите конкретный пример использования выделенного операционного состава обобщенного приема поэтапного формирования умственного действия с учащимися шестого класса.

Задание №4. Самостоятельно разработайте методические рекомендации по формированию у учащихся умственного действия «умножение десятичных дробей» с использованием выделенного обобщенного приема.

Задание №5. Проведите фрагмент «урока» в своей подгруппе по освоению правила умножения десятичных дробей. Осуществите рефлексивную деятельность по организации и проведению фрагмента «урока».

Самостоятельная работа студентов:

Задание №6. Выполните индивидуальное домашнее задание по конструированию методических рекомендаций, используемых при формировании умственных действий у учащихся:

1. Сложение десятичных дробей.

2. Деление на десятичную дробь.

3. Формула сокращенного умножения

.

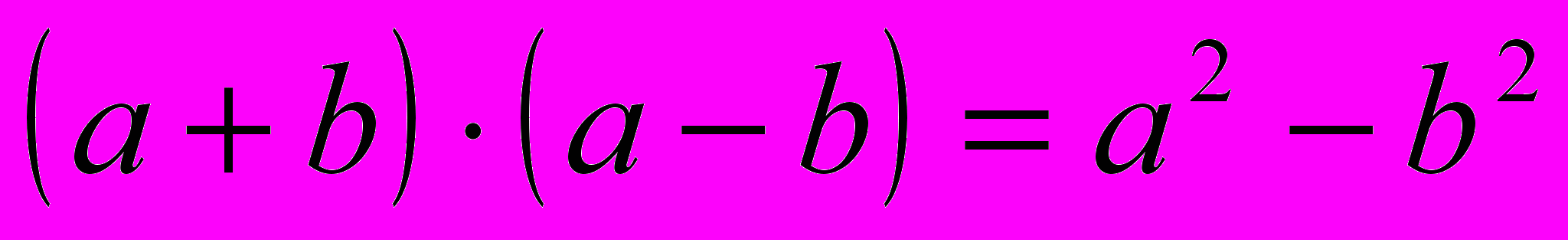4. Построение круговых диаграмм.

5. Умножение чисел с разными знаками.

6. Решение неравенства

.

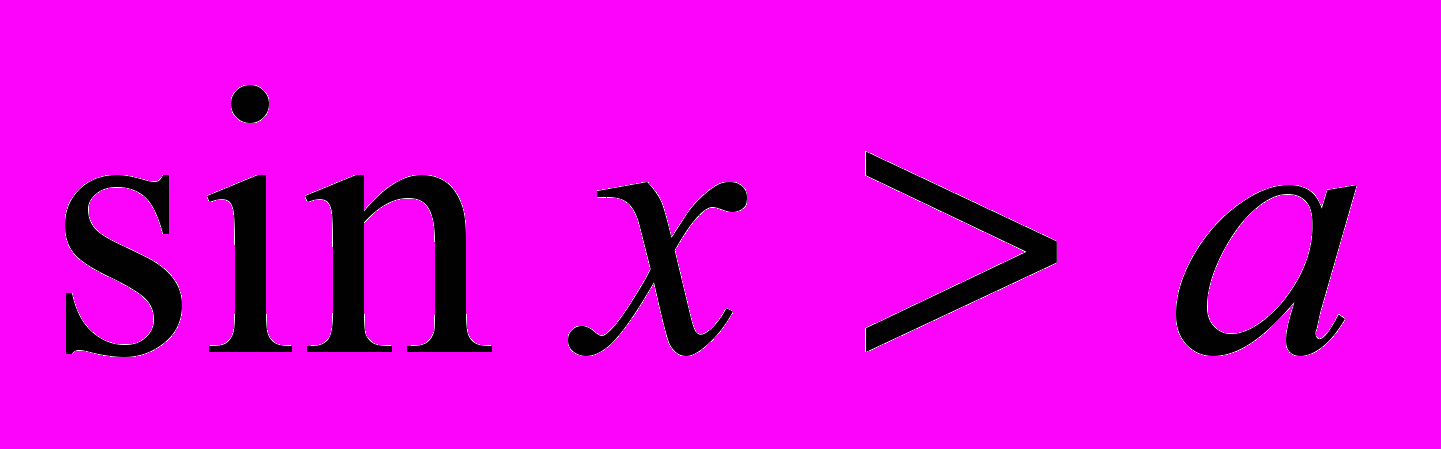7. Построение биссектрисы угла.

8. Деление отрезка пополам.

9. Умножение двух отрицательных чисел.

10. Сокращение дроби.

11. Нахождение среднего арифметического.

12. Деление обыкновенных дробей.

13. Сравнение обыкновенных дробей.

14. Построение центра окружности, описанной около треугольника.

15. Построение центра окружности, вписанной в треугольник.

16. Нахождение нескольких процентов числа.

Аккуратно оформленная работа сдается на проверку преподавателю.

Дополнительная литература:

Педагогика. Педагогические теории, системы и технологии [Текст] / Под ред. С.А. Смирнова. – М.: Академия, 2001. -512 с.
Гальперин, П.Я. Психология мышления и учение о поэтапном формировании умственных действий. [Текст] // Хрестоматия по психологии. Под ред. А.В. Петровского. – М.: Просвещение, 1977. –С. 417-425.
Владимирцева, С.А. Теория и методика обучения математике. Общая методика [Текст] / С.А. Владимирцева. – Барнаул: БПГУ, 2005.- 158 с.

§4. Лабораторная работа № 4

Организация поисково-исследовательской деятельности учащихся средней школы при изучении математики

Цель лабораторной работы: оказать помощь студентам в приобретении начального опыта по организации поисково-исследовательской деятельности учащихся при изучении математики.

Оборудование и средства обучения:

1. Учебники:

Погорелов, А.В. Геометрия 7-11 [Текст] / А.В. Погорелов.  М.: Просвещение, 1991.

-384 с.

Колмогоров, А.Н. Алгебра и начала анализа [Текст] /  М.: Просвещение, 1991. -320 с.

Атанасян, Л.С. и др. Геометрия 10-11. – М. Просвещение 1991. -207 с.

Методика преподавания математики в средней школе. Общая методика [Текст] / Сост. Р.С.Черкасов, А.А.Столяр.  М: Просвещение, 1985. -336 с.

Зайцева, Г.Д. Содержание и методика проведения лабораторных занятий по теории и методике обучения математике [Текст] : методические рекомендации для студентов педвуза. / Г.Д. Зайцева, А.М. Старикова. – Бийск: РИО БПГУ им. В.М. Шукшина, 2009. -69 с.

2. Модели комбинаций многоугольников и сфер.

3. Таблица: «Основные этапы поисково-исследовательской деятельности».

4. «Блокнотик-задание» по отысканию решений простейших тригонометрических неравенств.

5. Методические рекомендации по организации нормотворчества учащихся (конструирования учениками операционного состава обобщенного приема поисково-исследовательской деятельности).

6. Задания для выполнения лабораторной работы.

7. Список дополнительной литературы.

Основное содержание лабораторной работы:

Задание №1. Раскройте сущность проблемного обучения. Сформулируйте основные методы проблемного обучения (проблемное изложение, эвристический метод, исследовательский метод). Объясните различие этих методов.

Задание №2. Выделите основные этапы поисково-исследовательской деятельности; объясните необходимость осуществления каждого этапа.

Задание №3. Изучите готовые рассуждения при отыскании плана решения задачи с использованием основных этапов поисково-исследовательской деятельности.

Задание №4. Разработайте методические рекомендации в форме «блокнотика-задания» по осуществлению поисково-исследовательской деятельности при изучении доказательства теоремы о признаке перпендикулярности плоскостей.

Самостоятельная работа студентов:

Задание №5. Разработайте методические рекомендации по организации поисково-исследовательской деятельности при:

1) формировании математического понятия;

2) изучении теоремы;

3) решении геометрической задачи;

4) конструировании обобщенного приема алгоритмического или эвристического типа.

При выполнении задания №5 выбор математического понятия, теоремы, задачи, обобщенного приема осуществляется по желанию студентов.

Методические рекомендации оформляются письменно и сдаются на проверку преподавателю.

Дополнительная литература:

Владимирцева, С.А. Теория и методика обучения математике. Общая методика [Текст] / С.А. Владимирцева. – Барнаул: БПГУ, 2005. -158 с.
Зайцева, Г.Д. Использование методики развивающего обучения на факультативных занятиях по решению геометрических задач [Текст] / Г.Д. Зайцева. – Бийск: БПГИ, 2002. -114 с.
Зайцева, Г.Д. Использование современных дидактических концепций при обучении учащихся на уроках математики в средней школе [Текст] / Г.Д. Зайцева. – Бийск: БПГУ им. В.М. Шукшина, 2004. -89 с.

§5. Лабораторная работа № 5

Методика обучения решению математических (арифметических, алгебраических, геометрических) задач

Цель лабораторной работы:

ознакомить студентов:

а) с методикой организации сотрудничества между учителем и учащимся при обучении решению задач;

б) с формами оформления решения задачи на доске и в тетрадях.

Оборудование и средства обучения:

1. Учебники:

Виленкин, Н.Я. Математика 5 [Текст] / Н.Я. Виленкин и др. – М.: Мнемозина, 2005.

-280 с.

Виленкин, Н.Я. Математика 6 [Текст] / Н.Я. Виленкин и др. – М.: Мнемозина, 2005.

-288 с.

Зубарева, И.И. Математика 5 [Текст] / И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2005. -270 с.

Зубарева, И.И. Математика 6 [Текст] / И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2005. -245 с.

Макарычев, Ю.Н. Алгебра 7 [Текст] / Ю.Н. Макарычев и др. Под ред. С.А. Теляковского. – М.: Просвещение 1985. -223 с.

Погорелов, А.В. Геометрия 7-11 [Текст] / А.В. Погорелов.  М.: Просвещение, 2003.

-384 с.

Атанасян, Л.С. и др. Геометрия 10-11 [Текст] / Л.С. Атанасян и др. – М.: Просвещение, 1991. -207 с.

Зайцева, Г.Д. Содержание и методика проведения лабораторных занятий по теории и методике обучения математике [Текст] : методические рекомендации для студентов педвуза. / Г.Д. Зайцева, А.М. Старикова. – Бийск: РИО БПГУ им. В.М. Шукшина, 2009. -69 с.

2. Методические рекомендации по обучению решению арифметических, алгебраических, геометрических задач.

3. Задания для выполнения лабораторной работы.

4. Список дополнительной литературы.

Основное содержание лабораторной работы:

Задание №1. Проанализируйте методическую литературу по проблемам обучения решению математических задач (Пойа Д, Колягин Ю.М, Фридман Л.М, Лященко Е.И, Канин Е.С, Нагибин Ф.Ф, Эсаулов А.Ф. и др.). Раскройте сущность учебной работы учащихся на каждом из четырех этапов решения задачи.

Задание №2. Изучите методические рекомендации по обучению учащихся решению арифметических задач.

Решение каждой математической задачи чаще всего осуществляется по четырем основным этапам:

1. Подготовительная работа. Изучение условия и требования задачи.

2. Составление плана решения задачи.

3. Реализация плана решения.

4. Изучение полученного решения.

5. Рассмотрим пример возможной учебной работы при обучении учащихся решению арифметических задач.

Задание №3. Изучите методические рекомендации по обучению учащихся решению алгебраических задач.

Работа над изучением условия алгебраической задачи, работа на заключительном этапе проводится так же, как при обучении решению арифметической задачи.

На втором этапе составления плана решения, применяются следующие приемы:

− постепенная символическая запись условия (5-6 кл.);

− выделение основных соотношений (7-9 кл.).

Задание №4. Вспомните методическую схему обучения решению задач поисково-исследовательским методом. Выполните методический разбор решения геометрической задачи.

Задание №5. Разработайте методические рекомендации по обучению решению:

а) арифметической задачи;

б) алгебраической задачи;

в) геометрической задачи на вычисление или доказательство.

Выбор задач осуществляется по желанию студента из учебников школьного курса математики. Методические разработки оформляются письменно и сдаются на проверку преподавателю.

Дополнительная литература:

Пойа, Д. Как решать задачу [Текст] / Д. Пойа. – М.: Учпедгиз, 1959. -207 с.
Пойа, Д. Математическое открытие [Текст] / Д. Пойа. – М.: Наука, 1970. -453 с.
Эсаулов, А.Ф. Психология решения задач [Текст] / А.Ф. Эсаулов. – М.: Высшая школа, 1972. -235 с.
Колягин, Ю.М. Задачи в обучении математике [Текст] / Ю.М. Колягин.  М.: Просвещение, 1977. -227 с.
Канин, Е.С. Заключительный этап решения учебных задач [Текст] / Канин Е.С. Нагибин Ф.Ф. – М.: Просвещение, 1982. -117 с.

Blog

Методические рекомендации для студентов по изучению дисциплины 29 1

Содержание