Конспект лекций по курсу «финансовый менеджмент»

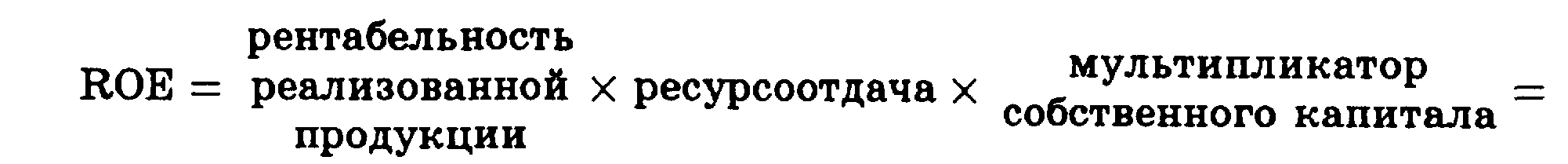
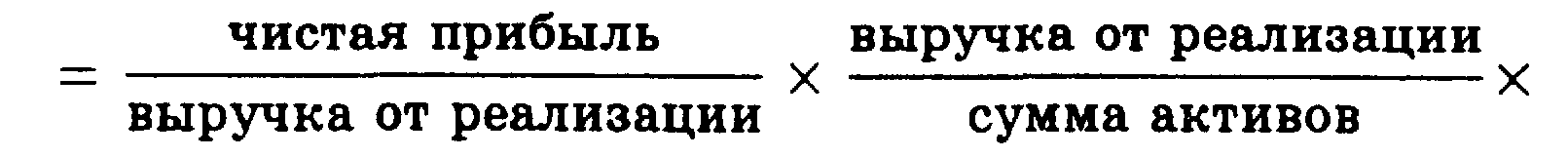
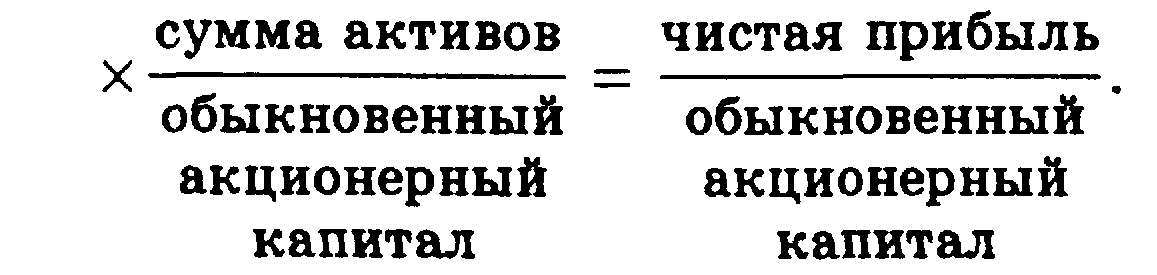
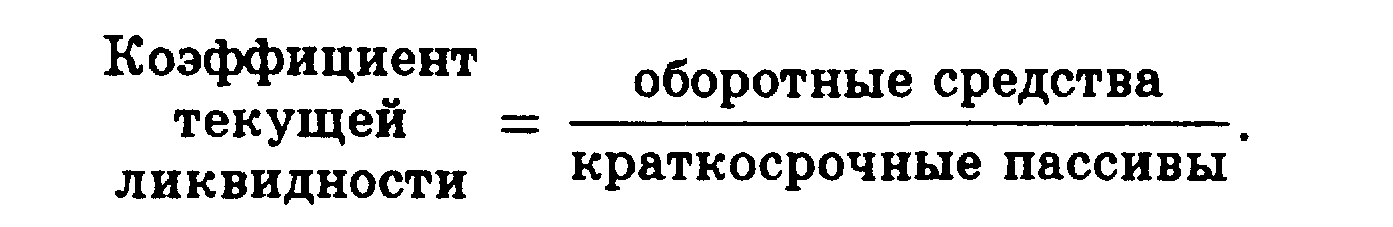
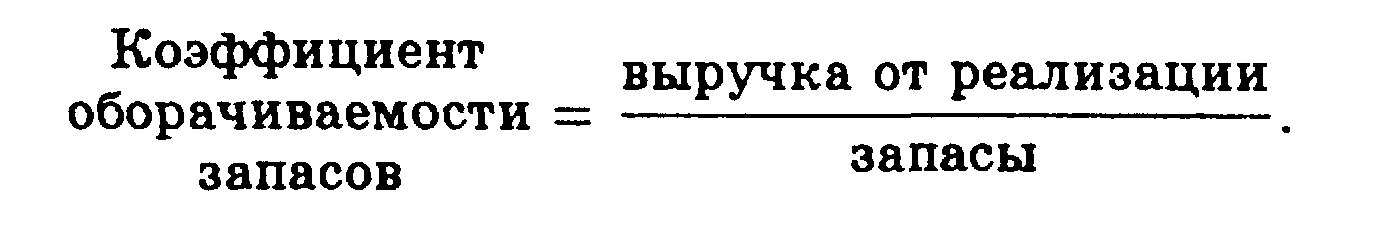
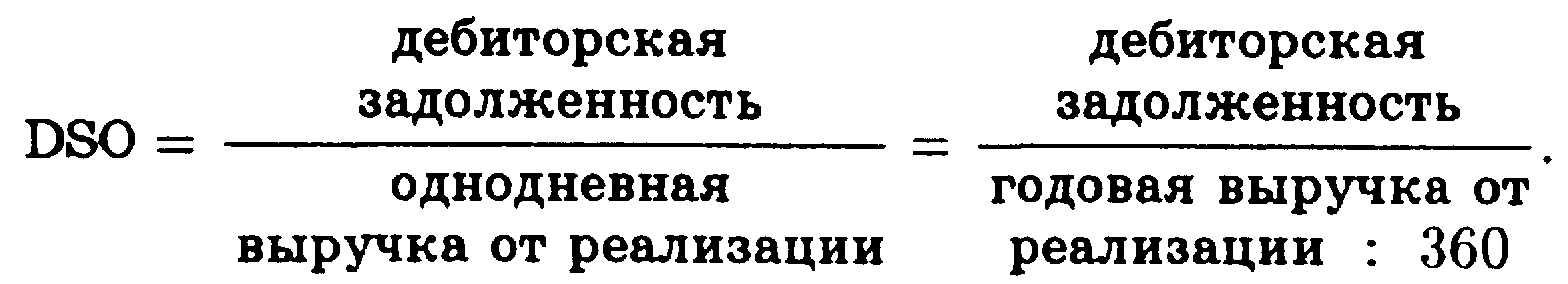
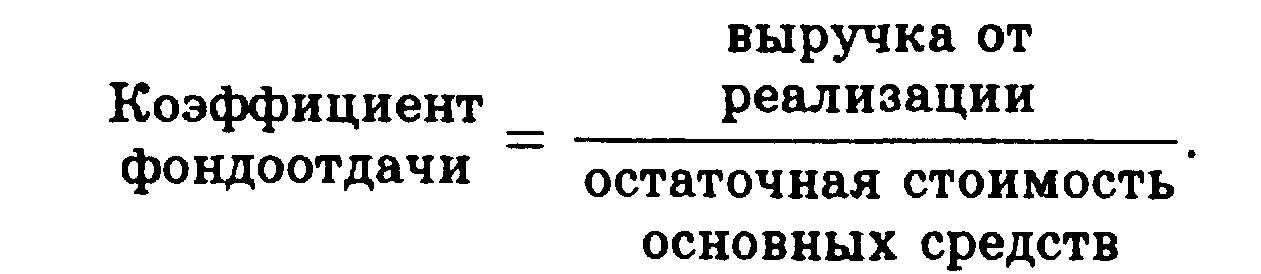
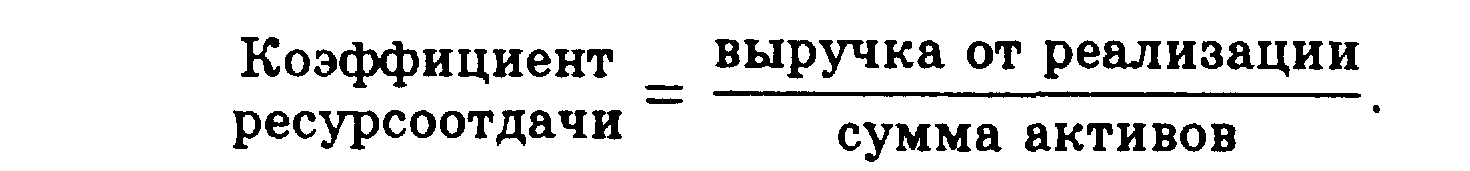
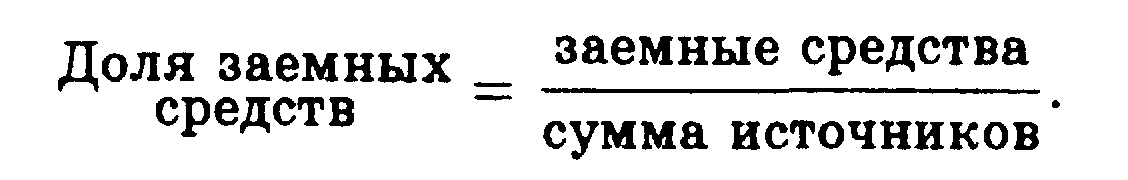
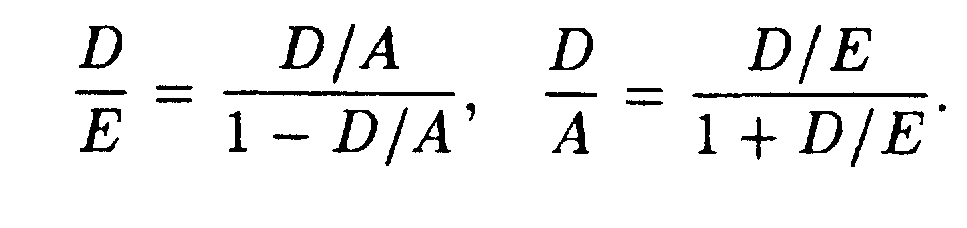
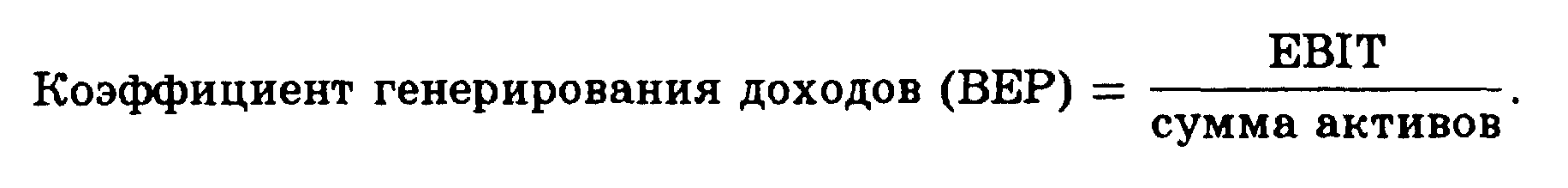
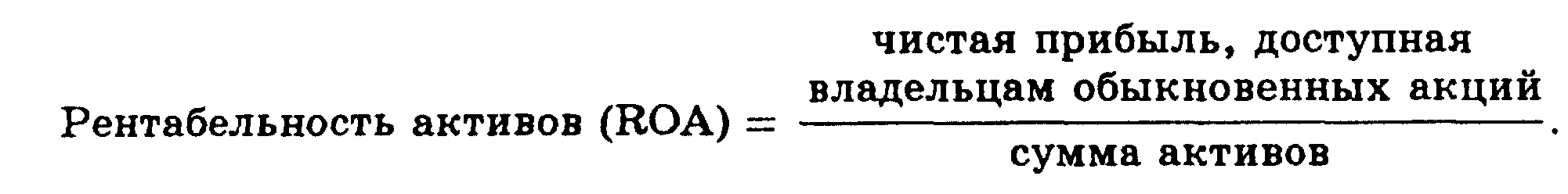
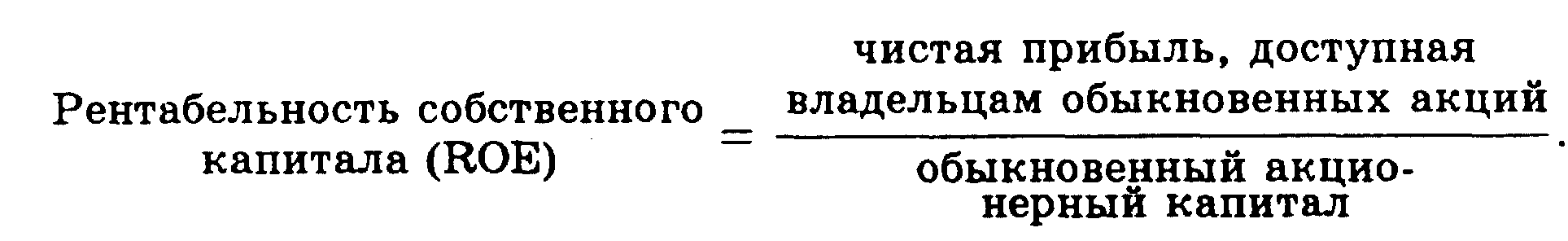
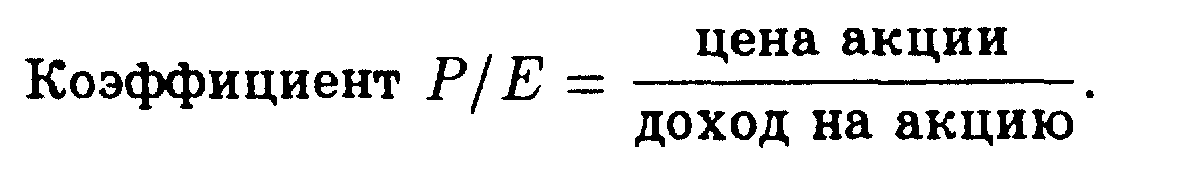
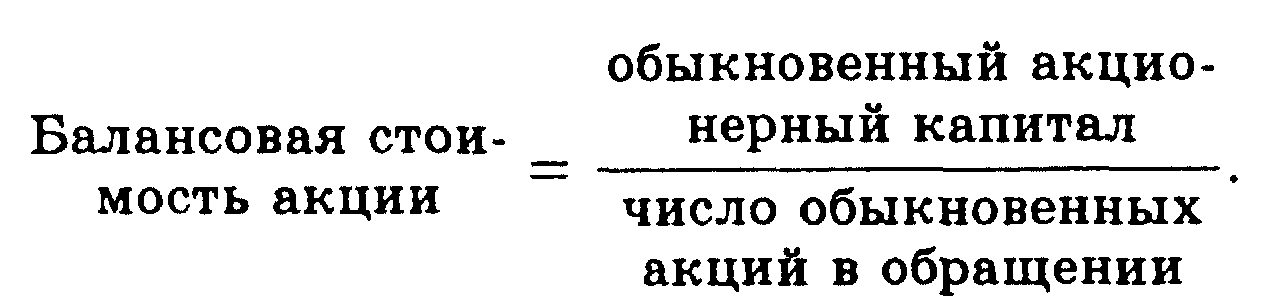
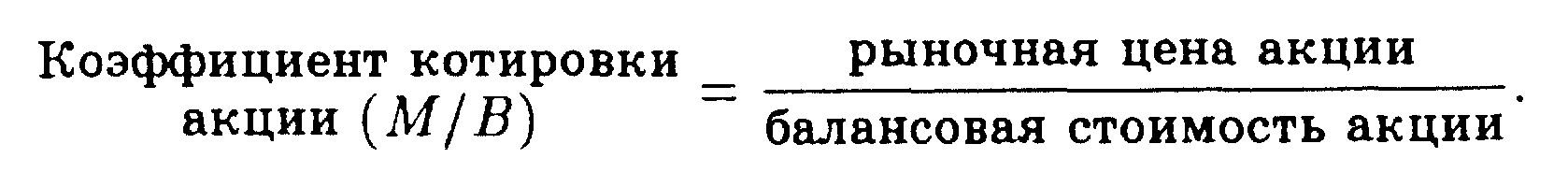
Тема 5.

Временная стоимость денег


План лекции

1. Введение

2. Математическое дисконтирование денежных потоков

3. Полугодовой и другие периоды компаундирования

4. Виды процентных ставок

5. Непрерывное компаундирование и дисконтирование

6. Потоки платежей

6.1. Виды потоков платежей и их основные параметры

6.2. Будущая стоимость ренты

6.2.1. Обычная рента

6.2.2. Вексельная рента

6.3. Текущая стоимость ренты

6.2.1. Обычная рента

6.2.2. Вексельная рента

6.4. Бессрочная рента

6.5. Несколько упрощенных способов вывода формул расчета денежных потоков

7. Неравномерное движение потока наличности

7.1. Текущая стоимость неравномерных денежных потоков

7.2. Будущая стоимость неравномерных денежных потоков

7.3. Определение “i” неравномерных денежных потоков

8. Амортизационные кредиты

9. Сколько стоит фирма?

Дополнительные проблемы


Литература:

1. Брігхем Е. Основи фінансового менеджменту: Пер. з англ. – К.: Молодь, 1997.- 1000 с.
   
2. Brigham E., Gapenski D. Financial Management: Theory and Practice. -New York, The Dryden Press, 1991.
   
3. Corporate Finance, S.Ross, R.Westerfield and J.Jaff 4/e 1996.- 560 pp.
   
4. Foundamentals of Corporate Finance, 4/e S.Ross, R.Westerfield and B.Jordan 1997.- 720 pp.
   
5. Student Problem Manual for use with Corporate Finance, S.Ross, R.Westerfield and J.Jaff /Prepared by Robert C.Hanson 1996.- 352 pp.
   
6. Instructor's Manual to accompany Corporate Finance, S.Ross, R.Westerfield and J.Jaff/Prepared by Kirt C.Butler 1996.-235 pp.
   
7. Student Problem Manual for use with Corporate Finance, S.Ross, R.Westerfield and J.Jaff /Prepared by Thomas H.Eyssell 1995.-287 pp.
   

Введение

Эта лекция посвящена стоимости денег во времени и чистой текущей стоимости. NPV зависит от размера, времени и возможного риска ожидаемых денежных потоков. Для того, чтобы фокусироваться на стоимости денег во времени, мы принимаем совершенную уверенность в будущих денежных потоках в этой лекции. Риск вводится в более поздних лекциях.

Способы определения NPV

Есть четыре пути, чтобы определить NPV: с финансовым калькулятором, с формулами, с компьютером, и с таблицами фактора стоимости денег во времени. Мы настаиваем, что все студенты понимают формулы стоимости денег во времени и могут выполнить алгебру компаундирования и дисконтирования. Это существенно для того, чтобы отчетливо представлять себе денежные потоки и необходимо, чтобы оценить большие комплексные денежные потоки при рассмотрении последующих лекций.


Рецепт для принятия NPV решений

Мы начинаем изучение этой темы с помощью следующего способа. Шаги в этом способе NPV особенно полезны в комплексных проблемах оценки.

1. Распознайте размер, и расписание всех релевантных денежных потоков на линии времени.

2. Распознайте риск и дисконтную ставку, которая применяется к денежному потоку.

3. Вычислите чистую текущую стоимость (NPV) с помощью дисконтирования денежных потоков в соответствии с дисконтной ставкой.

4. Сравните стоимость конкурентных потоков CF в одной и той же точке времени.


Последний шаг есть напоминание, что мы должны сравнивать яблоки с яблоками. Сравнение денежных потоков в двух различных точках времени без поправки на стоимость денег во времени подобно сравнению яблок с апельсинами.


2. Математическое дисконтирование денежных потоков

Алгебра дисконтированных денежных потоков включает два виды операций. Компаундирование наращивает текущие стоимости в будущее, а дисконтирование приводит будущие стоимости к настоящему времени.


Компаундирование

Предположим, мы инвестируем $ 1 под 9% на два года.


Мы должны представить эту оплату наличными на линии времени, как:




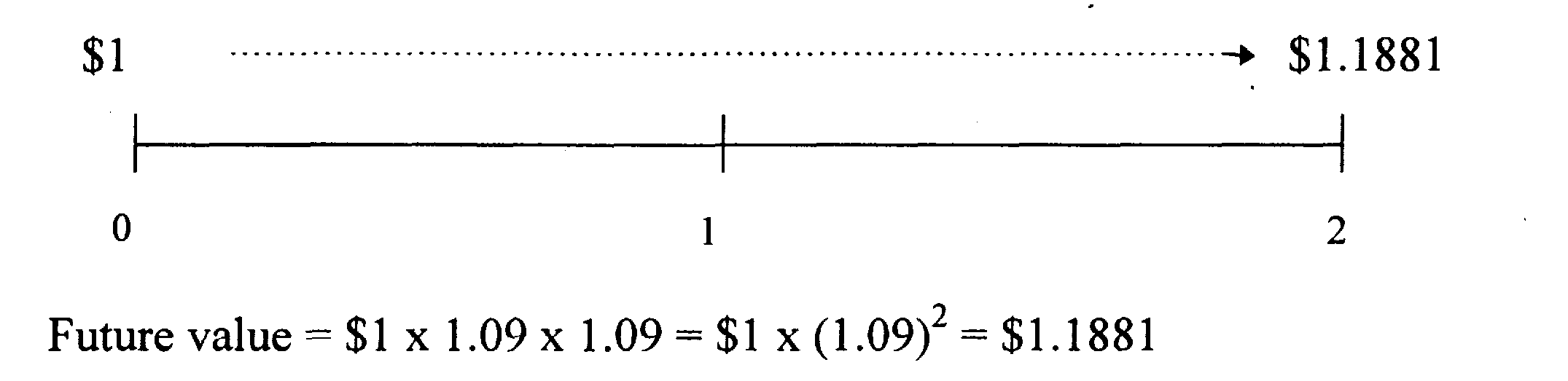
Дисконтирование

Предположим, мы должны получить $1через два года.




Текущая стоимость PV = $1 x (1/1.09) x (1/1.09) = $1 / (1.09)² = $0.842.


Величина 1/(1.09)² называется дисконтный фактор.


Пример расчета будущей стоимости инвестиции в $100 под 10% годовых сроком на 5 лет представлен в таблице и на диаграмме ниже.









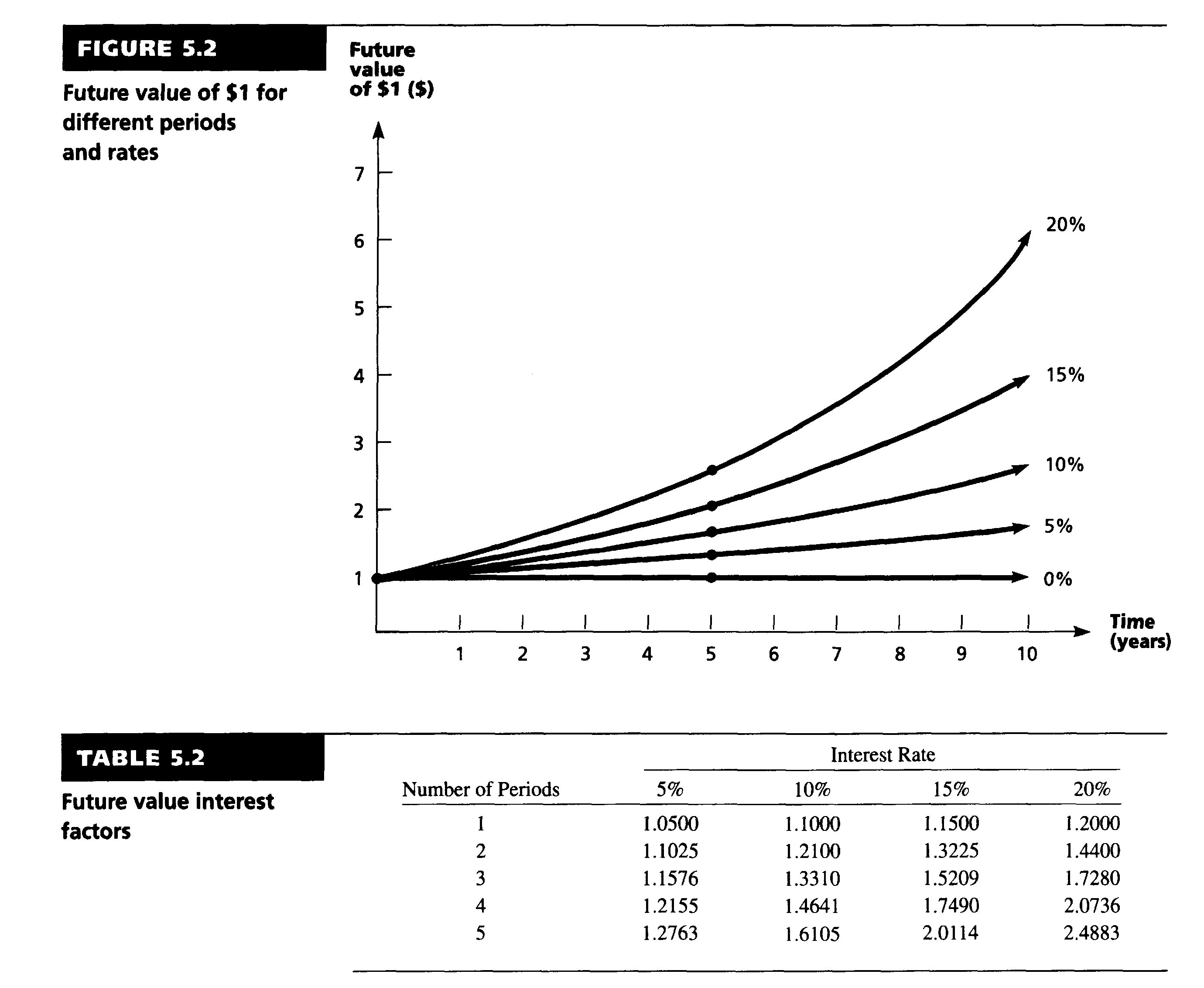
Будущая стоимость $1 при разных ставках процентов представлены в таблице и на диаграмме ниже


Текущая стоимость $1 при разных ставках процентов представлена в таблице и на диаграмме ниже






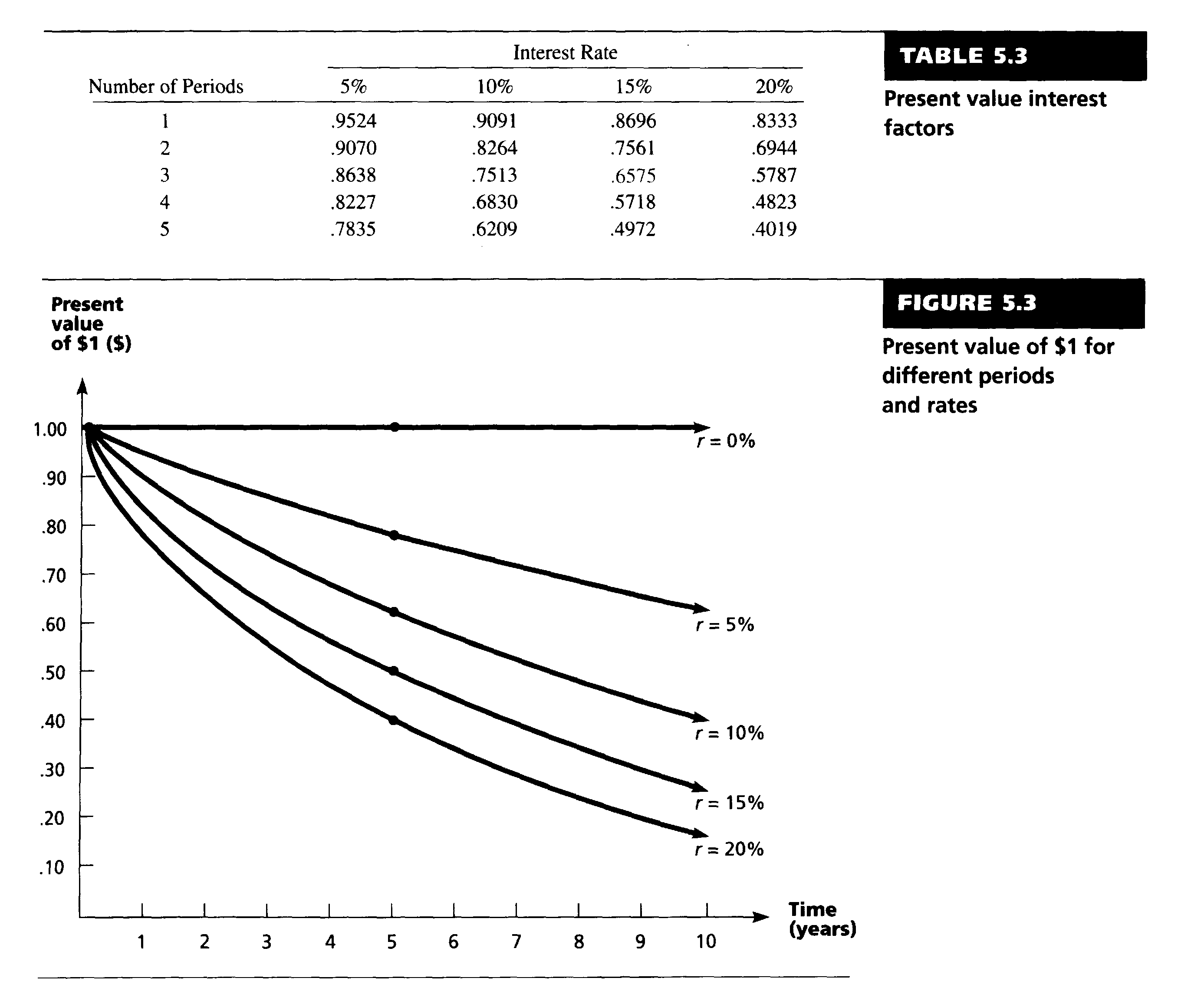
3. Полугодовой и другие периоды компаундирования

Годовое компаундирование: арифметический процесс определения конечной стоимости одного или серии потоков наличности с прибавлением процентной ставки в конце года.

Полугодовое компаундирование: арифметический процесс определения конечной стоимости одного или серии потоков пленки с прибавлением процентной ставки дважды на год.


Полугодовое компаундирование

К этому времени во всех наших примерах мы выходили из того, что процесс компаундирование имеет место раз в год. Такой процесс называется годовым компаундированием. Но вообразите такую ситуацию: Вы положили в банк $100. Банк обязывается платить Вам 6% годовых, но платиться они будут каждые полгода. Такой процесс называется полугодовым компаундированием. Сколько Вы получите в конце первого года, двух лет и любые другие периоды при условии полугодового компаундирования?

Для того, чтобы проиллюстрировать процесс полугодового компаундирования, припустим, что $100 положены на банковский счет на 3 года под 6% годовых. Для начала давайте еще раз рассмотрим, что происходит при годовом компаундировании:

1. Часовая линия, уравнение, числовое решение




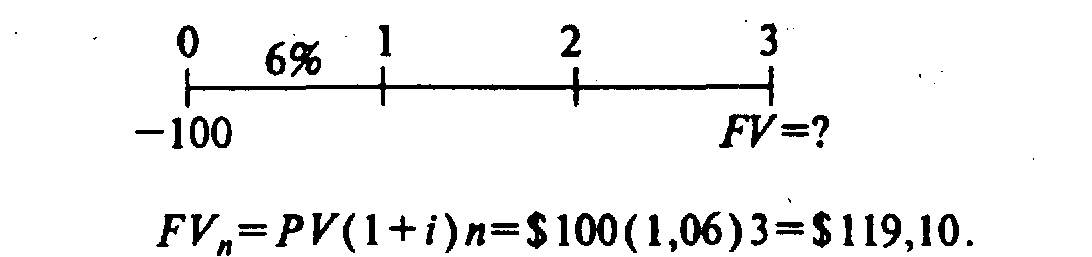
FVn=PV (1+i) ⁿ =$100 (1.06) ³ = $119,10


Но в случае, что нами рассматривается, банк платит проценты неоднократно в течение года. И вообще, например, по облигациям проценты, конечно, платятся раз на полгода, по многим ценным бумагам раз в квартал, по залогам и различного рода кредитам - ежемесячно. Поэтому для Вас очень важно понять, как действует не годовое компаундирование. Если выплаты осуществляются неоднократно на год, а чаще, или если компаундирование процентов осуществляется чаще, чем раз в год. Вам необходимо перевести показатель условно принятой процентной ставки в "периодическую ставку", а количество лет в "количество периодов", как это показано ниже:


Периодическая ставка = Определенная процентная ставка / Количество выплат на год

Число периодов = Число лет * Число периодов на год


В нашем примере, в котором мы должны определить стоимость 100 долларов США по окончании 3 лет при условно принятой процентной ставке в 6 процентов и при полугодовом компаундировании (или дважды на год) Вам следует начать со следующего:

Периодическая ставка =6% / 2=3%.

Периоды = N =• З * 2 = 6.

При данных условиях каждые 6 месяцев в течение 6 периодов на взнос будет начисляться по 3 процента, а не 6 процентов за 3 года. Как мы увидим ниже, между этими двумя процессами существует значительная разница.

Изменения следует сделать перед началом работы над задачей, поскольку все расчеты должны осуществляться на основании показателей количества периодов и периодической ставки, а не количества лет и определенной процентной ставки. Эти же показатели используются при разрешении задач при помощи часовой линии и финансового калькулятора.

Выполняя необходимые изменения, мы сможем определить стоимость 100 долларов США, вложенных на счет под 6 процентов с полугодовым компаундированием, по окончании 3 лет. Часовая линия для данного примера будет выглядеть таким образом:





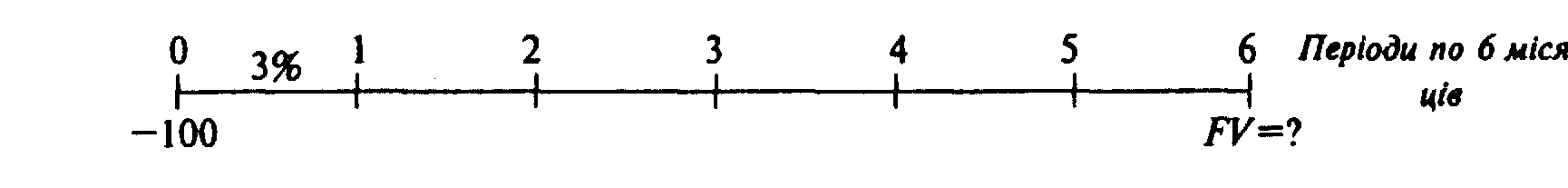
1. Уравнение и числовое решение:

FVn = PV (1+i) ⁿ =$100 (1.03) ⁶ =$100 (1,1941) = $119,41

где i ставка за период = годовой ставке/количество периодов на год=6% / 2=3%,

п общее число периодов = годы * периоды на год = З * 2 = 6.

4. Виды процентных ставок

Эффективная (эквивалентная) процентная ставка (EAR или EFF%) в годовом исчислении может быть определена как ставка, при которой будущая стоимость взноса будет такой же, как при годовому компаундировании.

Процентная ставка в годовом исчислении (АРR): периодическая ставка, умноженная на количество периодов на год.


Эффективная (эквивалентная) процентная ставка (EAR или EFF%)

По банковским счетам, например, проценты начисляются ежедневно, по большинству видов облигаций - раз на полугодие, по акциям - ежеквартально. Для того, чтобы сравнивать ценные бумаги с различными периодами компаундирования необходимо перевести их на общую основу. Для этого мы должны четко понимать разницу между номинальными (или котировочними) процентными ставками и эффективными (или эквивалентными) процентными ставками в годовом исчислении.

Номинальная или котировочная ставка в нашем примере равна 6%. Эффективная или эквивалентная процентная ставка в годовом исчислении может быть определена как ставка, при которой будущая стоимость взноса будет такой же, как при годовом компаундировании. В нашем примере эффективная процентная ставка - это ставка, при которой по окончании трех лет FV инвестированной суммы будет 119,41 долларов США.

Определить эффективную процентную ставку в годовом исчислении можно при помощи ниже приведенного уравнения, если мы имеем показатели номинальной ставки и количество периодов компаундирования:

Эффективная ставка = EAR (или EFF% = [1+(inom / m)] ^m- 1


Пример Например, для того, чтобы вычислить эффективную процентную ставку в годовом исчислении при номинальной ставке 6% и полугодовому компаундировании, нам нужно решить такое равнение:

ЕАR = (1 + 0.06 / 2) ² - 1,0 = (1.03)² - 1,0 = 0,0609 = 6,09%.

То, что мы узнали о полугодовое компаундировании, может быть обобщено таким образом: если компаундирование проводится чаще, чем раз в год, то для определения будущей стоимости любой теперешней суммы мы можем пользоваться более простой версией уравнения 6-1:

Годовое компаундирование: FVn =PV (1+i)ⁿ

Более частое компаундирование FVn =PV [1+(inom / m)] ^mn


Процентная ставка в годовом исчислении

Пример Рассмотрим проценты, которые начисляются по кредитным карточкам. Большинство банков в этом случае предлагают 1,5 процента ежемесячно и в своих рекламных проспектах обещают процентную ставку в годовом исчислении (АРR) в размере 18,0%.

Однако, "реальной" будет эффективная ставка в годовом исчислении, какая равняется 19,6%



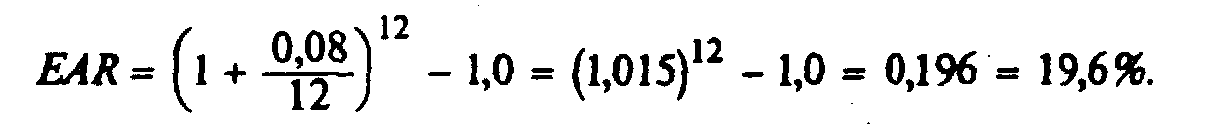
Полугодовые и другие периоды компаундирования могут быть также использованы для дисконтирования, как одновременных выплат, так и рент.

Пример Для начала рассмотрим пример, в котором мы хотим определить размер РV обычной ренты (сумма 100 долларов США) по окончании трех лет при процентной ставке в 8 процентов и годовому компаундировании:

Часовая линия:



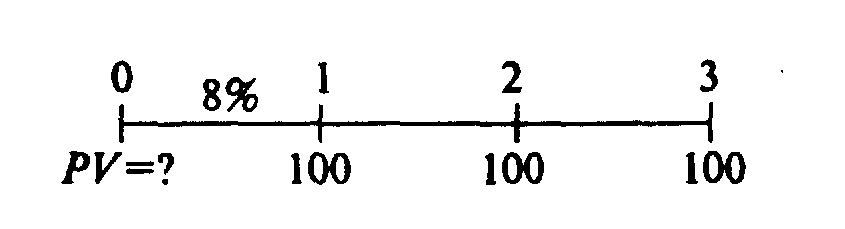
1. Числовое решение:

Рассчитайте РV каждого отдельного потока наличности и подытожите их. РV ренты будет 257,71 долларов США.

2. Решение при помощи финансового калькулятора:

Вводим данные: Результат:

N 6, I 8, РМТ 100, FV 0, РV =-257,71


Пример А теперь давайте попробуем изменить ситуацию. Например, рассмотрим пример для ренты с выплатой $50 ежемесячно, а не $100 на год, при 8-процентной ставке и полугодовом компаундировании. Часовая линия будет выглядеть таким образом:




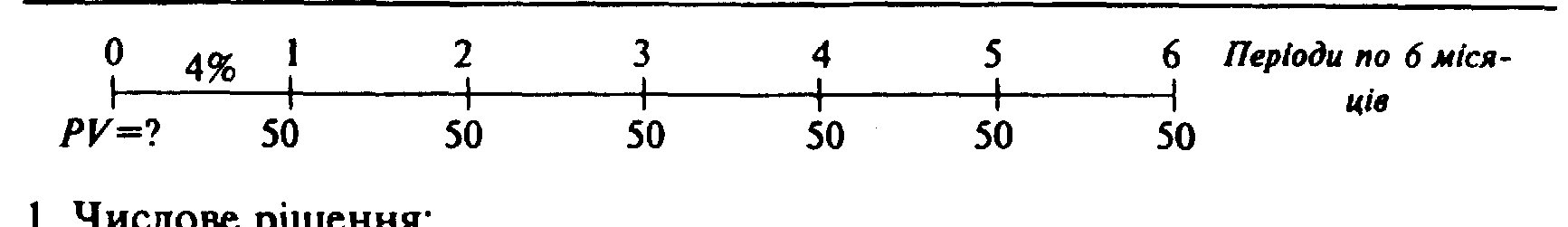
Числовое решение:

Определите РV каждого отдельного потока наличности при помощи 4-процентного дисконтирования. Каждый штрих на часовой линии значит период, так что в нашем случае их 6. РV ренты -262,11 долларов США. Вспомните, что при годовом компаундировании этот показатель был 257,71.

Как видим, 50-долларовая рента с полугодовыми выплатами более выгодная, чем 100-долларовая годовая.

Вопросы для самопроверки

Какие изменения Вы должны внести в расчеты для определения будущей стоимости суммы, которая будет компаундироваться на 8 процентов раз на полугодие, в отличие от расчетов для годового компаундирования при такой же процентной ставке?

Почему с точки зрения инвестора полугодовое компаундирование лучше за годовое?

Что значат термины "процентная ставка в годовом исчислении", "эффективная процентная ставка", "номинальная процентная ставка"?

рассмотрим заем финансовой компании под 3 процента ежеквартально:

таким образом (6-8):

5. Непрерывное компаундирование и дисконтирование

Ранее мы обсуждали только ситуацию, когда процент начисляется через определенные промежутки времени: раз в год, раз на полугодие, раз в месяц, и т. д. У некоторых случаях мы можем столкнуться с немедленным, или непрерывным ростом сумм. В данном случае мы рассмотрим, каким образом проводятся расчеты будущей стоимости, если процентная ставка компаундируется непрерывно.

Непрерывное компаундирование

Непрерывное компаундирование: ситуация, при которой процент прибавляется непрерывно, а не в определенные моменты времени.


Соотношение между дискретным и непрерывным компаундированием может быть проиллюстрировано на графике 6А-1. График А иллюстрирует годовое компаундирование, при котором процент начисляется раз в год; график Б отображает ситуацию, при которой компаундирование проводится дважды на год; график В отображает процесс непрерывного начисления процента. Как видно с кривых графика, чем меньший период компаундирования, тем больший конечный результат. Это происходит потому, что в этом случае процент на процент начисляется чаще.

Уравнение, данное ниже, может применяться для расчета любого количества периодов компаундирования на год. Компаундирование, которое проводится чаще, чем раз в год:

FVn =PV [1+(inom / m)] ^mn

Для иллюстрации, припустим, что мы имеем такие данные: PV=$100, i=10%, n=5. При различных периодах компаундирования мы получим следующие показатели будущей стоимости по окончании 5 лет:

Годовое: РV = $100 [1+(0.10 / 1)] ^1*5 = $100(1,10)⁵ = $161,05.





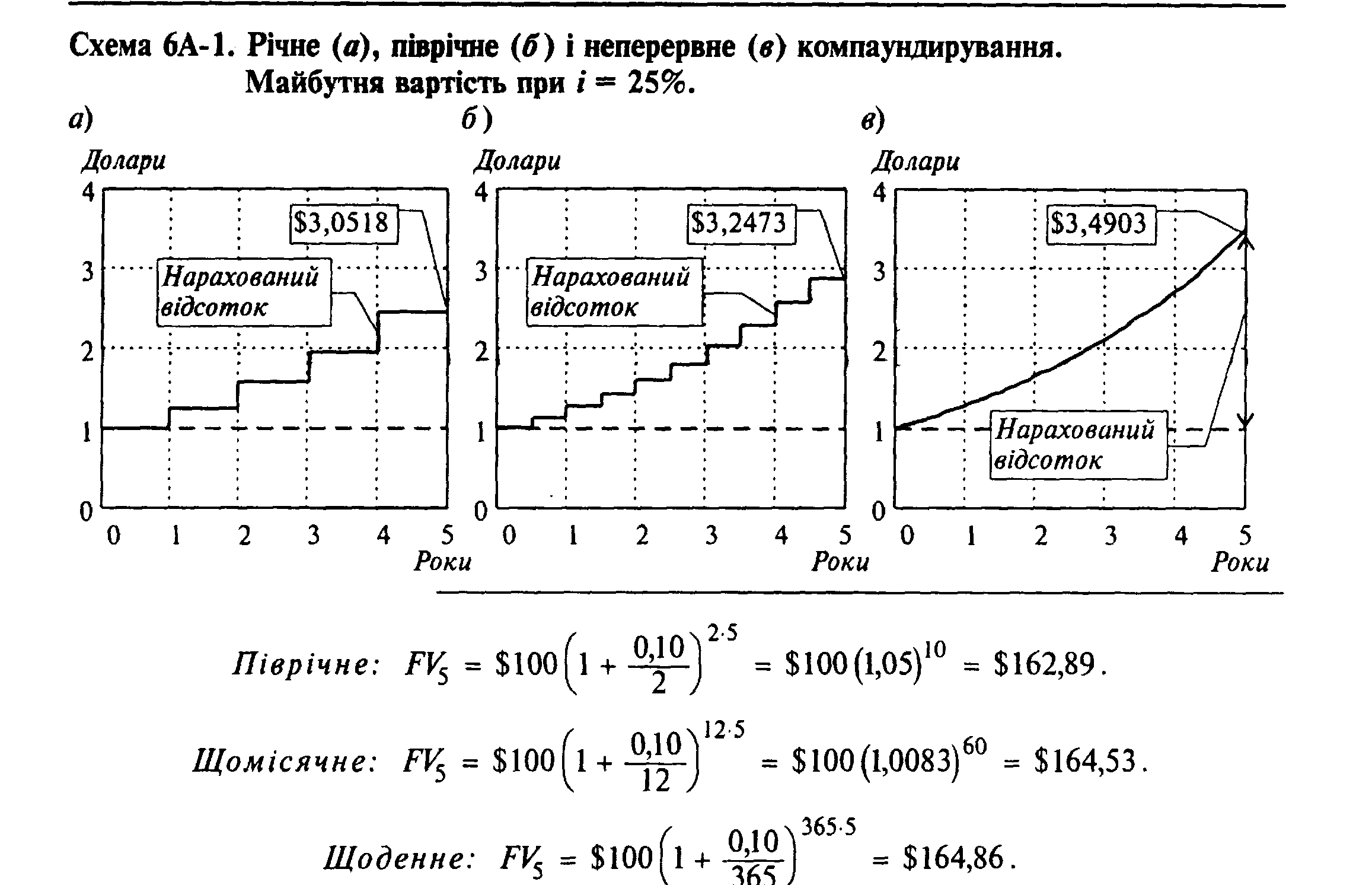
Мы могли бы продолжать рассчитывать FV для периодов компаундирования раз в час, раз в минуту, раз на секунду и т.д., до того, как дошли бы до компаундирования, которое проводится непрерывно. Уравнение для такого типа компаундирования такое:

FVn =PV (e ⁱⁿ) (3.5-1)

Здесь е имеет значение 2,7183.

Пример При взносе в 100 дол. США на 5 лет при 10-процентном непрерывном компаундировании FV может быть рассчитано таким образом:

Непрерывное: FV5 =$100(e ^0.10*5) = $100 (2,7183…) ^0.10*5 = $164,87


Для применения уравнения (6А-1) можно использовать калькуляторы с экспоненциальными функциями. Например, с калькулятором НР-100В Вы вводите .5, потом нажимаете клавишу e^х для получения 1,6487 и умножаете на $ 100, чтобы получить $ 164,87.


Непрерывное дисконтирование

Уравнение 3.5-1 может быть трансформировано в равнение 3.5-2 и применено для определения текущей стоимости при непрерывном дисконтировании:

PV = FVn / (e ⁱⁿ )= FVn / (e ^-in) (3.5-2)

Пример Таким образом, если известно, что через 10 лет некоторая сумма вырастет до $1649 при условии применения непрерывной дисконтной ставки i = 5, текущая стоимость платежа с такой будущей стоимостью будет составлять:

PV =$1,649 / (e^0,5) = $1,649 / $1,649 = $1,000

Вывод формул

Будущая стоимость денежных потоки Co в конце лет T с непрерывным компаундированием при установленной ежегодной процентной ставке r может быть найдена с помощью нахождения предела эффективной ежегодной процентной ставки из формулы (1+R) = (1+(r/m)) ^m , при m => oo:


Lim m=>oo (l+fr/m)) ^m = e ^r.


Компаундирование за период T, дает результат (1+r) ^Т = (e ^r) ^Т = e ^rТ.

Замена этим значением внутри уравнения будущей стоимости FV = Co (1+R)^Т дает формулу вычисления будущей стоимости при непрерывном компаундировании за период владения:



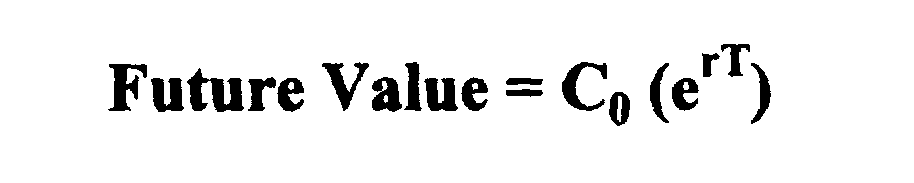
Соответственно, при непрерывном компаудировании, текущая стоимость будущих денежных потоков, которая получается ко времени T является



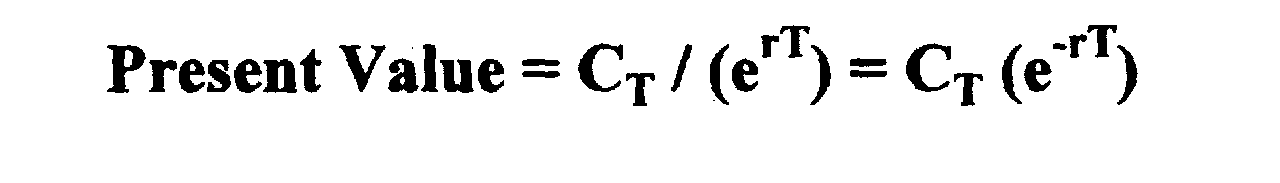
Число e есть постоянное и приблизительно равно 2.718.


6. Потоки платежей

6. 1. Виды потоков платежей и их основные параметры

Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени. Например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т. д. Такие последовательности, или ряды, платежей назовем потоком платежей. Заметим, что в западной финансовой литературе в аналогичном смысле применяется термин "cash flows" (буквально — потоки наличности). Отдельный элемент этого ряда назовем членом потока.

Классификация потоков.

Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а соответствующие платежи могут производиться через разные интервалы времени.

Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой, или просто рентой, а иногда аннуитетом (annuity) независимо от назначения или происхождения платежей. Например, рентой являются последовательность получения процентов по облигации, платежи по потребительскому кредиту, выплаты в рассрочку страховых премий и т. д. Как видим, во всех приведенных случаях выплаты или получения денег производятся через равные промежутки времени. Использование в финансово-банковской операции условий, предполагающих выплаты в виде финансовой ренты, существенно упрощает количественный их анализ, дает возможность применять стандартные формулы и таблицы значений ряда необходимых для расчетов коэффициентов и быстро выполнять расчеты на калькуляторах.

Рента характеризуется следующими параметрами: член ренты (rent) — размер отдельного платежа, период ренты (rent period, payment period) — временной интервал между двумя последовательными платежами, срок ренты (term) — время от начала первого пери­ода ренты до конца последнего периода, процентная ставка. Размер ставки не всегда прямо оговаривается в условиях финансовой ренты, вместе с тем этот параметр крайне необходим для се анализа.

При характеристике отдельных видов рент необходимы дополнительные условия и параметры: число платежей в году, способ и частота начислений процентов.

В практике применяют разные по своим условиям ренты. В основу их классификации могут быть положены различные признаки. Рассмотрим некоторые из таких классификаций.

По количеству выплат членов ренты на протяжении года ренты делятся на годовые (выплата раз в году) и р-срочные (р — количество выплат в году). В анализе производственных инвестиционных процессов иногда применяют ренты с периодами, превышающими год. Перечисленные виды рент называют дискретными. В финансовой практике встречаются и с такими последовательностями платежей, которые производятся столь часто, что их практически можно рассматривать как непрерывные.

По количеству начислений процентов на протяжении года различают: ренты с ежегодным начислением, с начислением т раз в году, с непрерывным начислением. Моменты начисления процентов необязательно совпадают с моментами выплат членов ренты. Однако, как будет показано, расчеты заметно упрощаются, если два указанных момента совпадают.

По величине своих членов ренты делятся на постоянные (с одинаковыми платежами) и переменные. Члены переменных рент изменяют свои размеры во времени, следуя какому-либо закону, например арифметической или геометрической прогрессии, либо несистематично (задаются таблицей).

По вероятности выплат ренты делятся на верные (annuity certain) и условные (contingent annuity). Верные ренты подлежат безусловной уплате, например при погашении кредита. Число членов такой ренты заранее известно. В свою очередь выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. К такого рода рентам относятся страховые аннуитеты — различные последовательные платежи в имущественном и личном страховании. Типичным примером страхового аннуитета является пожизненная выплата пенсии.

По количеству членов различают ренты с конечным числом членов, т. е. ограниченные по срокам ренты (их срок заранее оговорен), и бесконечные, или вечные, ренты (perpetuity). С вечной рентой встречаются на практике в ряде долгосрочных операций, когда предполагается, что период функционирования анализируемой системы или срок операции весьма продолжителен и не оговаривается конкретными датами. В качестве вечной ренты логично рассматривать и выплаты процентов по облигационным займам с неограниченными сроками.

По соотношению начала срока ренты и какого-либо момента времени, упреждающего начало ренты (например, начало действия контракта или дата его заключения), ренты делятся на немедленные и отложенные, или отсроченные (deffered annuity).

Очень важным является различие рент по моменту выплат платежей в пределах периода. Если платежи осуществляются в конце периодов, то соответствующие ренты называют обыкновенными, или постнумерандо (ordinary annuity), если же платежи производятся в начале периодов, то их называют вексельными или пренумерандо (annuity due). Иногда контракты предусматривают платежи или поступления денег в середине периодов.

Приведем пример. Контракт предусматривает периодическое погашение задолженности выплатой в конце каждого полугодия одинаковых погасительных платежей на протяжении фиксированного числа лет. Таким образом, предусматривается постоянная, полугодовая, верная, ограниченная рента постнумерандо. Если первая выплата в счет погашения основной суммы долга производится спустя, скажем, два года после подписания контракта (льготный период), то эта рента является отложенной относительно даты заключения договора.

Обобщающие параметры потоков платежей. В подавляющем числе практических случаев анализ потока платежей предполагает расчет одной из двух обобщающих характеристик: наращенной суммы или современной стоимости. Наращенная сумма (amount of cash flows) — сумма всех членов потока платежей с начисленными на них к концу срока процентами. Под современной стоимостью потока платежей (present value of cash flows) понимают сумму всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.

6.2. Будущая стоимость ренты

6.2.1. Обычная рента

Рента: это серия выплат равных сумм, которые осуществляются через определенные интервалы или определенное количество периодов.

Обычная (отсроченная) рента: рента, выплаты по которой осуществляются в конце каждого периода.

Вексельная рента: рента, выплаты по которой осуществляются в начале каждого периода.


Обычная, или отсроченная рента состоит из серии равных выплат, которые осуществляются в конце каждого периода. Если Вы будете класть на депозит, на трехгодичный срок по $100 в конце каждого года под 5% годовых, какую сумму Вы будете иметь по окончании 3 лет? Для ответа на этот вопрос мы должны рассчитать будущую стоимость ренты, FVAn.

Осуществляется начисление платежа на платеж до конца п-го периода. Сумма

этих платежей и является будущей стоимостью аннуитета, FVAn. Часовая линия:



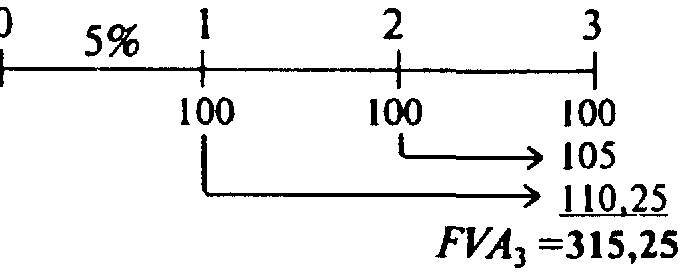
В данном случае верхняя часть диаграммы выражает собой обычную часовую линию, а в нижней части показывается, как компаундируется каждый поток наличности для того, чтобы получить значение FVAn.

Уравнение:



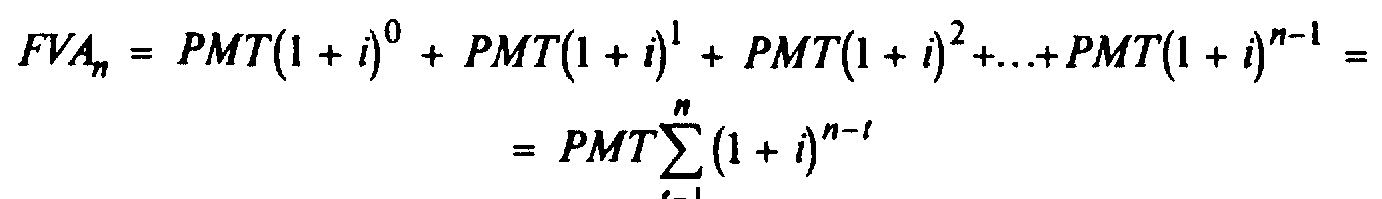
Обратите внимание на то, что первая строка уравнения отображает рентные выплаты в противоположном порядке. Вследствие того, что первая выплата осуществляется в конце первого периода, процент платится уже во втором периоде. Таким образом, компаундирование будет осуществляться не для периода n, а для периода n -1 и т. д. Последняя выплата осуществляется в самом конце, поэтому проценты по ней не начисляются.

1. Числовое решение.

Нижняя часть часовой линии показывает числовое решение. Рассчитывается будущая стоимость каждого потока наличности отдельно. Потом результаты прибавляются, и в итоге мы получаем будущую стоимость ренты $315,25. Этот метод очень трудоемкий и неэффективный.

2. Решение при помощи таблиц.

Процентная часть уравнения называется фактором процента будущей стоимости ренты (FVIFAi,n)*:



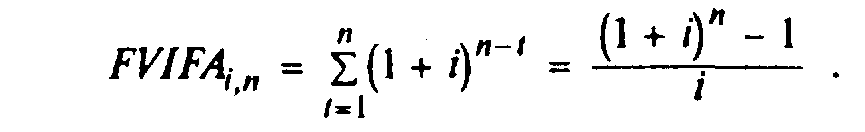
* Третья часть равнения решается при помощи арифметических и геометрических прогрессий. Данное уравнение очень удобное для ситуаций, когда нужны значения i и n, которые не поданы в таблице и под рукой нет финансового калькулятора.

Фактор процента будущей стоимости аннуитета ( FVIFAi,n) - фактор процента будущей стоимости для аннуитета за n периодов и с i процентной ставкой. Значение FVIFA уже высчитано для различных комбинаций i и n, много из которых внесено в таблицу А-4 (см. дополнение А). Для того, чтобы найти ответ (припустим, для 100 долларовой США трехгодовой ренты), следует сначала обратиться к таблице А-4 и посмотреть столбик для 5% для третьего периода. Ответ будет: FVIFA=3,1525. Таким образом, мы теперь знаем, что будущая стоимость 100-долларовой ренты будет $315,25:

FVA=РМТ (FVIFAi,n)

FVAз=$100(FVIFA5%,3) =$100 (3.1525) = $315,25.

3. Решение при помощи финансового калькулятора.

Вводим данные: Результат:

N 3, I 5, РV 0, РМТ -100, FV =315,25


Отметьте, что при решении задач, которые относятся к ренте, кнопка РМТ используется в совокупности с кнопками N и I, плюс или кнопка РV, или FV, в зависимости от того, какое значение ренты Вы хотите узнать: РV, или FV. В нашем примере нам необходимо вычислить FV. Поэтому мы нажимаем соответствующую кнопку. В результате получим ответ: $315,25. РV в нашем случае равно нолю.


6.2.2. Вексельная рента

Если бы три платежа по $100 каждый были осуществлены в начале каждого года, тогда аннуитет (рента) стал бы вексельной рентой. В числовом формате каждый платеж будет смещен влево на один год, поэтому на каждый платеж будут начислять проценты дополнительно за один дополнительный год.

1. Числовой формат и числовое решение.



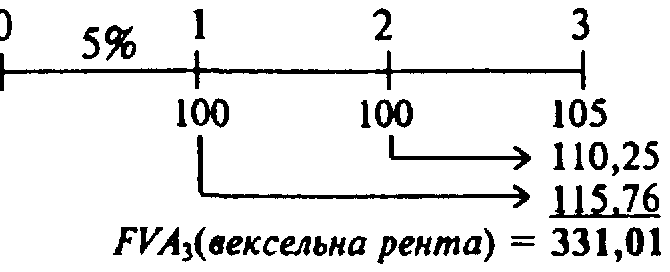
Снова обычный числовой формат показан в верхней части диаграммы, данные, полученные при помощи калькулятора, отмеченные под годом.

2. Решение при помощи таблиц.

При вексельной ренте на каждый платеж начисляются проценты за один дополнительный период, поэтому будущая стоимость всего аннуитета (ренты) равно будущей стоимости обычного аннуитета, умноженной на дополнительное начисление процентов за один дополнительный период. Приводим решение c помощью таблиц:

FVAn =РМТ (FVIFAi,n)

FVAз=$100(FVIFA5%,3) =$100 (3.1525) (1.05) = $331,01.


Платежи осуществляются раньше, поэтому больше зарабатывается процентов. Вследствие чего будущая стоимость вексельной ренты больше - $331,01 в сравнении с $315,25 для обычного аннуитета.

3. Решение при помощи финансового калькулятора

Большинство финансовых калькуляторов имеют переключатель, обозначен DUE или BEGIN, что позволяет Вам переключиться от платежей в конце периода (обычный аннуитет) к платежам на начало периода (вексельная рента). Когда начальная система активизируемая, дисплей показывает слово "BEGIN". Таким образом, для разрешения задачи, связанной с вексельной рентой, нужно переключить Ваш калькулятор в BEGIN и выполнять операции, как и раньше.

BEGIN

Вводим данные: Результат:

N 3, I 5, РV 0, РМТ -100, FV = 331,01

Вводим: N=3, I=5, PV =О, РМТ= - 100 и нажимаем FV для получения ответа $331,01. Из-за того что большинство задач имеют СF в конце периода, Вам всегда следует переключать Ваш калькулятор назад к END после Вашей работы с вексельной рентой.

Вопросы для самопроверки

Какая разница между обычной и вексельной рентой?

Как нужно изменить уравнение для определения обычной ренты с тем, чтобы его можно было применить для расчета вексельной ренты?

Разъясните, как нужно пользоваться финансовым калькулятором для расчета будущей стоимости ренты.

•6.3. Текущая стоимость ренты

6.3.1. Обычная рента

Припустим, что Вам предложен такой выбор: 1) трехгодовая рента с выплатой 100 долларов США в конце каждого года и 2) одноразовая выплата всей суммы сегодня же.

В следующие три года эти деньги Вам не понадобятся. Поэтому, если Вы выбираете ренту, то можете положить сумму на сберегательный счет под 5 процентов годовых. Одноразовая сумма также может быть положена в банк на точно такой же счет. Какой должна быть сумма одноразовой выплаты, полученной Вами сейчас, чтобы она была величиной, эквивалентной ренте? Решение смотрите ниже.

Часовая линия:




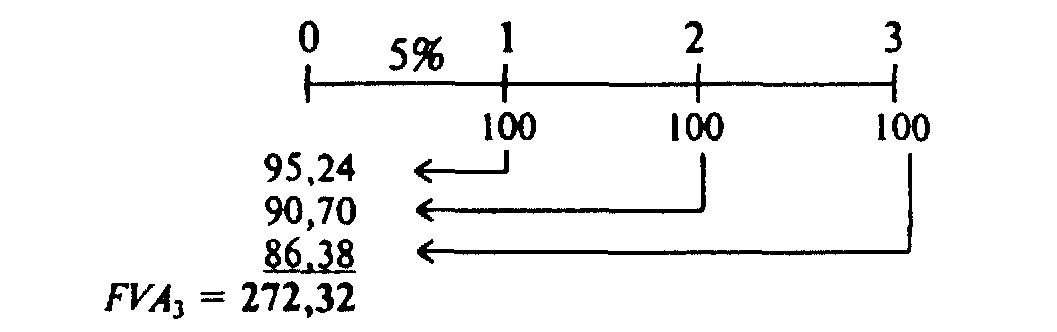
Обычная часовая линия составляет верхнюю часть диаграммы, числовое решение представлено в левом столбике. РV ренты, РVАn в нашем примере будет 272,32 доллара США.

РVАn - текущая стоимость ренты за n-ый период.

Уравнение:



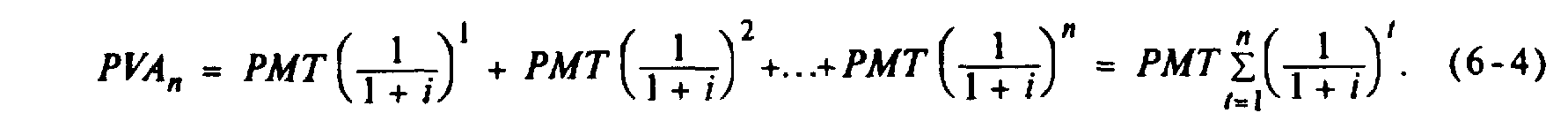
1. Числовое решение

Мы определяем текущую стоимость каждого потока наличности, потом подытоживаем эти показатели и получаем РV ренты. Данная процедура приведена в нижней части диаграммы часовой линии, из которой мы видим, что в нашем случае РV ренты будет 272,32 долларов США.

2. Решение при помощи таблицы

Итоговая сумма уравнения называется фактором процента текущей стоимости ренты (РVIFAi,n). В таблице мы можем найти значение этого показателя для различных n и i. Уравнение будет выглядеть таким образом:

РVAn = РМТ (РVIFAi,n)

Фактор проценту текущей стоимости ренты (РVIFAi,n) - это показатель ренты за n -ное количество периодов, дисконтируемый на i процентов.

Для того, чтобы решить, например, задачу для трехлетней ренты на сумму в 100 долларов США, следует обратиться к таблице А-2 и найти столбик для 5% для третьего периода. Значение (РVIFAi,n) для нашего примера будет 272,32 доллара США, так что мы можем сказать, что текущая стоимость ренты в 100 долларов - 272,32 доллара США.

РVAn = РМТ (РVIFAi,n)

РVAз = =$100 (РVIFA5%,з)=$100 (2,7232) = $272,32.


3. Решение при помощи финансового калькулятора

Вводим данные: Результат:

N 3, 1 5, РУ 0. РМТ -100, РV =272,32


Одним из важнейших аспектов концепции ренты является тот, который связан с кредитами и с постоянными выплатами, такими, как залог имущества, и тому подобное. При таких кредитах, которые называются амортизационными кредитами, взятая под залог сумма является текущей стоимостью обычной ренты, а выплаты составляют поток ренты. Более обстоятельно этот вопрос будет рассмотрен в этом разделе позже.

Итоговая сумма называется РVIFAi,n. Применяя решение при помощи геометрической прогрессии, можно вычислить стоимость:




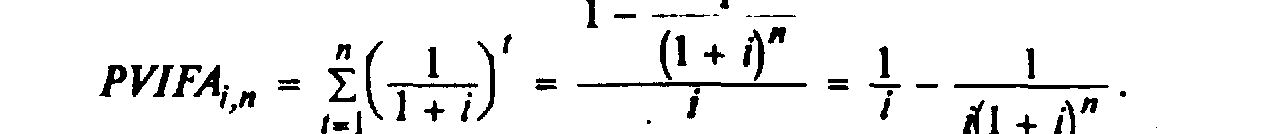
Данная форма равнения очень удобная для определения стоимости ренты, если значение i и n не поданные в таблице и под рукой нет финансового калькулятора.


6.3.2. Вексельная рента

Если бы 100-долларовые выплаты, о которых мы говорили в предыдущем разделе, делались не в конце, а в начале каждого года, то такая рента называлась бы вексельной рентой. Каждый платеж будет смещен влево на один год, поэтому каждый платеж будет дисконтироваться на один год меньше. Приведем пример решения подобного вида задач:

1. Часовая линия и числовое решение:



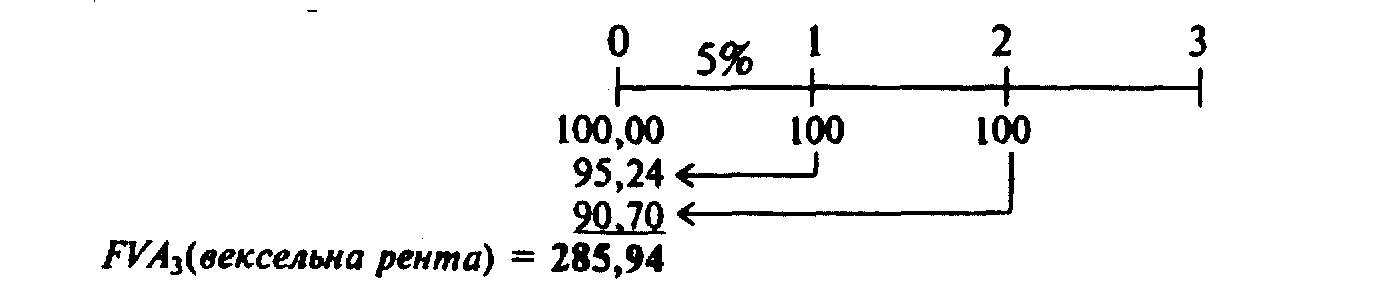
В данном случае мы опять находим РV каждого потока наличности, потом подытоживаем их и получаем РV вексельной ренты. Данная процедура иллюстрируется нижней частью диаграммы часовой линии. Обратите внимание на то, что сумма вексельной ренты большая от величины обычной: 285,94 доллара США против 272,32 доллара США.

2. Решение при помощи таблиц

При вексельной ренте каждый период дисконтируется одной выплатой. Вследствие того, что выплаты выполняются быстрее, вексельная рента имеет большую стоимость, чем обычная, ее значение может быть рассчитано путем умножения показателя РV на (1+i):

РVАn (вексельная рента)=РМТ (РVIFAi,n) (1+i)

= $100 (2,7232) (1,05) = $285,94.

3. Решение при помощи финансового калькулятора

BEGIN

Вводим данные: Результат:

N 3, 1 5, РV В, РМТ -100. РV =285,94


Вопросы для самопроверки

Какая из рент имеет большую текущую стоимость: обычная или вексельная?

Разъясните, как применяется финансовый калькулятор для расчета текущей стоимости ренты?